k-medoidsとは?k-meansとの違いをわかりやすく解説
K-medoidsとは?
K-medoidsは、データをグループ(クラスター)に分割するための教師なし学習アルゴリズムです。

よく知られているK-meansクラスタリングの堅牢な代替手法として位置づけられています。
この手法の基本的な目標は、データポイントを複数のクラスターに分割し、各クラスターが実際のデータポイントから選ばれた代表点(medoid)によって表されるようにすることです。
これがK-meansとの主な違いです。
K-meansではクラスターの中心が仮想的な点(centroid)であるのに対し、K-medoidsではクラスターの代表点が必ず実際のデータポイント(medoid)となります。
medoid
medoidは「中間的な物体」を意味し、クラスター内の他のすべてのポイントとの平均的な非類似度(または距離)が最小となるデータポイントとして定義されます。言い換えれば、medoidはクラスター内の「最も中心的な」ポイントです
K-meansとK-medoidsの違い
k-means含め、他のクラスタリング手法については、こちらをどうぞ
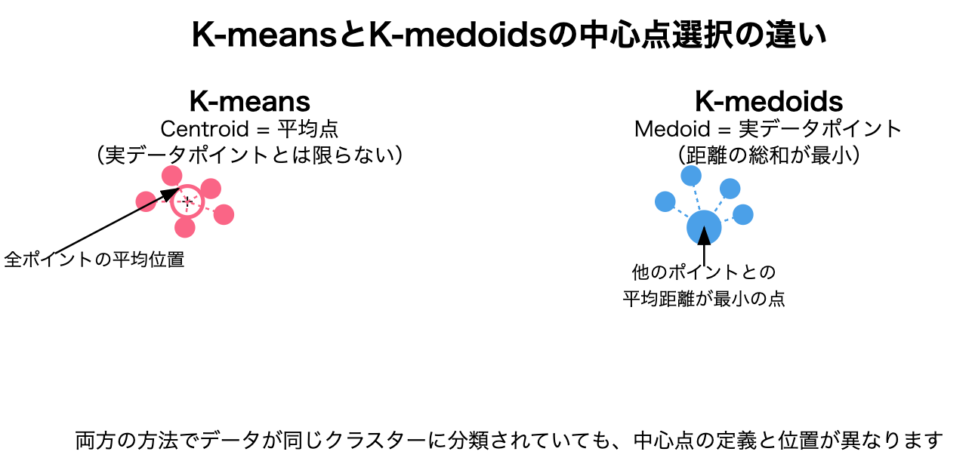
中心点の選び方
K-means
- クラスターの中心は「centroid」と呼ばれ、クラスター内のすべてのポイントの平均として計算されます
- centroidは実際のデータポイントである必要はなく、仮想的な点となることが多いです
K-medoids
- クラスターの中心は「medoid」と呼ばれ、実際のデータポイントから選ばれます
- medoidはクラスター内の他のすべてのポイントとの平均距離が最小となるデータポイントです
距離メトリクスの柔軟性
K-means
- 主にユークリッド距離(L2ノルム)を使用
- 他の距離メトリクスを使うと収束が保証されない場合がある
K-medoids
- 任意の距離または非類似度メトリクスを使用可能
- 以下のような多様なメトリクスに適応できる
メトリクス例
1. ユークリッド距離(L2ノルム)
$${d(x, y) = \sqrt{\sum_{i=1}^{d} (x_i – y_i)^2}}$$
2. マンハッタン距離(L1ノルム)
$${d(x, y) = \sum_{i=1}^{d} |x_i – y_i|}$$
3. コサイン距離
$${d(x, y) = 1 – \frac{x \cdot y}{||x|| \cdot ||y||}}$$
4. ジャッカード距離(カテゴリカルデータ用)
$${d(A, B) = 1 – \frac{|A \cap B|}{|A \cup B|}}$$
選択する距離メトリクスは、データの特性や目的に合わせて選ぶべきです。異なる距離メトリクスは異なるクラスタリング結果をもたらすことがあります。
計算コスト
K-means:
- 計算効率が良い($O(n \cdot k \cdot d \cdot i)$)
- $n$: データポイント数
- $k$: クラスター数
- $d$: 次元数
- $i$: 反復回数
K-medoids:
- 計算コストが高い($O(n^2 \cdot k \cdot i)$)
- 大規模データセットでは効率が悪くなる
→K-medoidsがmedoidの選択において、すべての可能な組み合わせを評価する必要がある
K-medoidsの数学的背景
数学的背景を説明します。
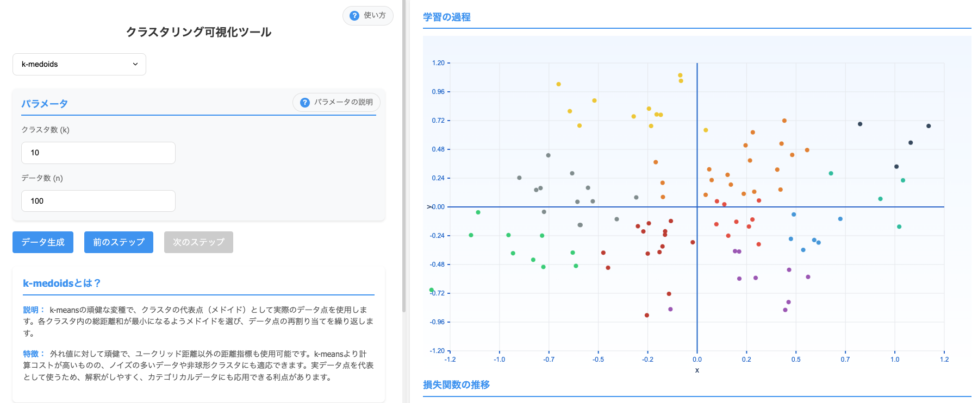
このあたりは、シミュレーションツールを使いながらの方が理解が進みます。
目的関数と最適化問題
K-medoidsの目的関数は、各データポイントからそのクラスターのmedoidまでの距離の総和を最小化することです
$${\min_{M} \sum_{i=1}^{n} \min_{m_j \in M} d(x_i, m_j)}$$
- $M = {m_1, m_2, …, m_k}$はmedoidの集合
- $m_j$
- $j$番目のクラスターのmedoid
- $m_j$
- $d(x_i, m_j)$はデータポイント$x_i$とmedoid $m_j$の間の距離
この最適化問題は、すべての可能なmedoidセットを試すと組み合わせ爆発を起こすため、ヒューリスティックなアプローチを使用して解きます。(下で解説します。)
アルゴリズムのステップ|PAM
K-medoidsにはいくつかの実装バリエーションがありますが、最も一般的なのは「PAM(Partitioning Around Medoids)」と呼ばれるアルゴリズムです。
ステップ1: 初期化
- データセットから$k$個のポイントをランダムに選び、初期medoidとする
- これらの$k$個のポイントを$M = {m_1, m_2, …, m_k}$と表す
ステップ2: 割り当て
- 各データポイント$x_i$を、最も近いmedoidのクラスターに割り当てる
- $x_i$の割り当て先クラスター$C(x_i)$は次のように決定される
$${C(x_i) = \underset{j \in \{1,…,k\}}{\arg\min} \, d(x_i, m_j)}$$
ステップ3: 更新
- 各クラスター$C_j$
- クラスター内の各ポイント$p \in C_j$をmedoid候補と考える
- 各候補$p$について、$p$がmedoidだった場合の総距離を計算
$${T_p = \sum_{x_i \in C_j} d(x_i, p)}$$
- 総距離$T_p$が最小となるポイント$p$を新しいmedoid $m_j$とする
$${m_j = \underset{p \in C_j}{\arg\min} \, T_p}$$
ステップ4: 収束
- medoidが変化しなくなるか、最大反復回数に達するまでステップ2と3を繰り返す
kの選択|シルエットスコア
K-medoidsで適切なクラスター数$k$を選択するために、シルエットスコアを使用することができます。
シルエット分析は、各ポイントについて
- $a(i)$
- ポイント$i$とそのクラスター内の他のすべてのポイントとの平均距離
- $b(i)$
- ポイント$i$と最も近い隣接クラスター内のすべてのポイントとの平均距離
を計算し、シルエットスコア$s(i)$を次のように定義します
$${s(i) = \frac{b(i) – a(i)}{\max(a(i), b(i))}}$$
シルエットスコアの値は-1から1の範囲をとり
- 1に近いほど、ポイントは自身のクラスターに適切に割り当てられている
- 0に近いほど、ポイントは隣接するクラスターとの境界に位置する
- -1に近いほど、ポイントは誤ったクラスターに割り当てられている可能性が高い

全データポイントの平均シルエットスコアが最大となるようなクラスター数$k$を選ぶことが一般的です
K-medoidsの実装例
Pythonを使ってK-medoidsアルゴリズムを実装・適用する例を見ていきましょう。
ここでは、scikit-learn-extraという拡張ライブラリを使用します。
import numpy as np
import matplotlib.pyplot as plt
from sklearn_extra.cluster import KMedoids
from sklearn.datasets import make_blobs
# ランダムなデータセットを生成
X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# K-medoidsモデルを初期化
kmedoids = KMedoids(n_clusters=4, random_state=0)
# モデルをデータに適合させる
kmedoids.fit(X)
# 各データポイントのクラスタラベルを取得
labels = kmedoids.labels_
# medoidのインデックスを取得
medoid_indices = kmedoids.medoid_indices_
# medoidの座標を取得
medoids = kmedoids.cluster_centers_
# 結果を視覚化
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis', alpha=0.8)
plt.scatter(medoids[:, 0], medoids[:, 1], c='red', s=200, marker='*', label='Medoids')
plt.title('K-medoids Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()
# コスト関数の値(総距離の和)を出力
print(f"Total inertia: {kmedoids.inertia_:.2f}")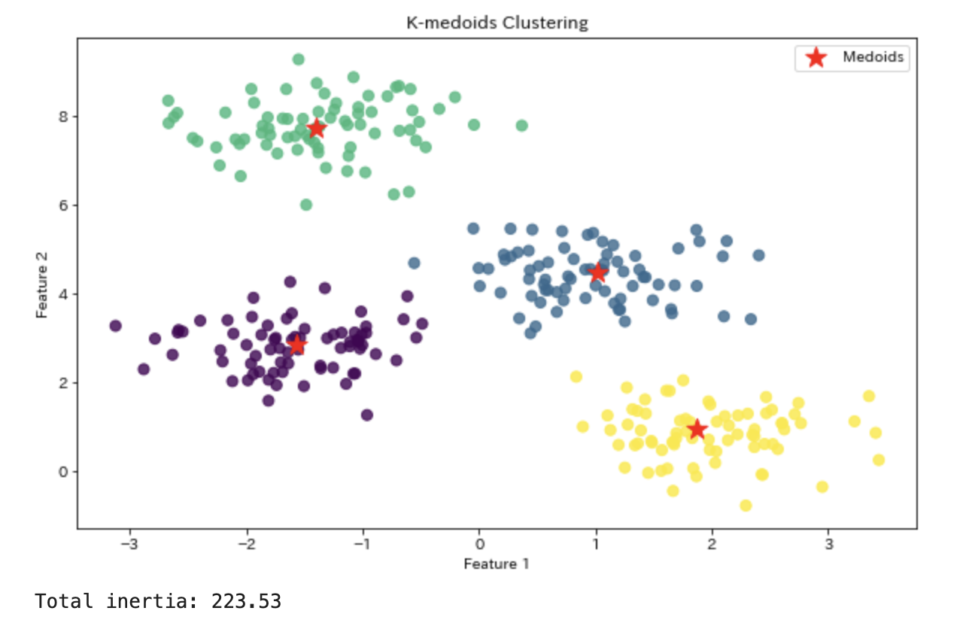
K-medoidsのメリットデメリット整理
メリット
- ロバスト性
- 外れ値に対して堅牢で、K-meansよりも信頼性の高い結果を提供することがある
- 距離メトリクスの柔軟性
- 任意の距離や非類似度メトリクスを使用可能
- 解釈可能性
- medoidは実際のデータポイントなので、解釈がしやすい
- カテゴリカルデータへの適用
- 数値データだけでなく、カテゴリカルデータにも適用可能
- 直感的な結果
- 各クラスターが実際のデータポイントによって表されるため、結果が直感的に理解しやすい
デメリット
- 計算コスト
- $O(n^2 \cdot k \cdot i)$の時間複雑性を持ち、大規模データセットでは非効率
- スケーラビリティ
- データサイズが大きくなると急速に計算時間が増加
- 初期medoid選択への依存
- 初期medoidの選択によって結果が変わることがある
- 局所最適解
- グローバルな最適解を保証しない
- クラスター数の事前指定
- K-meansと同様に、クラスター数$k$を事前に指定する必要がある
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!




