階層型クラスタリング徹底比較｜ウォード法・最短距離法などの使い分け
階層的クラスタリングとは？
クラスタリングは、教師なし学習の基本的な手法の一つであり、類似したデータ点をグループ化することで、ラベル付けされていないデータから有益な情報を抽出する手法です。
中でも階層的クラスタリングは、データ点間の類似度に基づいて段階的にクラスタを形成していく手法です。
この過程は樹形図（デンドログラム）として視覚的に表現されるため、結果の解釈が容易になります。
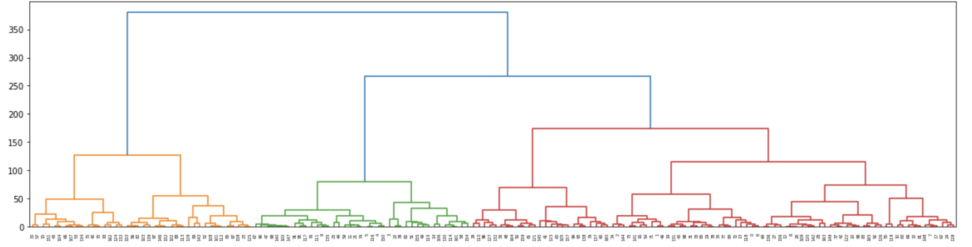
こんな感じですね。
一般的には、個々のデータ点をそれぞれ一つのクラスタとして出発し、最も類似性の高いクラスタ同士を繰り返し統合していくボトムアップ（凝集型）のアプローチが採用されます。
2. 階層的クラスタリングの7つの代表的手法
階層的クラスタリングの大きな特徴は、事前にクラスタの数を指定する必要がないことです。これにより、データの構造が未知の場合でも探索的に分析を進めることができます。K-means法などの分割クラスタリングとは異なり、階層的クラスタリングではデンドログラムを切断する高さを選ぶことで、後からでも異なるレベルのクラスタリング結果を検討できるため、データに対するより深い洞察を得ることが可能です。
階層的クラスタリングには、クラスタ間の距離（または類似度）をどのように定義するかによって、様々な手法が存在します。
ここでは、代表的な7つの手法について詳しく解説します。
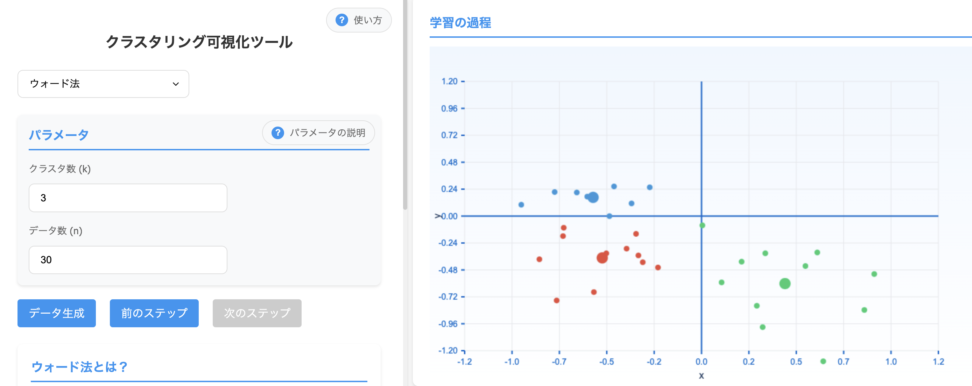
2.1 ウォード法（Ward’s Method）
ウォード法は、クラスタ内の分散の増加を最小限に抑えながらクラスタを統合していく手法です。
数学的背景
ウォード法は、クラスタを統合する際に情報損失を最小化するという考えに基づいています。情報損失は、二乗誤差和（SSE: Sum of Squared Errors）の増加量として定量化されます。
各クラスタのセントロイド（重心）は、そのクラスタに属するデータ点の平均ベクトルとして計算されます。
二つのクラスタ $C_i$ と $C_j$ を統合した際の分散増加量は次式で表されます
$${\Delta Var(C_i, C_j) = \frac{|C_i| \cdot |C_j|}{|C_i| + |C_j|} \cdot ||{\mu_i – \mu_j}||^2}$$
- $|C|$ はクラスタのサイズ（データ点の数）
- $\mu$ はセントロイドを表します。
アルゴリズム
- すべてのデータ点を個別のクラスタとして初期状態とします
- 各ステップで、可能なすべてのクラスタペアを統合した場合の、クラスタ内分散の増加量を計算します
- 分散の増加量が最も小さい二つのクラスタを統合し、新たな一つのクラスタを形成します
- このプロセスは、すべてのデータ点が単一のクラスタに統合されるか、あらかじめ設定されたクラスタ数に達するまで繰り返されます
メリットとデメリット
クラスタ形状と外れ値の影響
ウォード法は一般的にバランスの取れた、やや球形またはコンパクトなクラスタを生成する傾向があります。外れ値は分散を増加させるため、統合プロセスに影響を与え、最適でないクラスタ構造につながる可能性があります。
補足｜DIANA法
DIANA（Divisive Analysis）法は、階層的クラスタリングの一種で、分割型の手法です。
一般的な凝集型（agglomerative）の階層クラスタリング（例：ウォード法）とは逆のアプローチを取ります。
- すべてのデータを1つの大きなクラスターとする ところから開始。
- ウォード法は「ボトムアップ型」（小さなクラスタを統合）ですね。
- クラスタ内のデータ間の距離を考慮し、最も異質なデータ点の集合を特定。
- その集合を分割し、2つのクラスターに分ける。
- このプロセスを繰り返し、最適なクラスタリング結果が得られるまで進める。
ウォード法は分割時に分散が最小化されるように統合するのに対し、DIANA法は異質性の大きい部分を切り離すことでクラスターを形成します。正直あんまり使われないです。
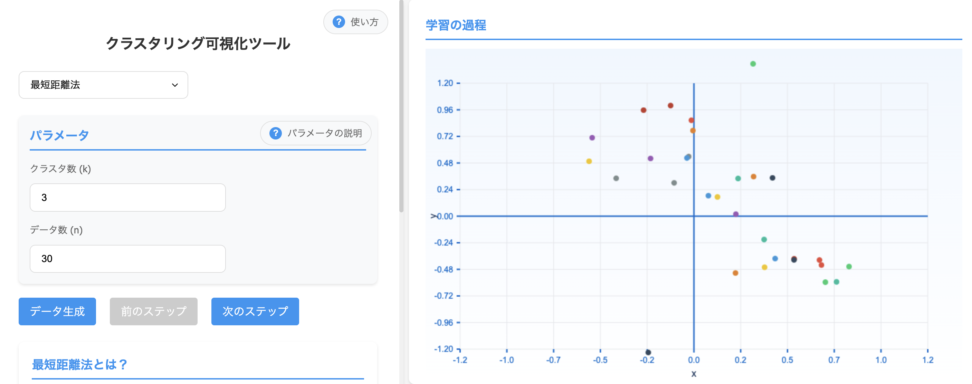
2.2 最短距離法（Single Linkage）
最短距離法は、二つのクラスタに属する任意の二点間の距離のうち、最も短い距離に基づいてクラスタを統合していく手法です。
数学的背景
二つのクラスタ $C_1$ と $C_2$ 間の距離は次式で定義されます
$${d(C_1, C_2) = \min_{x \in C_1, y \in C_2} d(x, y)}$$
- $d(x, y)$ は点 $x$ と点 $y$ の間の距離（多くの場合ユークリッド距離）
アルゴリズム
- 初期状態では、各データ点が個別のクラスタとして扱われます
- 各ステップで、すべてのクラスタペア間で最も距離の短い二点を見つけます
- これらの二点を含むクラスタを統合し、一つのクラスタを形成します
- このプロセスは、すべてのデータ点が単一のクラスタに統合されるまで繰り返されます
メリットとデメリット
クラスタ形状と外れ値の影響
最短距離法は細長く、鎖状の形状を形成する傾向があります。
外れ値はブリッジとして機能し、本来分離しているクラスタを早期にマージさせる可能性があるため、外れ値に対してロバストではありません。
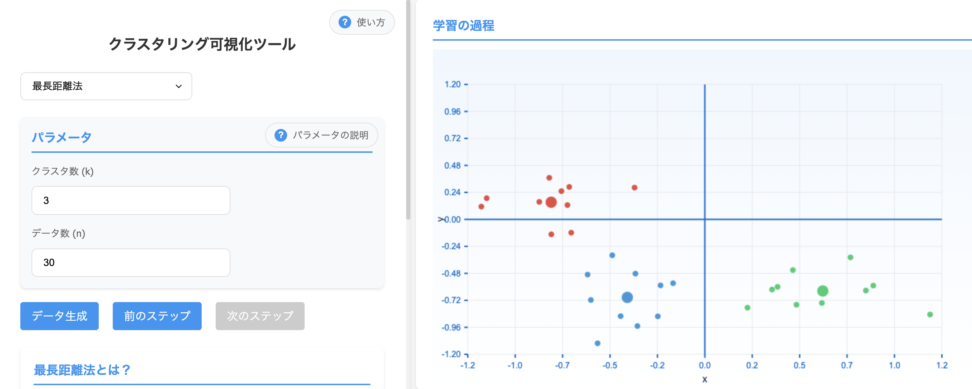
2.3 最長距離法（Complete Linkage）
最長距離法は、二つのクラスタに属する任意の二点間の距離のうち、最も長い距離に基づいてクラスタを統合する手法です。
数学的背景
二つのクラスタ $C_1$ と $C_2$ 間の距離は次式で定義されます：
$${d(C_1, C_2) = \max_{x \in C_1, y \in C_2} d(x, y)}$$
アルゴリズム
- 初期状態では、各データ点が個別のクラスタとして扱われます
- 各ステップで、異なるクラスタに属するすべての点のペアを考慮します
- そして、二つのクラスタ間で、最も遠い二点間の距離が最小となるペアを見つけます
- これらの二つのクラスタを統合します
このプロセスは、すべてのデータ点が単一のクラスタに統合されるまで繰り返されます
メリットとデメリット
クラスタ形状と外れ値の影響
最長距離法はコンパクトで、多くの場合やや球形または球状の形状を形成する傾向があります。
外れ値はクラスタ間の最大距離を増加させ、本来起こりうる統合を遅らせたり妨げたりする可能性があるため、外れ値に対して敏感です。
2.4 群平均法（Average Linkage）
群平均法は、統合する二つのクラスタに属するすべての点間の距離の平均に基づいて、クラスタを統合する手法です。
数学的背景
二つのクラスタ $C_1$ と $C_2$ 間の距離は次式で定義されます：
$${d(C_1, C_2) = \frac{1}{|C_1||C_2|} \sum_{x \in C_1} \sum_{y \in C_2} d(x, y)}$$
- $|C|$ はクラスタ $C$ 内の点の数
- $d(x, y)$ は点 $x$ と点 $y$ の間の距離です。
アルゴリズム
- 初期状態では、各データ点が個別のクラスタとして扱われます
- 各ステップで、すべてのクラスタペアについて、一方のクラスタの点と他方のクラスタの点のすべての可能なペア間の距離の平均を計算します
- そして、平均距離が最も小さい二つのクラスタを統合します
このプロセスは、すべてのデータ点が単一のクラスタに統合されるまで繰り返されます
メリットとデメリット
クラスタ形状と外れ値の影響
群平均法は最短距離法や最長距離法と比較して、よりバランスの取れた適切に形成されたクラスタを生成する傾向があります。
平均化により外れ値の影響は軽減されますが、完全に排除されるわけではありません。
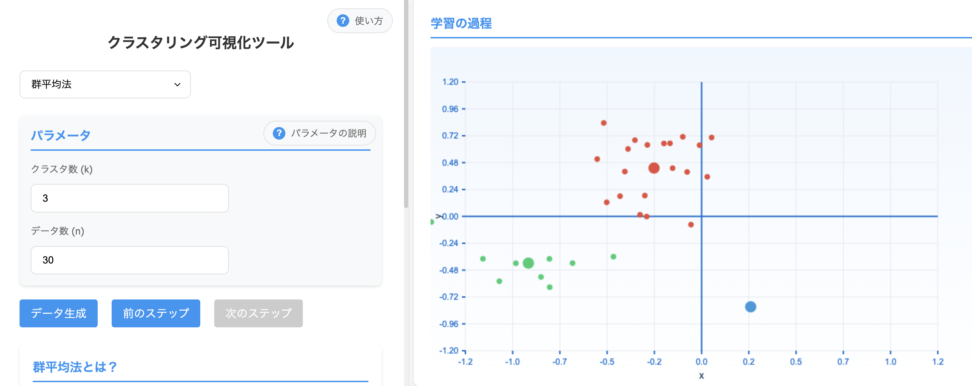
2.5 重心法（Centroid Method）
重心法は、各クラスタをそのセントロイド（平均ベクトル）で代表させ、二つのクラスタのセントロイド間の距離に基づいてマージを決定する手法です。
数学的背景
クラスタ $C = {x_1, x_2, …, x_n}$ のセントロイド $\mu$ は、その点の平均として計算されます
$${\mu = \frac{1}{n} \sum_{i=1}^{n} x_i}$$
二つのクラスタ間の距離は、それぞれのセントロイド間の距離（通常はユークリッド距離）となります。
アルゴリズム
- 初期状態では、各データ点が個別のクラスタとして扱われます
- 各ステップで、すべてのクラスタのセントロイドを計算します
- そして、セントロイド間の距離が最小となる二つのクラスタを見つけます
- これらの二つのクラスタをマージし、マージされたクラスタの新しいセントロイドを計算します。
このプロセスは、すべてのデータ点が単一のクラスタに統合されるまで繰り返されます。
二つのクラスタをマージした後、新しいクラスタのセントロイドは、マージされる前の二つのクラスタのセントロイドの加重平均として計算されます。
$${\mu_{new} = \frac{|C_1|\mu_1 + |C_2|\mu_2}{|C_1| + |C_2|} }$$
- ${|C_i| }$ はクラスタ ${C_i}$ のサイズ
- ${\mu_i }$ はそのセントロイド
メリットとデメリット
クラスタ形状と外れ値の影響
重心法は、比較的均一なサイズのクラスタを形成する傾向があります。外れ値はセントロイドの計算に影響を与えますが、群平均法と同様に、単一の外れ値がクラスタリング全体に大きな影響を与えることはありません。
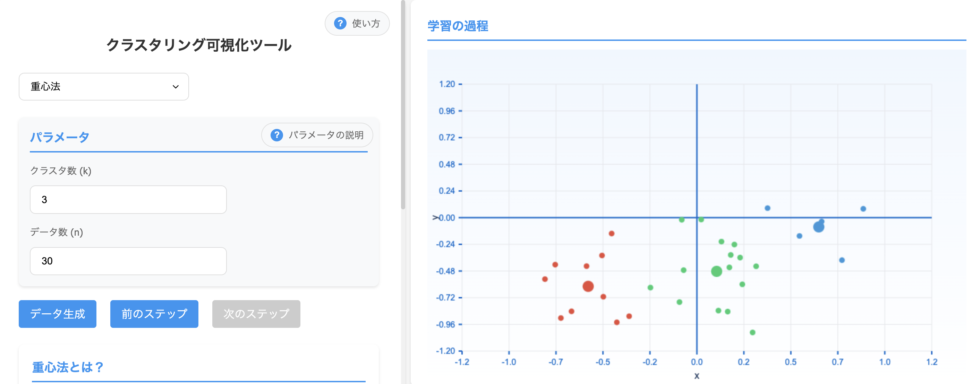
2.6 重み付き平均法（Weighted Average Linkage）
重み付き平均法は、群平均法の拡張版で、クラスタのサイズに基づいて距離計算に重みを付ける手法です。
数学的背景
二つのクラスタC_1 と C_2間の距離は次式で定義されます
$${d(x,y)d(C_1, C_2) = \frac{1}{w_1 w_2} \sum_{x \in C_1} \sum_{y \in C_2} w_x w_y d(x, y) }$$
- ${w_1}$と ${w_2}$ はそれぞれのクラスタの重み（多くの場合、クラスタサイズ）
- ${w_x}$ と ${w_y}$ は個々のデータ点の重み
アルゴリズム
- 初期状態では、各データ点が個別のクラスタとして扱われます
- 各ステップで、すべてのクラスタペアについて、重み付き平均距離を計算します
- 重み付き平均距離が最小となる二つのクラスタを統合します
- 新しいクラスタの重みは、統合された二つのクラスタの重みの和として計算されます
- このプロセスは、すべてのデータ点が単一のクラスタに統合されるまで繰り返されます
メリットとデメリット
クラスタ形状と外れ値の影響
重み付き平均法は、クラスタのサイズに基づいて距離計算に重みを付けるため、大きなクラスタと小さなクラスタの統合に対してより慎重になります。
これにより、クラスタサイズの偏りがある場合でも、より均衡のとれた結果が得られる傾向があります。外れ値の影響は、重みの設定によって軽減されますが、完全に排除されるわけではありません。
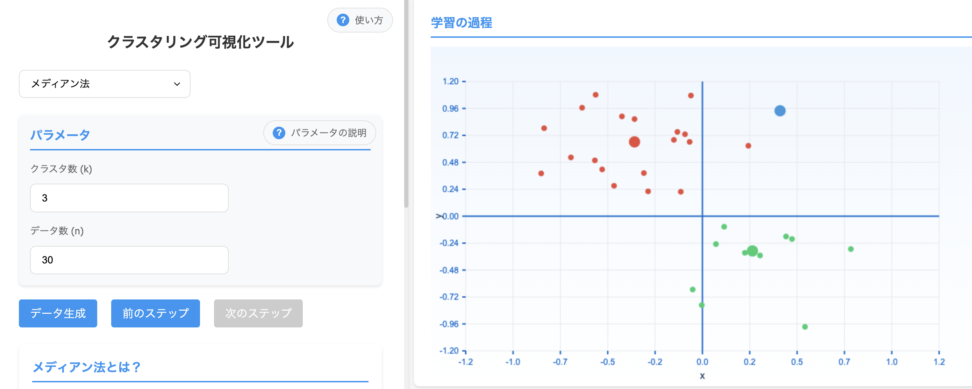
2.7 メディアン法（Median Method）
メディアン法は、重心法の一種で、クラスタサイズの影響を最小限に抑えるために、セントロイドではなくメディアン（中央値）を使用する手法です。
数学的背景
メディアン法では、二つのクラスタ C1C_1 C1 と C2C_2 C2 のメディアンを計算し、それらの間の距離に基づいてクラスタを統合します。クラスタのメディアンは、そのクラスタに属するデータ点の各次元の中央値として計算されます。
二つのクラスタをマージした後の新しいメディアンは、以下の式で計算されます
$${med_{new} = \frac{med_1 + med_2}{2}}$$
- ${med_i}$ はクラスタ ${C_i}$ のメディアン
重要なのは、クラスタのサイズに関係なく均等に重みづけされることです。
アルゴリズム
- 初期状態では、各データ点が個別のクラスタとして扱われます
- 各ステップで、すべてのクラスタのメディアンを計算します
- メディアン間の距離（通常はユークリッド距離）が最小となる二つのクラスタを見つけます
- これらの二つのクラスタを統合し、新しいクラスタのメディアンを計算します
- このプロセスは、すべてのデータ点が単一のクラスタに統合されるまで繰り返されます
メリットとデメリット
クラスタ形状と外れ値の影響
メディアン法は中央値を使用するため、極端な値の影響を受けにくく、より安定したクラスタリング結果になります。
外れ値が存在する場合でも、クラスタの代表点（メディアン）の計算に与える影響は限定的です。
まとめ！
階層的クラスタリングの7つの手法を理解したところで、それぞれの特徴と適用場面を比較しましょう。
3.1 手法の特性比較
| 手法名 | 連結基準 | 数学的基礎 |
| ウォード法 | クラスタ内分散の増加を最小化 | マージ時の二乗誤差和（SSE）を最小化 |
| 最短距離法 | 二つのクラスタの点間の最小距離 | クラスタ間で最も近い点のペアに基づいてマージ |
| 最長距離法 | 二つのクラスタの点間の最大距離 | クラスタ間で最も遠い点のペアに基づいてマージ |
| 群平均法 | クラスタ内のすべての点ペア間の平均距離 | 二つのクラスタのすべての点間の平均的な近さを考慮 |
| 重心法 | 二つのクラスタのセントロイド間の距離 | 平均ベクトルが最も近いクラスタをマージ |
| 重み付き平均法 | クラスタサイズによる加重平均距離 | マージされるクラスタのデータ点の数を考慮して平均距離を計算 |
| メディアン法 | マージされるクラスタのセントロイドの中央値 | 新しいセントロイドはセントロイドの中央値に関連付けられる |
3.2 選択基準
最適な階層的クラスタリング手法を選択する際は、以下の要素を考慮することが大事かなと思います。
- データの性質
- 高次元データ、外れ値の存在、データの分布など
- 予想されるクラスタ形状
- 球形、非球形、チェーン状など
- クラスタサイズの均一性
- 同じようなサイズのクラスタが必要か否か
- 計算リソース
- 大規模データセットの場合、計算効率が重要
- 解釈のしやすさ
- 結果の解釈と説明が必要な場合の考慮
3.3 使い分けどうしたらいい？
- ウォード法
- クラスタ内の均質性が重要な場合
- （例：顧客セグメンテーション）
- 最短距離法
- 非球形クラスタや連続的なパターンを検出する場合
- （例：地理的なパターン）
- 最長距離法
- 明確に分離されたクラスタが必要な場合
- （例：画像セグメンテーション）
- 群平均法
- 一般的な探索的分析や、バランスの取れた結果が必要な場合
- 重心法
- 多次元データで、クラスタの中心が重要な場合
- 重み付き平均法
- クラスタサイズの差が大きい場合
- メディアン法
- 外れ値が存在する可能性が高い場合
