超幾何分布をわかりやすく解説｜非復元抽出

1. 超幾何分布

1.1 超幾何分布とは

超幾何分布は、有限個からなる母集団から非復元抽出を行うときに、「特定の属性を持つ要素がサンプル中に何個含まれるか」を表す確率分布です。

例示：品質検査への応用

• ロット内に製品が ${N}$ 個あり、そのうち不良品が ${M}$ 個含まれている。
• 無作為に ${n}$ 個を検査する（非復元抽出）。
• 検査した中で不良品が ${k}$ 個含まれる確率を知りたい。

このとき、確率変数 ${X}$（「取り出したうち属性を持つ要素の数」）がちょうど ${k}$ となる確率は、次式の超幾何分布に従います。

$${\displaystyle P(X = k) = \frac{ \binom{M}{k} \binom{N – M}{\,n – k} }{ \binom{N}{n} }, \quad (k = 0, 1, \dots, n)}$$

${\binom{a}{b}}$ は ${a}$ 個の中から ${b}$ 個を選ぶ組合せの数を表します。

1.2 幾何分布や二項分布との違い

• 幾何分布や二項分布は、多くの場合「復元抽出」（＝試行の独立性が成り立つ）を前提としており、抽出するたびに母集団の状態は変化しません。
• 一方、超幾何分布では、一度取り出した要素を戻さないため、母集団の構成比率が試行のたびに変化します。

2. 数学的背景

2.1 基本公式

前述した超幾何分布の確率質量関数（PMF）は、改めて書くと

$${P(X = k) = \frac{ \binom{M}{k} \,\binom{N – M}{\,n – k} }{ \binom{N}{n} }}$$

• ${N}$: 母集団の大きさ
• ${M}$: 母集団のうち特定属性を持つ要素の数
• ${n}$: 抜き取るサンプル数
• ${k}$: サンプル中で特定属性を持つ要素の数

というパラメータを持ちます。

2.2 期待値と分散

期待値

$${E[X] = n \times \frac{M}{N}}$$

直感的にも、サンプル ${n}$ のうち ${\frac{M}{N}}$​ の割合で属性を持つ要素が含まれる、という解釈です。

分散

$${\mathrm{Var}(X) = n \times \frac{M}{N} \times \left(1 – \frac{M}{N}\right) \times \frac{N – n}{N – 1}}$$

二項分布との差分となる係数 ${\frac{N – n}{N – 1}}$が、非復元抽出ゆえの「母集団が減っていく」効果を示しています。

2.3 ベイズ推定との組み合わせ

超幾何分布は、ベイズ推定フレームワークの中で尤度関数として用いられることがあります。

たとえば、

$${\displaystyle P(N \mid \text{data}) \;=\; \frac{ P(\text{data} \mid N)\,\, P(N) }{ P(\text{data})}, \quad \text{where}\;\; P(\text{data} \mid N) \;\sim\; \text{Hypergeometric}(N, M, n)}$$

のように、観測データに対して超幾何分布を当てはめることで、母集団や属性要素の真の数（あるいはサンプルにおける分布）を更新して推定するのです。

論文での応用例｜双子移植システム（マウスモデル）

さて、ここまでで一通りの超幾何分布の説明はできたと思うので、実際どのような研究に使われているのかをガッツリ深掘ります。

なかなか免疫学に触れていないと、小難しいとは思います。

ただ、サイコロやおみくじ等の具体例だけだと、テストの問題が解けるだけだと思うので、統計学を実務や研究に落とし込むためにもこういった実例にも少しずつ触れていただければと思います。

3.1 研究背景

Microbiota dictate T cell clonal selection to augment graft-versus-host disease after stem cell transplantation

上の論文では、マウスの同一ドナーから採取した T 細胞プールを、遺伝的に同一な2匹（双子）のレシピエントに移植して飼育する、という「Twin Transplant System」を用いています。

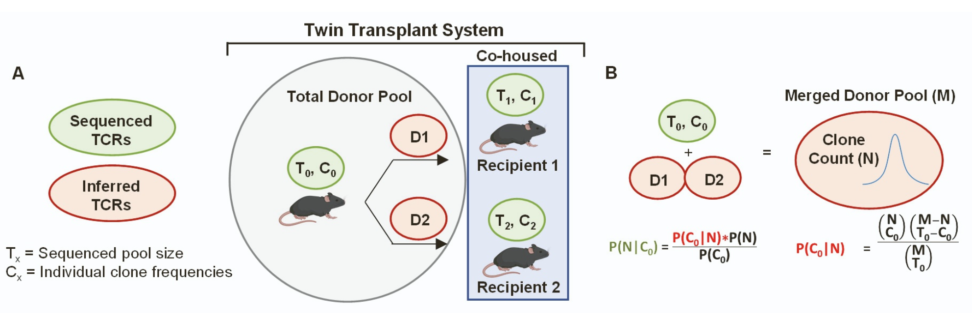
図のとおり「D1, D2」とラベルされた推定されたドナー TCRが各レシピエントに移るため、どちらのレシピエントにも共通して移行したクローンもあれば、一方にしか存在しないクローンもあります（非復元的な分配）。

3.2 なぜ超幾何分布が登場するか？

• 有限母集団：ドナー TCR の総数（あるいは解析可能なプール）
• 非復元抽出：それを 2匹（あるいは複数）のレシピエントに分割移植する
• 分割後のクローン観測数：各レシピエントでシーケンスした際に確認できるクローン数

上述のように、あるクローンを「どれくらいの確率でレシピエントAに移ったか？ レシピエントBに移ったか？」というのは、ちょうど超幾何分布で説明できる構造を持ちます。

とりわけ「Aでも観測され、Bでも観測される確率」や「Aには観測されるが B には観測されない確率」などを尤度として使う場合に、非復元抽出を前提とする超幾何分布が自然に適合します。

3.3 具体的な分析の流れ

当該論文では、

1. ドナープール中の TCR（${T_0, C_0}$​）
2. レシピエント1, 2 それぞれで観測された TCR（${T_1, C_1,T_2, C_2}$​）
3. ドナー→レシピエントへの移行過程を「超幾何分布 + ベイズ」的にモデル化

することにより、「実際にはシーケンスされなかったクローンを含めて、どれくらいのクローンがどのように振り分けられたか」を確率的に推定します。

3.3.1 ベイズの定理を使ったモデリング

論文では、ベイズの定理で表した尤度の部分を超幾何分布で表しています。

$${P(C_0 \mid N) = \frac{ \binom{N}{c_0} \,\binom{M – N}{\,T_0 – c_0} }{ \binom{M}{T_0} }}$$

ここで ${\binom{N}{c_0}}$は「母集団 ${N}$ のうち ${c_0}$​ をどう取り出すか」、${\binom{M – N}{T_0 – c_0}}$ は「残りから残りの数をどう補うか」……という非復元的な組合せが並んでいます。

これによって、移植後にどのクローンが顕著に増えているのか（グラフト拒絶や免疫反応に関与しているのか）を定量的に評価できるわけです。

実際に移植片対宿主病（GvHD）の発症や重症度に大きく影響するクローンを特定できることは、臨床上の治療戦略（例：T細胞の選別や免疫抑制剤のデザイン）の検討に重要です。

3.3.2 尤度関数を超幾何分布で記述

$${\begin{aligned} P(N \mid C_0) &= \frac{P(C_0 \mid N) \, P(N)}{P(C_0)}, \\ P(C_0 \mid N) &\sim \text{Hypergeometric} \quad (\text{超幾何分布}), \end{aligned}}$$

上式の意味を噛み砕くと、

1. 事前に「TCRクローンの大きさ ${N}$」に対する仮定（これを ${P(N)}$ としてモデリング）
2. 実際に観測されたクローン頻度（${C_0}$​）が得られる確率を超幾何分布で評価（これを ${P(C_0 \mid N)}$）
3. 観測データ${C_0}$​ を踏まえて、クローンサイズ ${N}$ がどの程度あり得るか（これが ${P(N \mid C_0)}$）

という流れでベイズ的に推定するわけです。

4. ビジネス・アカデミア実務での有用性

今回は、免疫系のトピックを紹介しましたが、ビジネスにどう応用できるかも考えてみました。

実は限られた資源（母集団）を複数のサンプルに分配するという場面一般に応用できると考えていて、たとえばビジネスのデータ分析でも

• マーケティングの複数キャンペーンに割り当てた顧客リストの配分
• 商品在庫のロット分割と検品サンプル
• 金融商品ポートフォリオのサブセット選定

など、「有限集団をサブセットに分配して“抜き取り検査”する」状況では、二項分布のような“復元抽出”前提のモデルではなく、超幾何分布を使ったほうが実態を正確に反映できるのではと考えています。

今日は以上！！