自己組織化マップとは？データの視覚的探索と次元削減の手法

自己組織化マップとは？

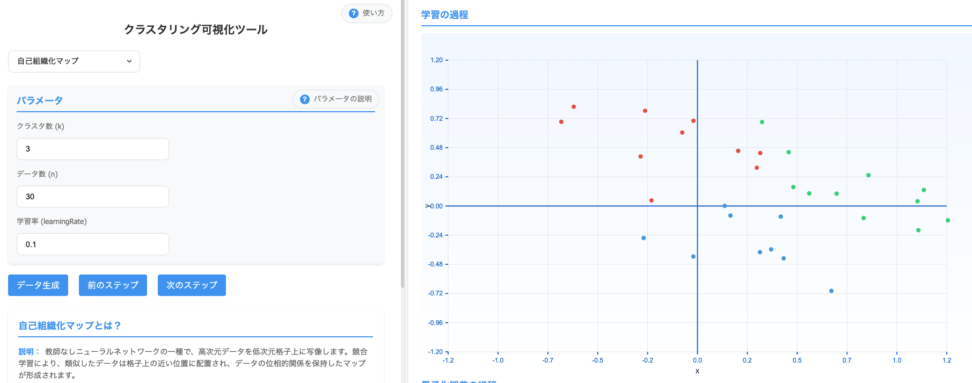
自己組織化マップ（Self-Organizing Map,SOM）は、高次元のデータを2次元（時には1次元や3次元も）の格子状に配置されたニューロンの集合体に投影することで、データの可視化と理解を容易にするクラスタリング手法です。

こちらのシミュレーションツールも合わせて学習いただくと理解しやすいと思います。

クラスタリング可視化ツール｜自己組織化マップ

トポロジー保存性？

最大の特徴は、「トポロジー保存性」という性質です。

これは、元の高次元空間で互いに近いデータが、SOM上でも近い位置に配置されるという特性を指します。つまり、SOMはデータの類似性を維持しながらマッピングを行い、視覚的にデータの構造を把握できるようにします。

他の次元削減手法との違い

• 主成分分析（PCA）
  • 線形変換を用いて、データの分散を最大にする方向（主成分）にデータを投影します。数学的にはデータの共分散行列の固有値分解に基づいています。
• t-SNE
  • 局所的な類似性を保存することに焦点を当て、特に非線形なデータ構造の可視化に優れています。
• SOM
  • 競合学習とニューロンの協調的適応を通じて、入力データの分布の形状を反映する離散的なマップを作成します。

自己組織化マップの数学的背景

アーキテクチャ

SOMは一般に2次元の格子状に配置されたニューロン（またはノード）の集合で構成されます。各ニューロン $i$ は、入力データと同じ次元を持つ重みベクトル $w_i$ を持っています。例えば、3次元の入力データを扱う場合、各ニューロンも3次元の重みベクトルを持ちます。

SOMの格子は通常、正方形または六角形の配列として設計されます。

学習プロセスの直感的理解

2次元空間に分布するデータ点があるとします。初期状態では、SOMの格子は規則的に配置されていますが、学習が進むにつれて格子は歪み、データの分布に適応していきます。

• 初期状態
  • 格子は規則的で、データの分布とは無関係です。
• 学習の初期段階
  • 格子全体がデータの分布に向かって大きく変形します。これは近傍半径が大きく、広範囲のニューロンが更新されるため。

• 学習の中期段階
  • 格子はデータの全体的な構造に適応し始め、クラスタの大まかな形状が現れます。
• 学習の後期段階
  • 近傍半径が小さくなり、ニューロンは局所的に微調整され、データの細かい構造を捉えます。

データが密集している領域では格子も密になり、データが少ない領域では格子は疎になります。

学習アルゴリズム

SOMの学習アルゴリズムは、次の主要なステップで構成されています

1. 初期化
   • すべてのニューロンの重みベクトルをランダムに初期化します。
2. 競合
   • 各入力データ点に対して、最も類似したニューロン（勝者ニューロン）を見つけます。
3. 協力
   • 勝者ニューロンの近傍にあるニューロンも、その入力に対して更新されます。
4. 適応
   • 勝者ニューロンとその近傍のニューロンの重みが、入力データに近づくように更新されます。

これらのステップは多数の入力サンプルに対して何度も繰り返され、マップが徐々に入力データの分布を表現するように自己組織化していきます。

勝者ニューロンの選択

入力ベクトル $x$ に対して、勝者ニューロン $c$ は次のように選ばれます

$${c = \arg\min_i |x – w_i|}$$

• $|x – w_i|$
  • 入力ベクトル $x$ とニューロン $i$ の重みベクトル $w_i$ とのユークリッド距離

重み更新ルール

SOMの学習プロセスの核心は重み更新ルールです。

時刻 $t$ における更新式は次のように表されます

$${w_i(t+1) = w_i(t) + \alpha(t) \cdot h_{ci}(t) \cdot [x(t) – w_i(t)]}$$

• $\alpha(t)$ は学習率で、時間とともに減少する値
  • 例：$\alpha(t) = \alpha_0 \cdot \exp(-t/\tau_1)$
• $h_{ci}(t)$ は近傍関数で、勝者ニューロン $c$ からニューロン $i$ までの距離に基づいて決まります。

近傍関数としてよく使われるのはガウス関数です

$${h_{ci}(t) = \exp\left(-\frac{|r_c – r_i|^2}{2\sigma(t)^2}\right)}$$

• $r_c$ と $r_i$ はそれぞれ勝者ニューロン $c$ とニューロン $i$ の格子上の位置ベクトルです。
• $\sigma(t)$ は近傍半径で、時間とともに減少します
  • 例：$\sigma(t) = \sigma_0 \cdot \exp(-t/\tau_2)$

自己組織化マップの実装例

Pythonを使用してSOMを実装し、実際のデータに適用する例を見てみましょう。

minisomというライブラリを使用します。

import numpy as np
import matplotlib.pyplot as plt
from minisom import MiniSom
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler

# アヤメデータセットの読み込み
iris = load_iris()
X = iris.data
y = iris.target

# データの正規化（0-1の範囲に）
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)

# SOMの定義（5x5の格子、入力ベクトルは4次元）
som_grid_size = 5
som = MiniSom(som_grid_size, som_grid_size, X.shape[1], sigma=1.0, learning_rate=0.5, 
              neighborhood_function='gaussian')

# ランダム初期化
som.random_weights_init(X_scaled)

# 学習（1000回のイテレーション）
som.train(X_scaled, 1000)

# 勝者ニューロンの計算
winner_coordinates = np.array([som.winner(x) for x in X_scaled])
cluster_index = np.ravel_multi_index(winner_coordinates.T, (som_grid_size, som_grid_size))

# 結果の可視化
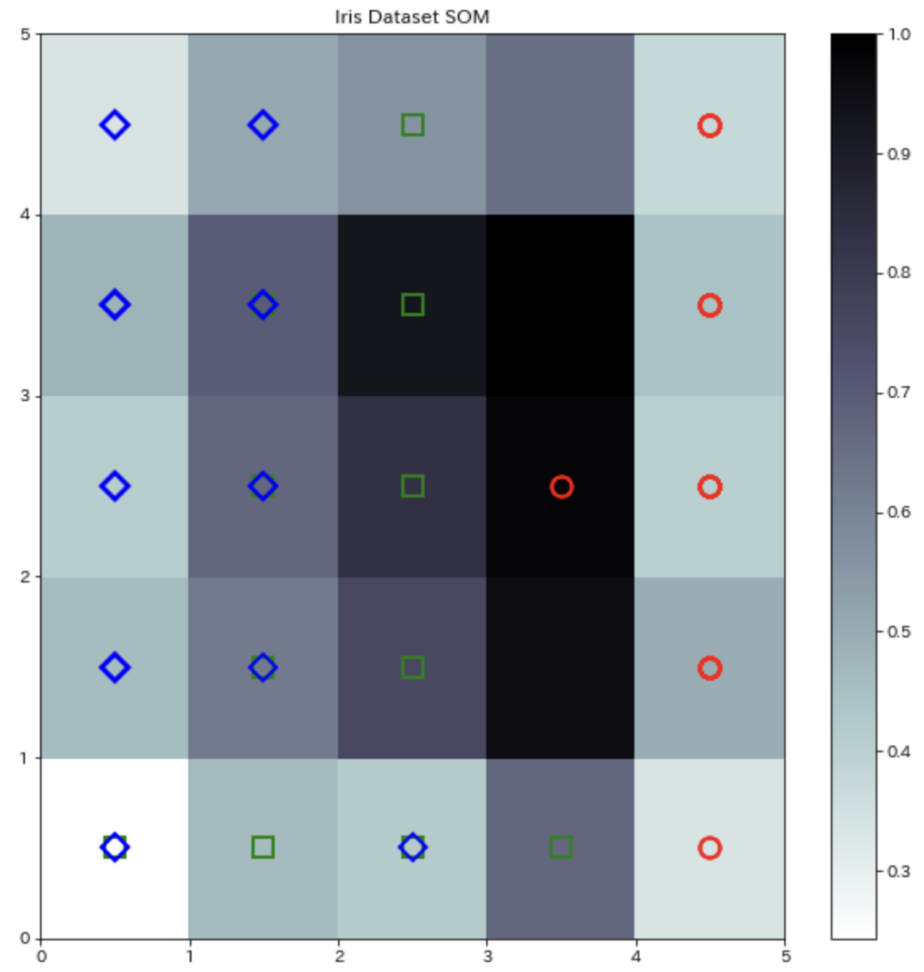
plt.figure(figsize=(10, 10))
plt.pcolor(som.distance_map().T, cmap='bone_r')  # U-matrixの可視化
plt.colorbar()

# クラス毎に異なるマーカーでプロット
colors = ['red', 'green', 'blue']
markers = ['o', 's', 'D']
for i, (x, t, c) in enumerate(zip(X_scaled, y, cluster_index)):
    plt.plot(winner_coordinates[i][0] + 0.5, winner_coordinates[i][1] + 0.5, 
             markers[t], markerfacecolor='None', 
             markeredgecolor=colors[t], markersize=12, markeredgewidth=2)

plt.title('Iris Dataset SOM')
plt.show()

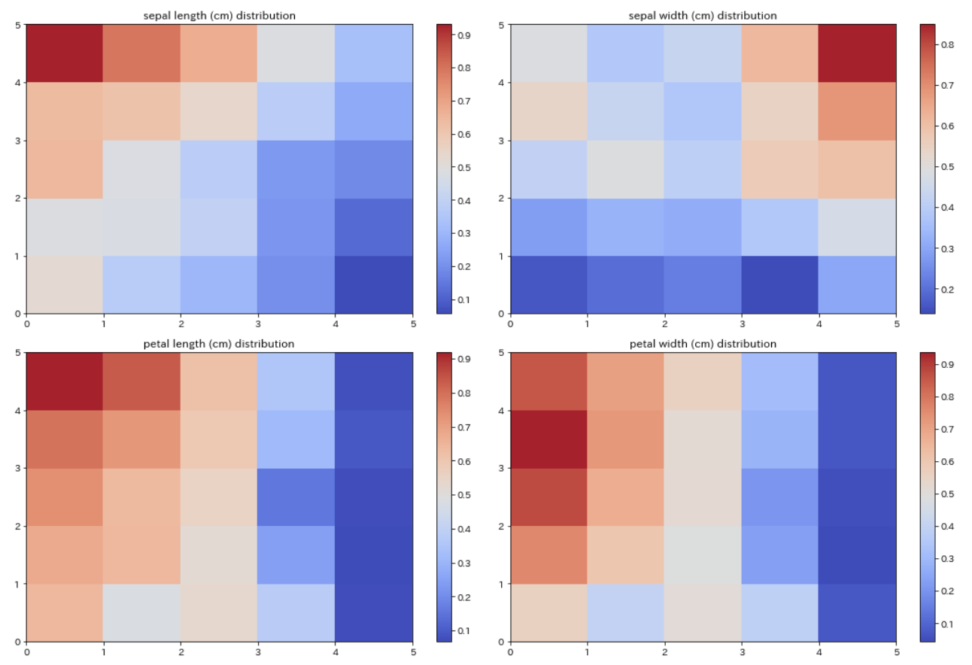
# 特徴量の分布の可視化
feature_names = iris.feature_names
plt.figure(figsize=(15, 10))
for i, name in enumerate(feature_names):
    plt.subplot(2, 2, i+1)
    plt.pcolor(som.weights[:,:,i].T, cmap='coolwarm')
    plt.colorbar()
    plt.title(f'{name} distribution')

plt.tight_layout()
plt.show()

結果の解釈

上記のコードを実行すると、次のような可視化結果が得られます

• U-matrix
  • 各ニューロンとその隣接ニューロン間の距離を示します。明るい領域はニューロン間の距離が大きく、クラスタの境界を表し、暗い領域はニューロン間の距離が小さく、同じクラスタに属するデータを表します。

• 特徴量の分布
  • 各特徴量のヒートマップは、その特徴量の値が高い領域（暖色）と低い領域（寒色）を示します。これにより、各特徴量がクラスタ形成にどのように寄与しているかを理解できます。

評価指標

定量化誤差（Quantization Error, QE）

定量化誤差は、各データポイントとその勝者ニューロンの距離の平均です

$${QE = \frac{1}{n} \sum_{j=1}^{n} |x_j – w_{c(j)}|}$$

• $n$ はデータポイントの数
• $c(j)$ はデータポイント $j$ の勝者ニューロン

トポロジカル誤差（Topological Error, TE）

トポロジカル誤差は、データポイントの最も近いニューロンと2番目に近いニューロンが格子上で隣接していない割合を測定します。

低いTEは、トポロジーがよく保存されていることを示します(冒頭で言ったトポロジー保存の話です。)

$${TE = \frac{1}{n} \sum_{j=1}^{n} u(x_j)}$$

• $u(x_j)$
  • データポイント $j$ の最も近いニューロンと2番目に近いニューロンが隣接していない場合は1
  • そうでない場合は0

×

FOLLOW ME ！

@blue_statistics