母平均の区間推定と検定 – 正規分布と標準誤差の概念

こんにちは、青の統計学です！

今回は、母平均の区間推定と検定 について解説します

統計検定2級で頻出の分野ですので、分散が未知、既知の場合も含めてぜひ押さえて欲しいです。

動画で学びたい方はこちらをどうぞ。

【統計的推定】聞き流して学ぶデータサイエンス｜母平均、母分散、母比率の推定までわかりやすく解説

はじめに

私たちが本当に知りたいのは、目の前にある標本（サンプル）の平均値ではありません。当然ですが、知りたいのは、その標本が属する母集団の真の平均値、すなわち母平均 $\mu$です。

例えば、あるECサイトの全ユーザーの平均購入額を知りたいとしましょう。全ユーザー（母集団）を調査するのは時間的にもコスト的にも非現実的です。そこで、ランダムに選んだ1,000人のユーザー（標本）の平均購入額を計算します。これが標本平均 $\bar{X}$です。

標本平均 $\bar{X}$ は、母平均 $\mu$ の点推定値として有用です。しかし、標本はあくまで母集団の一部を切り取ったものに過ぎません。別の1,000人を選べば、標本平均はわずかに異なる値になるでしょう。

数学的背景：標本平均の分布について

区間推定や検定といった推測統計学の議論は、すべて標本平均 $\bar{X}$ がどのような確率分布に従うかという土台の上に成り立っています。

中心極限定理について

母集団の平均を $\mu$、分散を $\sigma^2$ とします。母集団からサイズ $n$ の標本を無作為に抽出するとき、標本平均 $\bar{X}$ はそれ自体が確率変数となります。

この標本平均 $\bar{X}$ の分布に関して、便利な定理があります。

それが中心極限定理 (Central Limit Theorem, CLT)です。

この定理の「母集団の分布がどのような形であっても」という点が嬉しいポイントです。

これにより、母集団の分布を知らなくても、標本サイズさえ大きければ、正規分布という扱いやすい分布を使って推測を行うことができるのです。

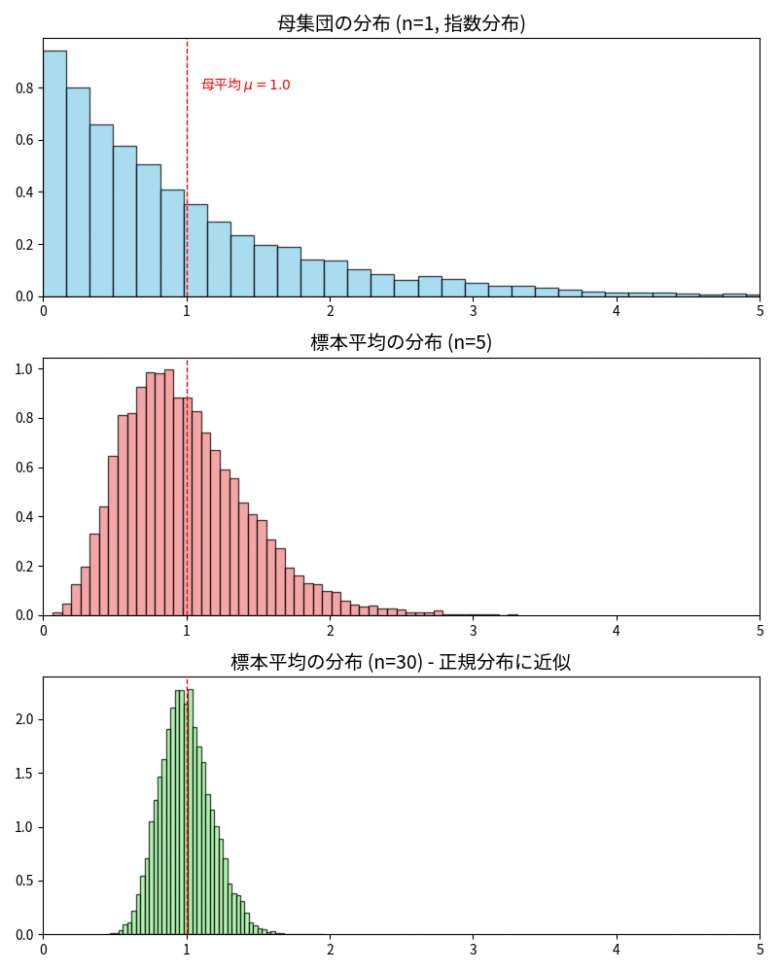
上の図をご覧いただくと、中心極限定理のイメージがつくと思います。

標本サイズ $n$ の増加に伴う標本平均の分布の変化。母集団が指数分布であっても、$n$ が大きくなるにつれて標本平均の分布は正規分布に近づいている様子がわかります。

【中心極限定理】聞き流して学ぶデータサイエンス

標準誤差について

標本平均 $\bar{X}$ の分布の標準偏差 $\sqrt{\sigma^2/n}$、すなわち $\sigma/\sqrt{n}$ は、標準誤差 (Standard Error, SE) と呼ばれます。

$${ \text{SE} = \frac{\sigma}{\sqrt{n}} }$$

標準誤差は、標本平均 $\bar{X}$ が母平均 $\mu$ からどれくらいばらつくか、つまり推測の精度を表す指標ですね。

• $\sigma$（母標準偏差）
  • 母集団自体のばらつきが大きいほど、標本平均もばらつきやすくなります。
• $\sqrt{n}$（標本サイズの平方根）
  • 標本サイズ $n$ が大きくなるほど、標準誤差は小さくなります。これは、より多くのデータを集めるほど、標本平均が母平均に近づき、推測の精度が上がることを数学的に示しています

区間推定の本質：Z分布とt分布の使い分け

区間推定の目的は、標本平均 $\bar{X}$ を中心として、母平均 $\mu$ が存在するであろう「幅」を計算することです。この幅は、次の一般的な構造で計算されます。

$${ \text{信頼区間} = \bar{X} \pm (\text{信頼係数に対応する値}) \times \text{標準誤差} }$$

ここで、「信頼係数に対応する値」を決めるために、Z分布とt分布という2つの分布を使い分けます。この使い分けこそが、区間推定の本質的な理解に繋がります。

母分散 $\sigma^2$ が「既知」の場合：Z分布の利用

もし、母集団の分散 $\sigma^2$（したがって標準偏差 $\sigma$）が既知であれば、標準誤差 $\text{SE} = \sigma/\sqrt{n}$ は真の値として確定します。

このとき、標本平均 $\bar{X}$ を標準化した検定統計量 $Z$ は、厳密に標準正規分布 $N(0, 1)$ に従います。

$${ Z = \frac{\bar{X} – \mu}{\sigma/\sqrt{n}} \sim N(0, 1) }$$

信頼係数 $1-\alpha$ に対応する信頼区間は、標準正規分布の上側 $\alpha/2$ 点 $z_{\alpha/2}$ を用いて次のように計算されます。

$${ \bar{X} \pm z_{\alpha/2} \frac{\sigma}{\sqrt{n}} }$$

母分散 $\sigma^2$ が「未知」の場合：t分布の登場

現実のデータ分析では、母平均 $\mu$ が未知であるのと同様に、母分散 $\sigma^2$ も未知であることがほとんどです。ばらつきがわかってるなら、もはや母平均も分かりそうですね。

母分散 $\sigma^2$ が未知の場合、標本から計算した不偏分散 $s^2$を使って、標準誤差を推定するしかありません。この推定された標準誤差を $\hat{\text{SE}}$ とします。

$${ \hat{\text{SE}} = \frac{s}{\sqrt{n}} }$$

ここで、検定統計量 $T$ を考えると、分母の $\sigma$ が推定値 $s$ に置き換わったことで、新たな不確実性が加わります。

$${ T = \frac{\bar{X} – \mu}{s/\sqrt{n}} }$$

この $T$ は、標準正規分布には従いません。

代わりに、自由度 $n-1$ の $t$ 分布に従います。

なぜ $t$ 分布が必要なのか？

$t$ 分布は、標準正規分布と比べて裾野が重い（厚い）という特徴があります。

これは、極端な値（外れ値）が出やすいことを意味します。

それは、分母の標準誤差 $\hat{\text{SE}}$ が標本によって変動する推定値だからです。

• 標本平均 $\bar{X}$ の変動
  • 標本平均 $\bar{X}$ は、母平均 $\mu$ の周りでばらつきます（これはZ分布でも考慮済み）。
• 標準誤差 $\hat{\text{SE}}$ の変動
  • さらに、標準誤差の推定値 $\hat{\text{SE}}$ も、標本ごとに変動します。

$T$ 統計量は、この2つの推定による不確実性を同時に内包しています。特に標本サイズ $n$ が小さいとき、不偏分散 $s^2$ の推定精度は低く、$\hat{\text{SE}}$ が真の標準誤差 $\text{SE}$ から大きくズレる可能性があります。

$t$ 分布の重い裾野は、この標準誤差の推定に伴う不確実性を数学的に補正するために存在します。

確率分布可視化ツール｜t分布

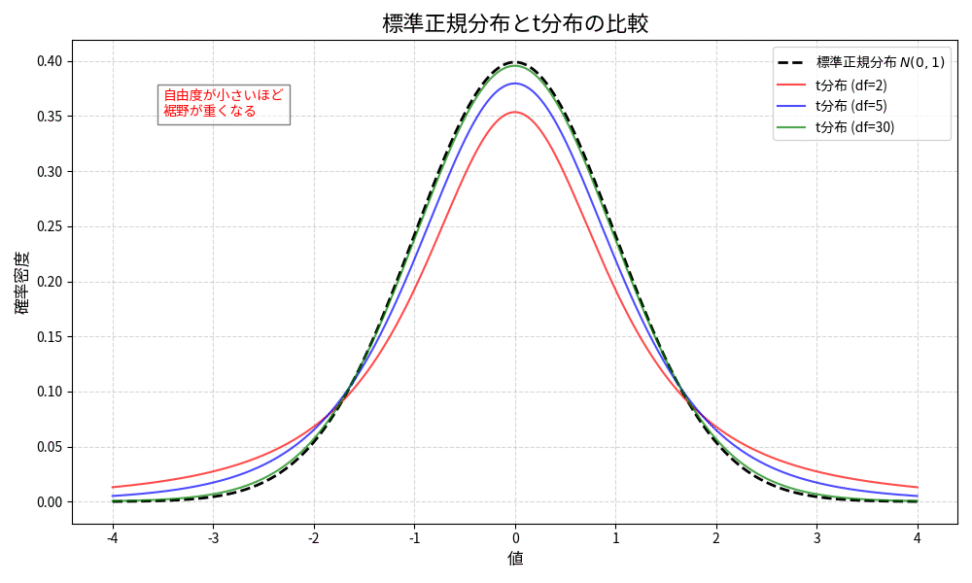
図：標準正規分布と自由度の異なる $t$ 分布の比較。自由度が小さいほど裾野が重く、自由度が大きくなるにつれて標準正規分布に収束する。

$t$ 分布は、自由度 $n-1$ が大きくなる（つまり標本サイズ $n$ が大きくなる）につれて、標準正規分布に収束していきます。

信頼係数 $1-\alpha$ に対応する信頼区間は、自由度 $n-1$ の $t$ 分布の上側 $\alpha/2$ 点 $t_{\alpha/2, n-1}$ を用いて次のように計算されます。

$${ \bar{X} \pm t_{\alpha/2, n-1} \frac{s}{\sqrt{n}} }$$

検定統計量と信頼区間の関係

仮説検定では、まず帰無仮説 $H_0$（例えば「母平均 $\mu$ はある特定の値 $\mu_0$ である」）を設定します。そして、標本データがこの $H_0$ の下でどれだけ起こりにくいかを評価します。

評価に使うのが、区間推定で登場した統計量と同じ構造を持つ検定統計量です。

条件	検定統計量	従う分布
母分散 $\sigma^2$ 既知	$Z = \frac{\bar{X} – \mu_0}{\sigma/\sqrt{n}}$	標準正規分布 $N(0, 1)$
母分散 $\sigma^2$ 未知	$T = \frac{\bar{X} – \mu_0}{s/\sqrt{n}}$	$t$ 分布（自由度 $n-1$）

$\mu_0$ は帰無仮説で設定した母平均の値です。

もし、計算された検定統計量の値が、有意水準 $\alpha$ で定められた棄却域に入れば、それは「$H_0$ の下では、この標本平均 $\bar{X}$ は珍しい」ことを意味し、$H_0$ を棄却します。

$p$ 値：起こりにくさの定量化

とはいえ、検定統計量が棄却域に入るかどうかを判断する代わりに、$p$ 値を使う方法が一般的です。

$p$ 値とは、「帰無仮説 $H_0$ が正しいと仮定したとき、今回得られた標本データ、あるいはそれ以上に極端なデータが得られる確率」のことです。

• $p$ 値が小さい（例: $p < 0.05$）
  • $\implies$ $H_0$ の下では起こりにくい $\implies$ $H_0$ を棄却し、対立仮説 $H_1$ を採択する。
• * $p$ 値が大きい（例: $p \ge 0.05$）
  • $\implies$ $H_0$ の下でも十分に起こり得る$\implies$ $H_0$ を棄却できない。

$p$ 値は、検定統計量の値が、その分布（$Z$ 分布または $t$ 分布）のどの位置にあるかを定量的に示している、つまり検定統計量の値と分布の面積を繋ぐ役割を果たしています。

備考｜2標本の比較への繋がり

母平均の推測は、さらに発展的なテーマである2標本の比較へと繋がります。

2つの母集団の平均 $\mu_1$ と $\mu_2$ の差 $\mu_1 – \mu_2$ について検定を行う場合も、基本的な構造は変わりません。

1. 帰無仮説: $H_0: \mu_1 = \mu_2$（差がない）

2. 検定統計量: $\frac{(\bar{X}_1 – \bar{X}_2) – (\mu_1 – \mu_2)}{\text{標準誤差}}$

このとき、2つの標本の分散が等しいと仮定できるか（等分散性）どうかで、標準誤差の計算方法と、検定統計量が従う $t$ 分布の自由度が変わってきます。特に、分散が等しいと仮定できない場合に用いられるのがウェルチの $t$ 検定というのものがあります。

詳しくは、こちらの記事をご覧ください。