対数正規分布とは？ビジネスで使える便利な確率分布

1. 対数正規分布とは？

まず、抑えて欲しいのが

対数正規分布は、「ある変数 ${X}$ の対数 ${\ln(X)}$が正規分布に従う」ときに、変数${X}$そのものが従う分布のことです。
より具体的には、確率変数${X}$に対して

$${\ln(X) \sim N(\mu, \sigma^2)}$$

が成り立つとき、${X}$は対数正規分布に従うといいます。
ここで、

• ${\ln(\cdot)}$ は自然対数（log base e）
• ${N(\mu, \sigma^2)}$は平均 ${\mu}$、分散 ${\sigma^2}$の正規分布

を表します。

正規分布については、こちらの記事をご覧ください

1.1. 直感的イメージ

多くのビジネスデータ（例：売上、顧客単価、閲覧数など）では、その値が0に近いものから非常に大きな値まで広範囲にわたることがよくあります。

こうした片側（多くは0より大きい側）に偏ったデータは、対数変換を施すと正規分布に近づく傾向があります。

2. 対数正規分布の確率密度関数

対数正規分布に従う確率変数${X}$の確率密度関数は、次の式で表せます。

$${f_X(x) = \frac{1}{x \sigma \sqrt{2 \pi}} \exp\left(-\frac{(\ln x – \mu)^2}{2\sigma^2}\right), \quad x > 0}$$

ここで

• ${\mu}$は${\ln(X)}$の平均（location parameter）
• ${\sigma}$は ${\ln(X)}$の標準偏差（scale parameter）

を意味します。
要点として、${x}$は常に正の値を取るという特徴があります。

これはビジネスで扱うデータが多くの場合、マイナスにならない（売上・価格など）という現象をうまく捉えています。

3. 対数正規分布の特徴・正規分布との違い

ここでは、正規分布と比較した対数正規分布の特徴を見てみます。

まずは可視化してみましょう。

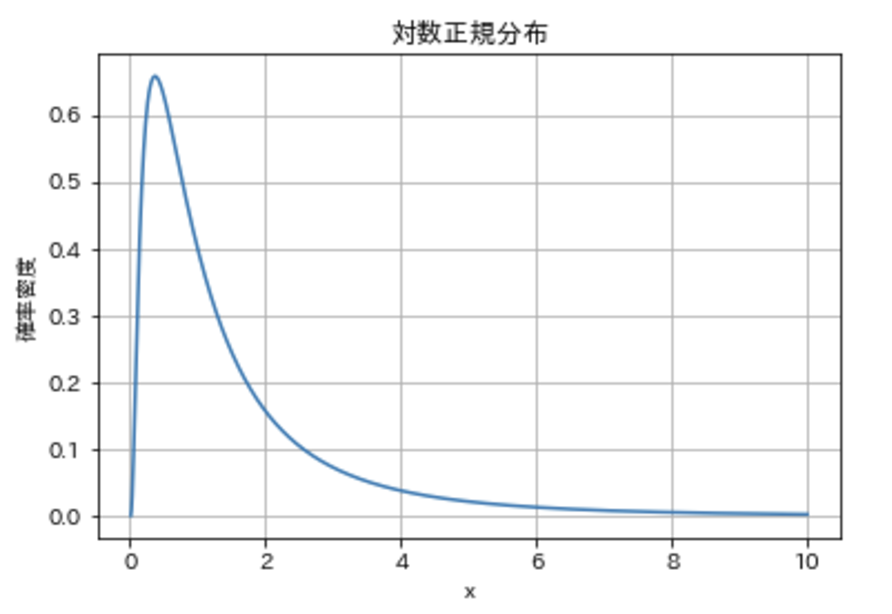
右に裾を引く特徴的な形状ですね。

3.1 非対称性

正規分布は左右対称ですが、上図の通りで対数正規分布は右裾が長い（右への裾が肥大）形状を持ちます。

これはビジネスデータにおいて、少数の大きな値（ハイエンド顧客や一部の巨大売上） が存在し、母集団全体の分布を歪ませる現象を表現できます。

3.2 平均・中央値・最頻値の違い

正規分布では平均＝中央値＝最頻値ですが、対数正規分布では3つが一致しません。

特にビジネスでは、「値のばらつきが大きく、極端な外れ値が全体の平均を引き上げる」ようなデータがしばしばあるため、平均だけ見ると誤解を生む可能性があります。

年収の分布とかがそうですね。

このとき、

• 中央値が「典型的な値」を示す
• 平均値は「一部の大きい値の影響を受けやすい」

といった点を区別して分析を行う必要があります。

あとの具体例でちょっと触れます。

3.3 乗算的効果を表現する

対数正規分布が自然に登場する大きな理由として、「乗算的効果」が繰り返される現象をモデル化できるという点があります。ビジネスにおける売上やコストは、複数の要因が掛け合わさって増減します。

乗算の結果が対数空間での加算に相当し、それによって ${\ln(X)}$が正規分布に近づくため、対数正規分布が頻出するわけです。

4. ビジネスでの活用例：在庫管理・需要予測

4.1 在庫管理における対数正規分布の有用性

企業が在庫管理を行う際、需要の変動は大きなリスクになります。需要が正規分布ではなく、歪んだ形をとっているケースは多く、伝統的な正規分布を前提としたモデルを用いると「極端に大きな需要が起こり得るリスク」を過小評価しやすいです。
対数正規分布を仮定することで、需要のばらつきが大きく、右裾が長い分布をうまく捕捉できるようになります。そのため、

• 過剰在庫リスク（需要が思ったほど伸びず在庫を抱える）
• 機会損失リスク（需要が急増した際に品切れを起こす）

の両面を合理的に評価できるのです。

4.2 シナリオ設定

ある小売企業が、ある商品Aの月間需要を予測したいとします。

過去12か月の販売実績から、月次需要${X}$の対数（${\ln(X)}$）をプロットしてみると正規分布に近い形状が得られたため、「${X}$は対数正規分布に従う」と仮定しました。

• ${\ln(X)}$の平均: ${\mu = 3.0}$
• ${\ln(X)}$ の標準偏差: ${\sigma = 0.7}$

ここで、${X}$の分布は対数正規分布 ${\mathrm{Lognormal}(3.0, 0.7^2)}$となります。

4.3 代表値の計算

対数正規分布の代表値を確認しましょう。

1. 平均
   • ${E[X] = \exp\left(\mu + \frac{\sigma^2}{2}\right) = \exp(3.0 + \frac{0.7^2}{2}) = \exp(3.0 + 0.245) = \exp(3.245) \approx 25.70}$
   • つまり、月間需要の平均値は約25.7個と見積もられます。
2. 中央値
   • ${\mathrm{Median}(X) = \exp(\mu) = \exp(3.0) \approx 20.09}$
   • 平均よりも中央値が小さいことがわかります。少数の大きな需要が平均を押し上げている典型的な対数正規分布の特徴です。
3. 最頻値（モード）
   • ${\mathrm{Mode}(X) = \exp(\mu – \sigma^2) = \exp(3.0 – 0.7^2) = \exp(3.0 – 0.49) = \exp(2.51) \approx 12.30}$
   • 最も頻繁に出現しやすい需要は約12.3個となります。

4.4 需要に応じた在庫戦略の策定

分析して、意思決定に影響を与えるまでがデータサイエンスなので、ここから何が解釈できて、どういう意思決定プロセスを改善できるのかを考えてみましょう。

さて、以下のように数値例からわかるように、平均値と最頻値が異なる場合、どの指標をベースに在庫を積むかによってリスクが変わります。

• 平均値(約26個)を採用して在庫を持つ
  需要が多い月は十分にカバーできるが、最も起こりやすいケース(約12個)に比べると在庫が過剰になる可能性が高い。
• 最頻値(約12個)を基準にすると
  在庫コストは抑えられるが、需要が多い月が来た場合に品切れを起こすリスクが高い。

どちらを優先するかは、ビジネス上のコスト構造（在庫保管コスト、品切れによる販売機会損失）によって異なります。

このように、対数正規分布を用いることで、単純な平均値による判断だけではなく、歪度が大きい現実の需要のリスクを考慮した在庫戦略を立案できるようになります。

個人的な意見ですが、IT領域だとにおいてウェブアクセス数やSNS拡散度合いなど、従来よりも裾が長い分布がビジネスの意思決定に影響を与えるケースはますます増加しています。

対数正規分布を活用することで、これらのデータ特性をある程度精緻に捉えることができると思います。