HPD区間をわかりやすく解説|信頼区間との違いは?
HPD(Highest Posterior Density Interval)区間とは
HPD区間は、指定された確率(例えば95%)を含む最小の区間を求めます。
事後分布から得られる区間であり、その区間に含まれる事後確率が最大となるような区間を指します。

確率密度が最も高い領域を、指定された確率(例えば95%)を満たすように切り出した区間のことです。
数学的な表現をすると、以下のようになります。
$${\int_{\text{HPD}}p(\theta|x)\,d\theta\geq\int_{\text{HPD}^c}p(\theta|x)\,d\theta}$$
ここで、$p(\theta|x)$は事後分布、$\theta$は母数、$x$はデータを表しています。
HPD区間内の確率密度を積分した値が、区間外の確率密度を積分した値以上である、つまり、HPD区間内に確率密度が集中しているということですね。
この区間はパラメータの点推定値よりも信頼性が高く、同時に複数のパラメータの推定も可能になるため、ベイズ統計における区間推定の指標としてよく使われています。
HPD区間の具体例
例えば、正規分布でHPD区間を可視化させてみました。
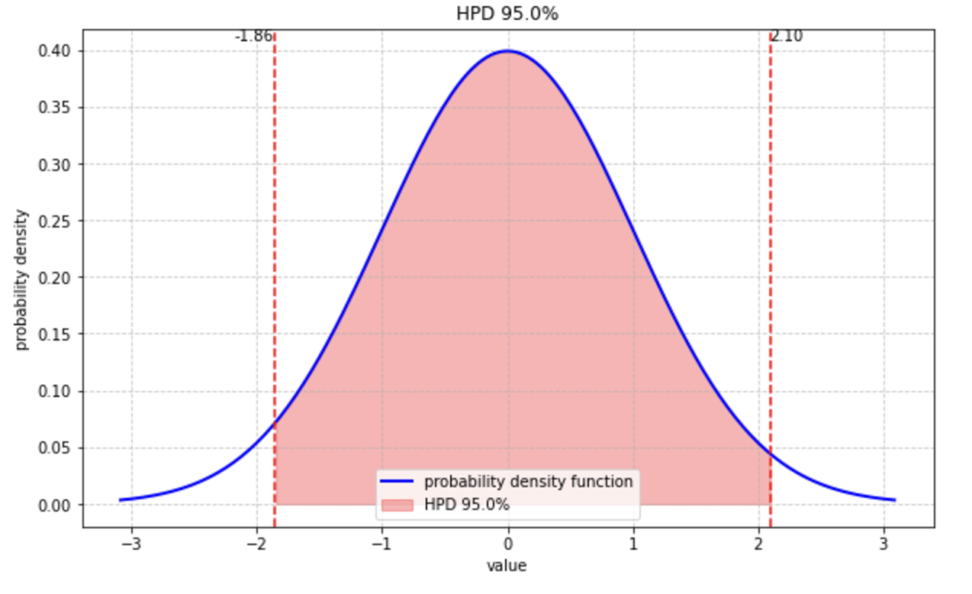
こちらはガンマ分布(形状パラメータ2、尺度パラメータ2)でのHPD区間です。
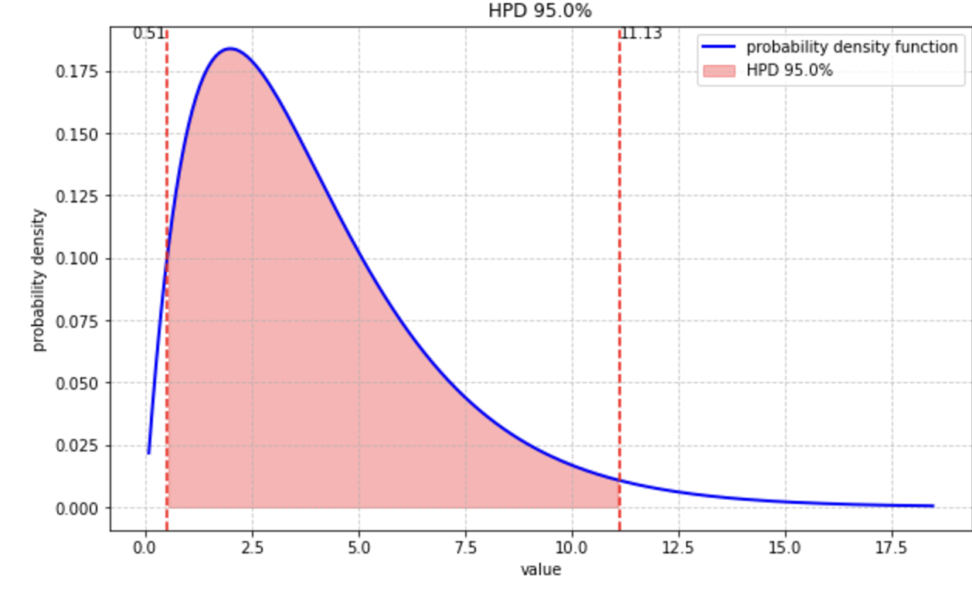
HPD区間の性質として、単峰性の事後分布においては、HPD区間は唯一つの連続した区間になります。
\(\alpha\)を所望の信頼水準(通常95%が使われます)とすると、HPD区間は$\int_{\text{HPD}}p(\theta|x)\,d\theta=1-\alpha$を満たす最小の区間となります。
HPD区間の性質
- 単峰性: 事後分布が単峰性(一つの山を持つ)の場合、HPD区間は唯一つの連続した区間になります。
- 多峰性: 事後分布が多峰性(複数の山を持つ)の場合、HPD区間は複数の区間に分かれる可能性があります。
とくに多峰性事後分布の場合、HPD区間は複数の区間になる可能性があります。
例えば、混合正規分布のような場合、複数のモード(最頻値)が存在するため、それぞれに対応するHPD区間が得られることがあります。
HPD区間の計算方法
区間の計算には、主に解析的な方法と数値的な方法の二つのアプローチがあります。
解析的な方法は、事後分布が既知の確率分布に従う場合に適用できます。
例えば、事後分布が正規分布に従う場合、その平均と分散から直接HPD区間を求めることができます。
正規分布の場合、HPD区間は平均を中心とする対称な区間となり、その幅は分散に基づいて決定されます。
図を再掲します。

具体的には、標準正規分布の分位点を用いて以下のように計算されます
$${[\mu – z_{\alpha/2}\sigma, \mu + z_{\alpha/2}\sigma]}$$
$\mu$は事後分布の平均、$\sigma$は標準偏差、$z_{\alpha/2}$は標準正規分布の上側$\alpha/2$分位点です。

しかし、多くの実際の問題では、事後分布が単純な形状を持たない場合があります。
そのような場合、数値的な方法が有効です。
数値的方法の中でも、マルコフ連鎖モンテカルロ法(MCMC)は特に広く用いられています。
これは、複雑な事後分布からサンプルを生成する手法であり、具体的な仕組みについては以下のコンテンツがオススメです。
MCMC法を使ったHPD区間の計算
ここでは、簡単な手順をご説明します。
MCMCを用いたHPD区間の計算手順はこんな感じです。
- 事後分布からのサンプリング: MCMC法を用いて、事後分布から多数のサンプルを生成します。
- サンプルのソート: 生成されたサンプルを、小さい順にソートします。
- HPD区間の探索: ソートされたサンプルから、指定された確率(例えば95%)を満たす最小の区間を探索します。具体的には、連続するサンプルの中で、その区間内のサンプル数が全体の95%になるような最小の区間を見つけます。
この数値的アプローチの嬉しさは、事後分布の形状に関わらず適用できることです。
MCMC法によって事後分布からサンプルを得た後、それらのサンプル値を降順に並べ、上位$(1-\alpha)$の割合に相当する範囲を求めることで、HPD区間を近似的に計算できます。
例えば、ベータ分布$\mathrm{Beta}(2,5)$を事前分布、観測データ$\boldsymbol{x}=(0.3,0.6,0.7)$とする状況を考えましょう。
この場合の事後分布は、ベイズの定理より$\mathrm{Beta}(2+\sum x_i, 5+3-\sum x_i)=\mathrm{Beta}(4.6,6.4)$となります。
ここからMCMCによりサンプルを$10^6$個生成し、それらを並べた値の上位95%の範囲を計算すると、95%HPD区間は$[0.3126, 0.8602]$となります。
つまり、母数の真値(真のパラメータ)がこの区間に入る確率は95%以上であると解釈できます

逆に、信頼区間では「母数の真値がこの区間に入る確率は95%以上」などの解釈はできません。ちょっとややこしいですが、信頼区間の「95%」という確率は、信頼区間を求める手順に付随するものであり、個々の区間が真のパラメータを含む確率そのものではありません。
補足|信頼区間とHPD区間の違い
先ほども少し補足しましたが、信頼区間とHPD区間は異なります。
詳しく見ていきましょう。
信頼区間
頻度論的アプローチでは、パラメータは固定された未知の値であると考えます。
信頼区間は、この固定されたパラメータを含む区間を、データのサンプリングを繰り返した場合の長期的な頻度で定義します。
信頼区間
パラメータは固定: 確率は、ある実験においては固定された値。確率的に変動するものではありません。
区間は変動: 信頼区間は、サンプルによって変わるため、固定された値ではない。
信頼区間を、的を射るゲームに例えてみましょう。
- 的: コインの真の表が出る確率
- 矢: 信頼区間
何度も矢を射ると、矢の95%が的の中心に近い範囲に当たる(信頼区間内に真のパラメータが含まれる)ことを期待できますが、1回の試行で矢が的に当たる確率を正確に95%と断言することはできませんね。
例えば、95%信頼区間は以下のように解釈されます
「もし同じ実験を何度も繰り返し、毎回95%信頼区間を計算するなら、その区間が真のパラメータ値を含む割合は長期的に95%になる」
母集団平均$\mu$の95%信頼区間は次のように表されます
$${[\bar{x} – 1.96 \cdot \frac{\sigma}{\sqrt{n}}, \bar{x} + 1.96 \cdot \frac{\sigma}{\sqrt{n}}]}$$
$\bar{x}$はサンプル平均、$\sigma$は母集団の標準偏差、$n$はサンプルサイズですね。

正規分布の場合、HPD区間は信頼区間と一致することが一般的です。当たり前ですが、正規分布の対称性と、確率密度関数の形が両端で急激に減少するという点から、確率密度が最も高い領域は、必然的に中央付近の対称な区間となるからです。
一方、HPD区間は、事後確率に基づいた区間であり、パラメータがその区間内に存在する確率を直接的に表しているという点で信頼区間とは異なります。
信頼区間の95%〜というのは、手続き的な確率であり、個々の区間がパラメータを含む確率を直接表すものではないですね。
HPD区間
パラメータは変動: パラメータは、ある確率分布に従って値を取るという見方をします
区間は変動: 事後分布は、データと事前分布から得られるものであり、データが変われば事後分布も変わるため、HPD区間も変化します
数学的には、95% HPD区間$[a, b]$は次の条件を満たします
$${P(a \leq \theta \leq b | x) = 0.95}$$ $${p(\theta_1|x) \geq p(\theta_2|x) \text{ for all } \theta_1 \in [a,b] \text{ and } \theta_2 \notin [a,b]}$$
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!




