パス解析をわかりやすく解説：因果推論からMMMまで
パス解析とは？
パス解析は、複数の変数間の因果関係を明らかにするための統計的手法です。
特に、構造方程式モデリング（SEM）の一種であり、観測変数のみを用いて因果関係を推定することができます。
潜在変数（観測できないもの）をモデルに取り込むのが、SEMの特徴ですね。
これにより、単なる相関分析では得られない深い洞察を得ることが可能です。
パス図の作成
まず、パス解析では因果関係の仮説を図式化し、パス図を作成します。
パス図の特徴1｜因果関係の可視化
- 変数間の関係を矢印で表現
- ノード（変数）とエッジ（因果関係）で構成されるグラフィカルモデル
- 直接効果と間接効果の同時分析が可能
ここで、変数はノードとして、因果関係は矢印で示されます。
矢印の向きは因果の方向を、太さは効果の強さを表現します。
次に、観測データを用いて各パスの係数を推定し、モデル全体の適合度を評価します。
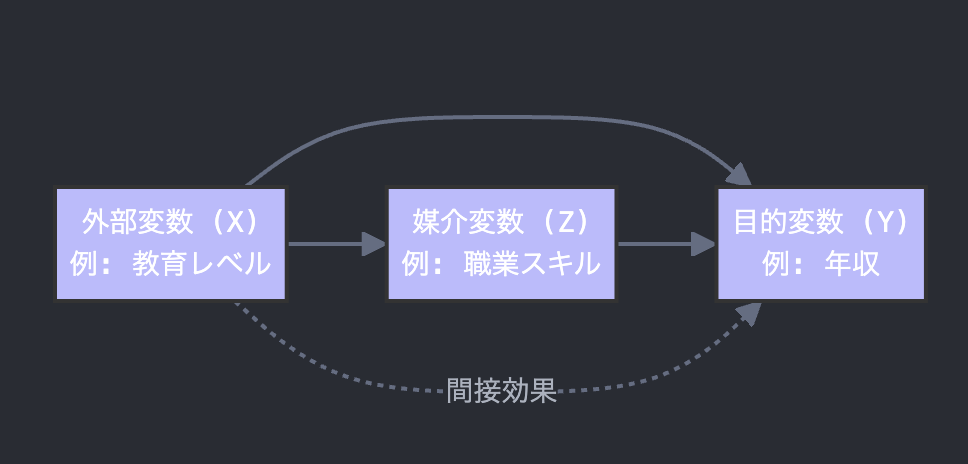
例えば、こんな感じです。
- 外部変数 (X): 例えば、「教育レベル」が
- 媒介変数 (Z): 「職業スキル」に直接影響を与え
- 目的変数 (Y): 「年収」に、直接および間接的に影響を与えるモデルです
矢印の意味
- 実線の矢印：直接効果
- 点線の矢印：間接効果
さらに、パス解析では${R^2}$を用いて各変数の説明力を評価し、間接効果を計算することで媒介変数の影響を明らかにすることも可能です。
パス解析を数式で理解する
パス解析は、変数間の因果関係を数式でモデル化することができます。
例えば、変数${X}$から${Y}$への直接的な影響を${\gamma_{XY}}$と表すと、次のようにモデル化されます
$${{Y = \gamma_{XY}X + \epsilon_Y}}$$
ここで、${\epsilon_Y}$は誤差項ですね。
さらに、${Z}$という変数が${Y}$に影響を与える場合、次のように複数の変数間の関係を表現できます
$${Y = \gamma_{XY}X + \gamma_{ZY}Z + \epsilon_Y}$$
$${Z = \gamma_{XZ}X + \epsilon_Z}$$
このように、パス解析では直接効果と間接効果を同時に推定し、因果関係を明らかにします。
パス図の特徴2|数学的背景
- 線形回帰の拡張として理解できる
- 標準化された係数（パス係数）を使用
- 誤差項を明示的に扱う
パス係数の推定と検定
パス係数は、一般的に最小二乗法を用いて推定されます。
推定されたパス係数の有意性を検定することで、変数間の因果関係の強さを評価します。
これにより、因果関係が統計的に有意であるかどうかを判断することができます。
具体的にみて見ましょう。
最小二乗法（Ordinary Least Squares, OLS）による推定
パス係数 ${\gamma}$ の推定は、残差平方和を最小化することで行われます。
線形回帰モデルの一般形を考えましょう
$${Y = \gamma_1X_1 + \gamma_2X_2 + … + \gamma_kX_k + \epsilon}$$
推定の目的は、${\gamma}$ ベクトルを最適化することです。
最小二乗法の目的関数
$${\min_{\gamma} \sum_{i=1}^{n} (Y_i – \sum_{k=1}^{K} \gamma_k X_{ik})^2}$$
さて、最小二乗推定量は、次の行列形式で表現できます
$$\hat{\gamma} = (X^T X)^{-1} X^T Y$$
- ${\hat{\gamma}}$ は推定されたパス係数ベクトル
- ${X}$ は説明変数の行列
- ${Y}$ は目的変数のベクトル
t検定による係数の有意性検定
では各パス係数 ${\gamma_k}$ の有意性を検定するために、t統計量を計算します。
- 帰無仮説：${H_0: \gamma_k = 0}$
- 対立仮説：${H_1: \gamma_k \neq 0}$
上のような仮説を設定します。
$${t = \frac{\hat{\gamma}_k}{SE(\hat{\gamma}_k)}}$$
- ${\hat{\gamma}_k}$ は推定されたパス係数
- ${SE(\hat{\gamma}_k)}$ は係数の標準誤差
ちなみに標準誤差は、分散共分散行列から得られます
$${SE(\hat{\gamma}k) = \sqrt{(X^T X)^{-1}{kk} \hat{\sigma}^2}}$$
有意水準の判定
一般的に、有意水準 ${\alpha = 0.05}$ を用いて判定します
- ${|t| > t_{critical}$ なら、係数は統計的に有意
- $p < \alpha$ なら、帰無仮説を棄却
パス解析を利用することで得られる利点は以下の通りです
まとめ｜パス解析の利点
- 複雑な因果関係の可視化：変数間の因果関係を図式的に表現し、分かりやすく可視化できます。
- 直接効果と間接効果の分離：各パスの寄与を明らかにします。
- 媒介変数の検出：ある変数が他の2つの変数間の関係を媒介するかどうかを検証できます。
- 交絡変数の制御：モデルに制御変数を含めることで、交絡変数の影響を制御します。
マーケティングミックスモデリング（MMM）への応用
実は、パス解析や構造方程式モデリングはマーケティングミックスモデリング（MMM）というモデルに利用されることがあります。
この辺のポストでも語っている通り、事業会社のマーケ部署等では集客費用を最適化する。
つまり、ROIが低いチャネルや施策からROIが高いチャネルや施策へ集客費用をアロケーションしようというのが、このモデルの前提にある思想です。
例えば、広告支出がブランド認知度を高め、その結果として購買意図が促進され、最終的に売上高に繋がるといったモデルを構築できます。この分析により、どのマーケティング施策に資源を集中すべきか、戦略の改善点を導き出すことができます。
さらに、SEMを用いることで潜在変数（例：ブランドロイヤルティ）を含んだより複雑なモデルを構築することが可能です。
これにより、より精緻な因果関係分析が行えます。
パス解析を使ったMMMはXICA社のMMMが特徴としていますね。
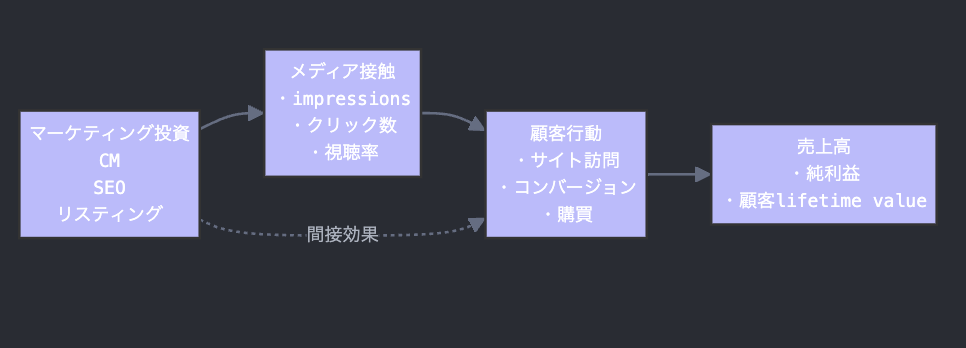
事業側のドメイン知識をもとに、チャネル間の論理関係を事前にインプットとしてパスを描き、モデリングするイメージですね。
この辺は業務でも取り組んでいる部分なので、深く扱っていこうと思います。
