トービットモデルとは？わかりやすく解説【潜在変数】｜計量経済学

トービットモデル

トービットモデルは、経済学や計量経済学で広く使用される回帰モデルの一種です。

このモデルは、従属変数が一定の値（通常は0）で切断されている状況を扱うためにつくられました。

モデルの基本構造と切断

トービットモデルは、潜在変数 $y^*$ を用いて以下のように定式化されます

$$y^* = \beta’x + \varepsilon$$

• $\beta$ はパラメータベクトル
• $x$ は説明変数ベクトル
• $\varepsilon$ は誤差項で、通常 $\varepsilon \sim N(0, \sigma^2)$ と仮定されます

潜在変数といっても訳わかんないですよね。

実際に観測される変数 $y$ は以下のように定義されます

$$y = \begin{cases} y^* & \text{if } y^* > 0 \\ 0 & \text{if } y^* \leq 0 \end{cases}$$

切断とは

上の式は何を意味しているのでしょうか？

簡単に言うと、「潜在的な意欲や傾向（$y^*$）が一定のレベルを超えたときだけ、実際の行動（$y$）として現れる」ということです。

例えば、「贅沢品への支出」を考えてみましょう。

人々は心の中で「こんなものが欲しい」という気持ち（$y^*$）を持っています。しかし、その気持ちが十分強くなるまで（$y^* > 0$）、実際には何も買わない（$y = 0$）ですよね。気持ちが十分強くなったときに初めて、実際の支出（$y > 0$）が発生するわけです。

この「見えない部分」と「見える部分」の関係を理解し、モデル化するのが、トービットモデルの大きな特徴です。潜在変数を考えることで、私たちは「なぜ人々がある行動を取るのか」「どんな要因が決定に影響しているのか」といった深い問いに迫ることができます。

可視化

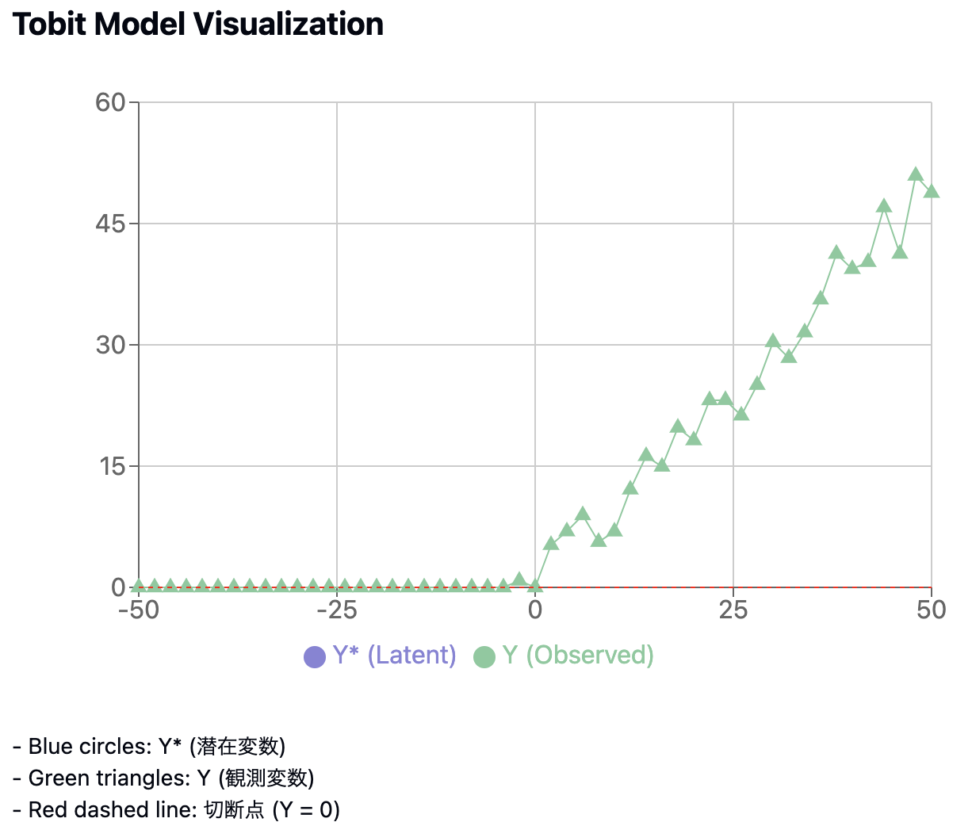
モデルを可視化してみましょう。

潜在変数 (\(Y*\))： 青い円で表されています。直接観察できない「真の」値を表しています。

観測変数 (\(Y\))： 緑の三角形で表されています。実際に観察される値です。

切断点： 赤い点線で示されています。この場合、\(Y = 0\) が切断点となっています。

潜在変数と観測変数の関係

• 切断点（\(Y = 0\)）より上では、潜在変数 (\(Y*\)) と観測変数 (\(Y\)) が一致しています。
• 切断点より下では、観測変数 (\(Y\)) は全て\(0\)になっています。

→これは、負の値が観察されないことを示しています。

トービットモデルの仮定

ここでは、モデルの前提とされている仮定を紹介しておきます。

誤差項の正規性

$$\varepsilon \sim N(0, \sigma^2)$$

誤差項の同分散性

$$\text{Var}(\varepsilon|x) = \sigma^2$$

説明変数の外生性

$$E(\varepsilon|x) = 0$$

これらが認められないデータの場合は、

• モデルの予測精度が低下する
• 推定値にバイアスが生じる
• 推定量の効率性が低下する
• 標準誤差の推定が不正確になる

といった問題が起きる可能性があります。

この辺りが参考になります。

---

トービットモデルの確率密度関数について

さて、統計検定準一級では、トービットモデルは確率密度関数と分布関数の理解が問われる傾向にあります。

${y_i* > 0}$ の場合の確率密度関数

${y_i* > 0}$ のとき、${y_i (= y_i*)}$ の確率密度関数は次のようになります

$${f(y_i) = \frac{1}{\sqrt{2\pi\sigma}} \exp \left[-\frac{1}{2}\left(\frac{y_i – (\beta_0 + \beta_1x_i)}{\sigma}\right)^2\right]}$$

これは正規分布の確率密度関数の形をしています。

標準正規分布を用いた表現

標準正規分布の確率密度関数を ${\phi(x)}$ とすると、上の ${y_i}$ の確率密度関数は次のように表せます

$${f(y_i) = \frac{1}{\sigma}\phi\left(\frac{y_i – (\beta_0 + \beta_1x_i)}{\sigma}\right)}$$

この表現は、標準化された変数 ${\frac{(y_i – (\beta_0 + \beta_1x_i))}{\sigma}}$ に対する標準正規分布の密度関数を${\sigma}$で割ったものになっています。

${y_i* ≤ 0}$ となる確率

${y_i*}$ が ${0}$ 以下となる確率は、${y_i*}$ の確率密度関数を使って次のように表せます

$${P(y_i^* \leq 0) = \int_{-\infty}^0 \frac{1}{\sigma}\phi\left(\frac{y – (\beta_0 + \beta_1x_i)}{\sigma}\right) dy}$$

これは、${y_i*}$ が ${0}$ 以下となる領域での積分を表しています。

積分の置換

上の被積分関数 ${\phi(・)}$ のかっこ内を ${z}$ と置換すると、次のようになります

$${ \int_{-\infty}^{-\frac{\beta_0 + \beta_1x_i}{\sigma}} \phi(z)dz = \Phi\left(-\frac{\beta_0 + \beta_1x_i}{\sigma}\right) }$$

ここで、Φ(・) は標準正規分布の累積分布関数を表します。

これらの式は、トービットモデルにおける観測値の分布と、切断点（この場合は0）以下となる確率を表現しています。

さて、二つの場合の累積分布関数の積を作り、尤度関数を作りましょう。

$$\prod_{i:y_i>0} \frac{1}{\sigma}\phi\left(\frac{y_i – (\beta_0 + \beta_1x_i)}{\sigma}\right) \times \prod_{i:y_i=0} \Phi\left(-\frac{\beta_0 + \beta_1x_i}{\sigma}\right)$$

尤度関数は、観測されたデータが得られる確率を、モデルのパラメータの関数として表したものです。

1. 左側の項 $\prod_{i:y_i>0} \frac{1}{\sigma}\phi\left(\frac{y_i – (\beta_0 + \beta_1x_i)}{\sigma}\right)$
   • ${y_i > 0}$ となるすべてのiに対する確率密度関数の積です。
   • ${\phi(・)}$は標準正規分布の確率密度関数です。
2. 右側の項 $\prod_{i:y_i=0} \Phi\left(-\frac{\beta_0 + \beta_1x_i}{\sigma}\right)$
   • ${y_i = 0}$ となるすべてのiに対する累積分布関数の積です。

---

補足｜トービットモデルの限界効果について

ここでは限界効果を扱います。

計量経済学だと馴染み深い考え方かもしれませんね。

限界効果の実践的な意味としては、説明変数の微小な変化が従属変数の期待値に与える影響です。ある政策変数の変化が結果変数に与える影響を評価する際、単純に係数を見るだけでは不十分で、限界効果を考慮する必要があります。

政策評価や予測において重要ですね。

条件付き期待値について

限界効果を理解するためには、まず条件付き期待値を考える必要があります。

トービットモデルにおける条件付き期待値は以下のように表されます

$$E[y|x] = \Phi\left(\frac{\beta’x}{\sigma}\right)(\beta’x) + \sigma\phi\left(\frac{\beta’x}{\sigma}\right)$$

• $\Phi(\cdot)$ は標準正規分布の累積分布関数
• $\phi(\cdot)$ は標準正規分布の確率密度関数
• $\beta$はパラメータベクトル
• $x$ は説明変数ベクトル
• $\sigma$ は誤差項の標準偏差

限界効果は、この条件付き期待値を説明変数で偏微分することで得られます

$$\frac{\partial E[y|x]}{\partial x_j} = \beta_j \Phi\left(\frac{\beta’x}{\sigma}\right)$$

この式は、説明変数 $x_j$ の微小な変化が従属変数 $y$ の期待値に与える影響を表しています。

しばしば平均限界効果（Average Marginal Effect, AME）が用いられます。

これは、全てのサンプルについて限界効果を計算し、その平均を取ったものです

$$AME = \frac{1}{n} \sum_{i=1}^n \beta_j \Phi\left(\frac{\beta’x_i}{\sigma}\right)$$

ただし、誤差項の正規性や同分散性の仮定など、モデルの前提条件に注意を払う必要があります。