ゼロ過剰ポアソン分布（ZIP分布）をわかりやすく解説

ゼロ過剰ポアソン分布とは

カウントデータ（離散的な非負整数値）を分析する際、ポアソン分布がよく使用されます。

しかし、実際のデータでは「0」の観測値が理論上の予測よりも多く出現することがあります。このような現象に対応するために考案されたのが、ゼロ過剰ポアソン分布（Zero-Inflated Poisson distribution: ZIP分布）です。

ポアソン分布については、この辺が参考になります。

ZIP分布は、統計検定一級の過去問とかで見かけた方も多いと思います。

ゼロ過剰ポアソン分布は、通常のポアソン分布に「構造的なゼロ」を組み込んだ混合分布モデルです。

ちょっと図で見てみましょう。

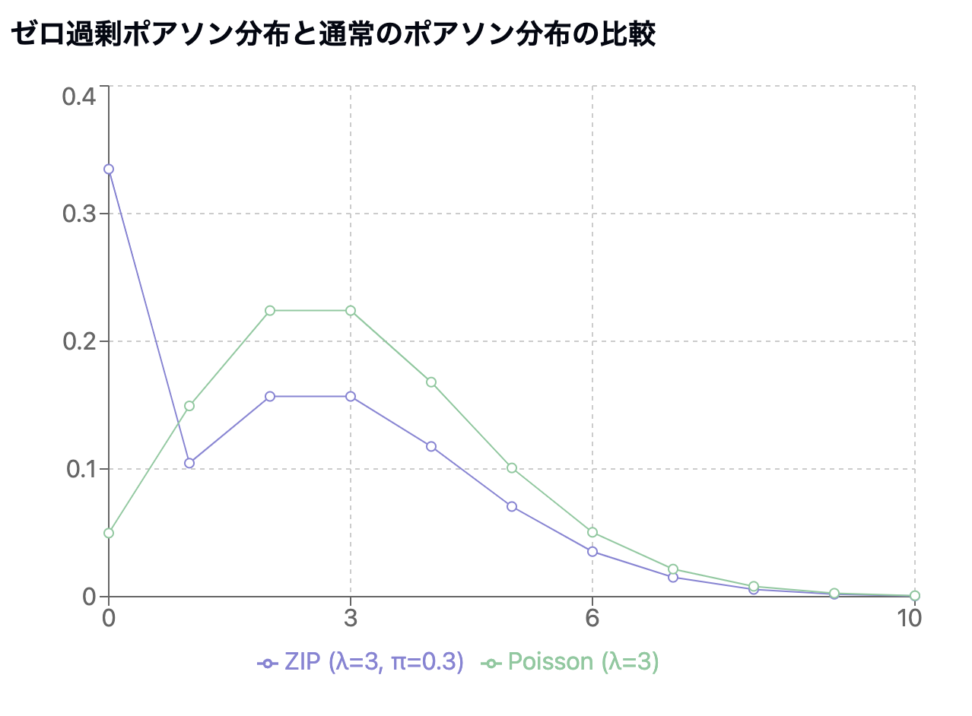
こんな感じで、ゼロの度数が大きいのが特徴です。

データが2つの異なるプロセスから生成されると仮定します

1. 確率${\pi}$で必ず0が生成されるプロセス
2. 確率${(1-\pi)}$でポアソン分布に従うプロセス

加えて、モデルには、以下が仮定されます。

• 過剰なゼロが存在する
• 非ゼロのデータがポアソン分布に従う
• 観測値が互いに独立

確率質量関数

ゼロ過剰ポアソン分布の確率質量関数は以下のように定義されます

$$ P(X = k) = \begin{cases} \pi + (1-\pi)e^{-\lambda} & \text{if } k = 0 \ (1-\pi)\frac{\lambda^k e^{-\lambda}}{k!} & \text{if } k > 0 \end{cases} $$

ここで：

• ${\pi}$は過剰なゼロが生成される確率${（0 ≤ \pi ≤ 1）}$
• ${\lambda}$はポアソン分布のパラメータ（期待値）
• kは観測値

期待値と分散

ZIP分布の期待値と分散は以下のように計算されます

期待値： $$E(X) = (1-\pi)\lambda$$

分散： $$Var(X) = \lambda(1-\pi)(1+\pi\lambda)$$

モデルの推定方法

モデルの推定を行なっていきます。

最尤推定の基本設定

観測データ ${x_1, …, x_n}$ が与えられたとき、ゼロ過剰ポアソン分布の最尤推定を行います。

パラメータ

• $\pi$：ゼロ過剰確率${(0 ≤ \pi ≤ 1)}$
• $\lambda$：ポアソンパラメータ${(\lambda > 0)}$

尤度関数の導出

尤度関数

$$ L(\pi,\lambda|x) = \prod_{i:x_i=0}[\pi + (1-\pi)e^{-\lambda}] \prod_{i:x_i>0}[(1-\pi)\frac{\lambda^{x_i}e^{-\lambda}}{x_i!}] $$

値が1以上かどうかで、項を分けます。

x=0に関しては、ポアソン分布の確率密度関数に${x=0}$を代入することで求められます。

${0!=1}$ですので、分母は省いています。

対数尤度関数

$$ \ell(\pi,\lambda) = \sum_{i:x_i=0}\ln[\pi + (1-\pi)e^{-\lambda}] + \sum_{i:x_i>0}[\ln(1-\pi) + x_i\ln\lambda – \lambda – \ln(x_i!)] $$

EMアルゴリズムによる推定

EMアルゴリズムを使用して最尤推定を行います。

前提として、潜在変数 $Z_i$ を導入し、$Z_i = 1$ のとき構造的ゼロ、$Z_i = 0$ のときポアソン過程からの生成とします。

ゼロ過剰ポアソン分布のパラメータ推定において、EMアルゴリズムは潜在変数を導入することで複雑な最適化問題を扱いやすい形に分解します。

この手法の本質は、観測できない状態（潜在変数）を確率的に推定しながら、モデルのパラメータを段階的に最適化していく点にあります。

先ほど申し上げた通りで、各データポイント $x_i$ に対して、そのデータが構造的なゼロから生成されたのか（$Z_i = 1$）、それともポアソン過程から生成されたのか（$Z_i = 0$）という潜在状態を考えます。

この潜在変数 $Z_i$ の導入により、完全データの対数尤度は以下のように表現されます：

$$ \ell_c(\pi,\lambda|x,z) = \sum_{i=1}^n [z_i\log\pi + (1-z_i)\log(1-\pi) + (1-z_i)(-\lambda + x_i\log\lambda – \log(x_i!))] $$

E-step（期待値計算ステップ）

現在のパラメータ推定値 $\pi^{(t)}$ と $\lambda^{(t)}$ を使用して、潜在変数 $Z_i$ の条件付き期待値を計算します。ここで重要なのは、$x_i = 0$ の場合と $x_i > 0$ の場合で計算が異なる点です。

$x_i = 0$ の場合： $$ \hat{z_i}^{(t+1)} = E[Z_i|x_i=0,\pi^{(t)},\lambda^{(t)}] = \frac{\pi^{(t)}}{\pi^{(t)} + (1-\pi^{(t)})e^{-\lambda^{(t)}}} $$

$x_i > 0$ の場合： $$ \hat{z_i}^{(t+1)} = 0 $$

この計算の背後にある確率的な解釈は以下の通りです。

$x_i = 0$ のデータポイントについて、それが構造的なゼロである事後確率を計算しています。一方、$x_i > 0$ のデータポイントは必然的にポアソン過程から生成されたものであるため、構造的なゼロである確率は0となります。

M-step（最大化ステップ）

M-stepでは、E-stepで計算した潜在変数の期待値 $\hat{z_i}^{(t+1)}$ を用いて、完全データの対数尤度の期待値を最大化します。この最大化問題は、$\pi$ と $\lambda$ について独立に解くことができます。

まず、$\pi$ の更新式は以下のように導出されます

$$ \pi^{(t+1)} = \frac{\sum_{i=1}^n \hat{z_i}^{(t+1)}}{n} $$

この式は、構造的なゼロである期待度数を全データ数で割ったものとして解釈できます。

次に、$\lambda$ の更新式は以下のように導出されます

$$ \lambda^{(t+1)} = \frac{\sum_{i=1}^n x_i}{\sum_{i=1}^n(1-\hat{z_i}^{(t+1)})} $$

この式は、ポアソン過程から生成されたと考えられるデータの平均値を表しています。分母は「ポアソン過程から生成された」と考えられるデータポイントの期待度数の合計です。

さて、上記のステップの前段階で、初期値を以下のように設定して、パラメータを探索していきます。

• $\pi^{(0)}$ を0と1の間の値に設定
• $\lambda^{(0)}$ を標本平均などに基づいて設定