カイ二乗分布とは？正規分布との関わりとわかりやすく解説

カイ２乗分布

カイ二乗分布は連続確率分布の一つです。

この分布は、正規分布に従う独立な確率変数の二乗和によって定義されます。具体的には、自由度${k}$のカイ二乗分布は、${k}$個の独立な標準正規分布 ${N(0, 1) }$に従う確率変数 ${Z_{1}, Z_{2}, …, Z{k}}$について、以下の式で表されます。

$${Z = Z_{1}^2 + Z_2^2 + … + Z_k^k}$$

Zはカイ二乗分布に従う確率変数です。

カイ二乗分布の確率密度関数

カイ二乗分布の確率密度関数は、自由度パラメータ $k$ を持ち、以下のように表されます。

$$
f(x; k) = \begin{cases}
\frac{1}{2^{k/2}\Gamma(k/2)}x^{k/2-1}e^{-x/2}, & x > 0\\
0, & x \leq 0
\end{cases}
$$

• $\Gamma(\cdot)$ はガンマ関数を表します。
• 自由度パラメータ $k$ は正の整数値をとり、分布の形状を決定します。
  • $k$ が大きくなるにつれ、分布は右側に裾が長くなります。

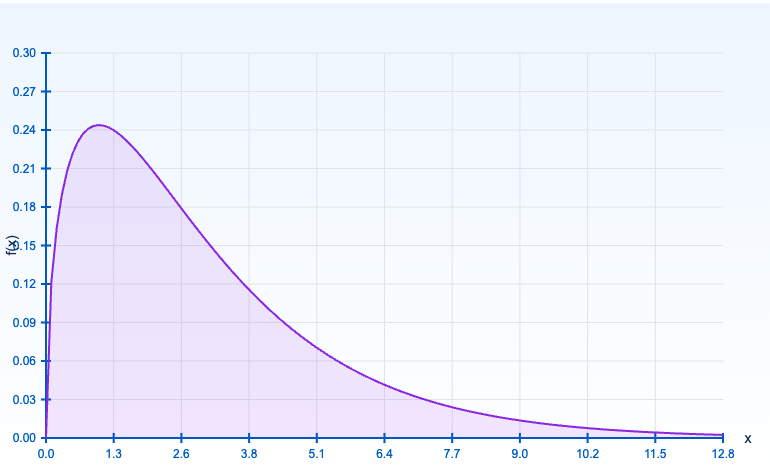
可視化すると上のようになります。

これは自由度３の時の分布です。

ちなみに、自由度2のカイ二乗分布の確率密度関数は、${\lambda=\frac{1}{2}}$の指数分布の確率密度関数と一致します。 これは、自由度2のカイ二乗分布が、2つの独立な標準正規分布に従う確率変数の二乗和として表される一方、${\lambda=\frac{1}{2}}$の指数分布が、単位時間あたり${\frac{1}{2}}$回の事象が発生するポアソン過程における事象間隔を表すことによります。

カイ二乗分布の可視化シミュレーションはこちら。

カイ二乗分布は、t分布やF分布と同じように標本の分布と呼ばれる分布で、確率密度関数を暗記する問いよりも、性質やどの検定に使うか、というのを理解した方が良いです。

他の分布についての記事はこちら。

ガンマ関数ってなに？

ガンマ関数（${Γ(z)}$）は、階乗を複素数領域に拡張した関数であり、以下の積分で定義されます。

$${Γ(z)=\int_0^{\infty}​t^{z−1}e{−t}dt}$$

ガンマ関数は、以下の性質を持ちます。

• ${Γ(z+1) = zΓ(z)}$
• ${Γ(n) = (n-1)! }$（nは自然数）

具体例

例えば、自由度${4}$のカイ二乗分布の確率密度関数は、${Γ(2) = 1! = 1}$ であることを用いて、以下のようになります。

$${f(x) = \frac{1}{2^{\frac{4}{2}}\Gamma(\frac{4}{2})} x^{\frac{4}{2}-1} e^{-\frac{x}{2}} = \frac{1}{4} x e^{-\frac{x}{2}}}$$

特徴｜再生性

また特徴として、再生性があります。

例えば、もし二つの確率変数 ${W_1}$ と${W_2}$ が互いに独立であり、それぞれがカイ二乗分布 ${χ^2(n_1)}$ および ${χ_2(n_2)}$ に従う場合、この二つの確率変数の和 ${W₁ + W₂}$ は自由度 ${n₁ + n₂}$ のカイ二乗分布に従います。

ポアソン分布などの確率分布も再生性を持っています。

カイ二乗分布と他の確率分布との関係

先ほども記載した通り、カイ二乗分布は、$n$ 個の標準正規分布に従う独立な確率変数 $Z_1, Z_2, \ldots, Z_n$ の二乗和から導出されます。

$${X = \sum_{i=1}^n Z_i^2}$$

とすると、$X$ はカイ二乗分布に従い、自由度は $n$ となります。

正規分布 ${N(\mu, \sigma^2)}$ の場合、${\mu}$が${0}$で${\sigma}$が${1}$のとき、標準正規分布になります。この標準正規分布の独立なサンプルを二乗したものを合計することにより、カイ二乗分布が成立します。

また、カイ二乗分布は正規分布の二乗に比例するため、正規分布の確率の計算においても役立ちます。

正規分布の確率密度関数を $\phi(x)$ とすると、

$${x^2 \phi(x) \propto \chi^2_1(x)}$$

の関係があります。

詳しくはこちらの記事をご覧ください。

カイ二乗分布の使い道

さて、このセクションでは分布の性質や使い道を扱います。

標本分散とカイ二乗分布の関係

母集団が正規分布に従う場合、標本分散とカイ二乗分布の間には以下の関係が成り立ちます。

$${\frac{(n-1)s^2}{\sigma^2}\sim\chi^2(n-1)}$$

• $ \sigma^2 $ は母分散
• $ \chi^2(n-1) $ は自由度 ${n−1}$ のカイ二乗分布

この関係は、標本分散に ${(n−1)/\sigma^2}$ を乗じたものが、自由度 ${n−1}$ のカイ二乗分布に従うことを示しています。この性質を利用することで、母分散の区間推定や検定を行うことができます。

具体例

1. 自由度 n−1=9 のカイ二乗分布表から、95%信頼区間の境界値を求めます。
2. 以下の式を用いて、母分散の信頼区間を計算します。

$${\frac{(n-1)s^2}{\chi_{α/2}^2​(n−1)}≤\sigma^2≤\frac{(n-1)s^2}{\chi_{1-α/2}^2​(n−1)}}$$

カイ二乗検定

また、カイ二乗分布は適合度の良さの検定や独立性の検定などで使われる、カイ二乗値の分布を記述するためにも用いられます。

観測度数 $O_i$ と期待度数 $E_i$ の差の二乗の総和を、期待度数で割ったものが、\[\sum_{i=1}^k \frac{(O_i – E_i)^2}{E_i}\]であり、これはカイ二乗分布に従うことが知られています。

$${\sum_{i=1}^k \frac{(O_i – E_i)^2}{E_i} \sim \chi^2_{k-p-1} }$$

• $k$ はカテゴリ数
• $p$ は推定されるパラメータ数

この検定に限らず、自由度ってどう計算するっけ？？と勘違いするポイントなので、注意してくださいね。