【Transformer】ソフトマックス関数についてわかりやすく解説｜python
こんにちは、青の統計学です。
今日は、GPT等の生成AIモデルでも使われているtransformerの中にあるソフトマックス関数についてご紹介いたします。
そのほかの非線形変換について詳しく知りたい方は、以下のコンテンツをご覧ください。
ソフトマックス関数｜softmax function
ソフトマックス関数は、ニューラルネットワークにおいてよく使われる活性化関数の一つです。
主に多クラス分類問題において出力層で使用されます。
ソフトマックス関数は、入力された値を確率分布として扱うために使用され、各クラスに属する確率を出力します。
ソフトマックス関数は以下の式で表されます。
$$f_i(x)=\frac{e^{x_i}}{\sum _{k=1}^n e^{x_k}}$$
ここで、\(z\)は入力ベクトルであり、\(z_i\)はその中の \(i\)番目の要素です。
\(K\)はクラスの数を表します。
この関数は、入力 \(z\) を \(K\)個のクラスに対する確率分布に変換します。
#softmax function
def softmax(x,axis=1):
x -= x.max(axis,keepdims=True) # expのoverflowを防ぐ
x_exp = np.exp(x)
return x_exp / x_exp.sum(axis,keepdims=True)で、目的関数は基本的に多クラス交差エントロピー誤差関数を使います。
クロスエントロピーとも言いますね。
$$E(\mathbf{x}, \mathbf{y} ; \mathbf{W}, \mathbf{b})=-\frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K \mathbf{y}_{i,k}\log \hat{\mathbf{y}}_{i, k}\left(\mathbf{x}_i ; \mathbf{W}, \mathbf{b}\right)$$
モデルの推論は、入力ベクトル\(x\)に更新される重みパラメータ\(W\)と\(B\)を用いて行います。
$$\hat{y}_i=softmax(Wx_i+b)$$
別の言い方で言うとソフトマックス回帰は，ロジスティック回帰を多クラス分類に拡張したものです。
ソフトマックス関数の特徴
確率分布の形成
ソフトマックス関数は、入力を各クラスに対する確率分布に変換します。
これにより、モデルの出力をクラスごとの確率として解釈できます。
出力の総和が1
ソフトマックス関数の出力の総和は1になります。
したがって、出力は確率として解釈できます。この性質は多クラス分類問題で特に重要です。
非線形性
ソフトマックス関数は非線形関数であり、ニューラルネットワークの非線形性を担います。
これにより、モデルがより複雑なパターンを学習できます。
勾配の計算が容易
ソフトマックス関数の微分は比較的簡単に計算できます。
これは、勾配降下法などの最適化アルゴリズムで重要です。
さて、ちょっと深掘りしてみましょう。
ソフトマックス関数の微分を計算する際には、通常、次のような形で表現されます
$$\begin{equation}
\frac{\partial softmax(z)i}{\partial z_j}=\frac{\partial}{\partial z_j}\left(\frac{e^{z_i}}{\sum{k=1}^K e^{z_k}}\right)
\end{equation}$$
この微分を計算するために、 \(i=j\)の場合と \(i≠j\) の場合に場合分けします。
①\(i=j\)の場合
$$\frac{\partial softmax(z)_i}{\partial z_j}=\frac{e^{z_i} \sum_{k=1}^K e^{z_k}-e^{z_i} e^{z_j}}{\left(\sum_{k=1}^K e^{z_k}\right)^2}$$
これを整理すると、\(softmax(z)i\)の微分は以下のようになります。
$$\frac{\partial softmax(z)_i}{\partial z_j}=softmax(z)_i(1-softmax(z)_i)$$
②\(i≠j\) の場合
$$\frac{\partial softmax(z)_i}{\partial z_j}=-\frac{e^{z_i} e^{z_j}}{\left(\sum_{k=1}^K e^{z_k}\right)^2}$$
$$\frac{\partial softmax(z)_i}{\partial z_j}=-softmax(z)_i*softmax(z)_j$$
つまり、ソフトマックス関数の勾配計算が比較的簡単である理由は、その微分がソフトマックス関数自体で表現できるため、ですね！！
具体的には、ソフトマックス関数の微分を計算する際に、ソフトマックス関数の出力を利用することで勾配を簡単に求めることができました。
Query-Key-Valueを用いたAttention機構について（Transformer）
昨今の生成AIのブームに寄った話をすると、トランスフォーマーのアルゴリズムの中でソフトマックス関数が使われています。
Transformerでは、QueryとKey-Valueペアを用いて出力をマッピングする Scaled Dot-Product Attention（スケール化内積Attention）という仕組みを使っています。
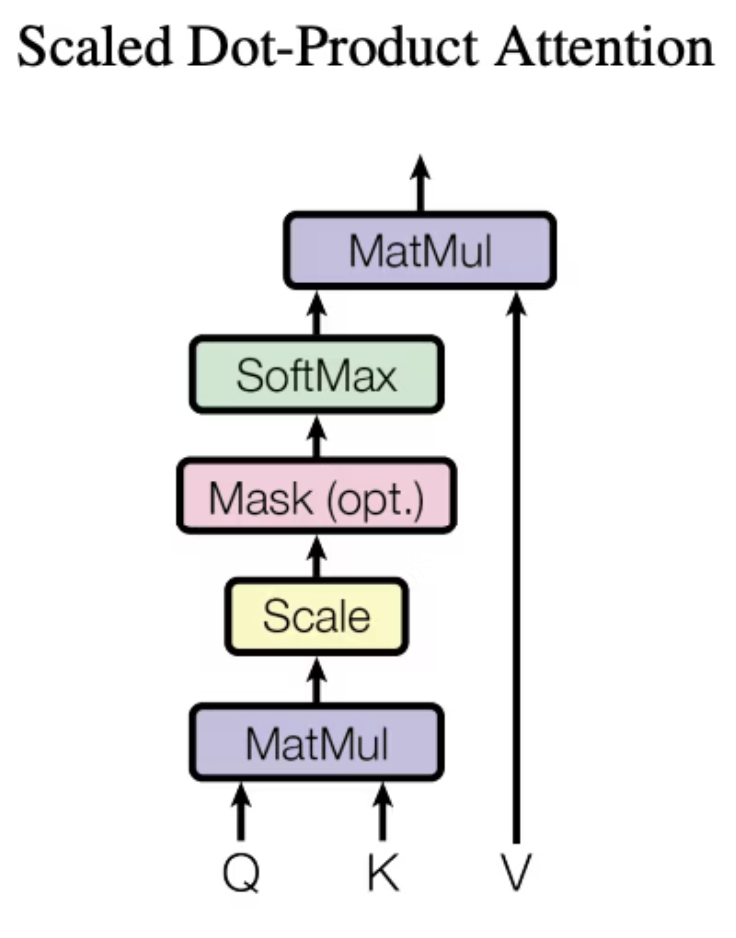
図のQはQuery、KはKey、VはValueです。
Queryは探索対象、Key-Valueは探索の元データで、探索用途のKeyと本体のValueに分離することでより高い表現力を得ることができます。
Query（クエリ)
クエリは、アテンションメカニズムにおいて注目の焦点となる情報を表します。
つまり、クエリは「何に注目すべきか」という情報を提供します。
トランスフォーマーのコンテキストでは、クエリは一般的に入力系列の各要素に対応し、注意の対象となるトークンを示します。
数学的に表すと、クエリ\(Q\) は次のように表されます
$$Q=XW_Q$$
ここで、\(X\) は入力（通常はエンコーダーの出力）、\(W_Q\)はクエリ行列の重み行列です。
Key（キー）
キーは、クエリとの関連性を計算するための情報を提供します。
キーは通常、入力系列の各要素に対応し、その要素がクエリとどの程度関連性があるかを示します。
数学的に表すと、キー \(K\) は次のように表されます
$$K=XW_K$$
ここで、\(X\)は入力（通常はエンコーダーの出力）、\(W_K\)はキー行列の重み行列です。
Value（値）
値は、クエリに関連付けられる情報を提供します。
値は通常、入力系列の各要素に対応し、その要素がクエリに対してどのような情報を持っているかを示します。
数学的に表すと、値 \(V\)は次のように表されます
$$V=XW_V$$
ここで、\(X\)は入力（通常はエンコーダーの出力）、\(W_V\)はvalue行列の重み行列です。
これらの行列\(W_V,W_K,W_K\)は、モデルの学習によって更新されるパラメータです。
このようにQuery、Key、Valueおよび出力は全てベクトルで、出力はValueの重み付き和として計算されます。
各Valueに割り当てられる重みは、Queryと対応するKeyの類似度から計算されます。
ソフトマックス関数は以下のように類似度の計算で使われています。
$$Attention(Q, K, V ) = softmax\Bigl(\frac{QK^T}{\sqrt{d_k}}\Bigr)V$$
さて、具体で言うとソフトマックス関数は正規化のために使われています。
QueryとKeyの要素毎の内積を算出してSoftmaxで正規化します。
内積をそのまま正規化するとQueryとKeyの次元数\(d_k\)が大きくなるほどSoftmaxのlogitが飽和してしまう為、\(\sqrt{d_k}\)で除算することで勾配消失を防ぎます。
このようにしてQueryに関する情報をKeyとの関連度から検索して、モデルが長距離の依存関係を学習することが可能になります。
自然言語処理での利用例はこちらをどうぞ
