【仮説検定】第1種の過誤と第2種の過誤とは？

こんにちは、青の統計学です。

今回は、統計検定2級で頻出の「第一種の過誤(type I error)と第二種の過誤(type II error)」について解説します。

こちらの動画では、もっと簡単に解説しています。

前提｜統計的仮説検定とは何か？

第1種の過誤と第2種の過誤を理解する前に、まずは統計的仮説検定の基本的な考え方を押さえておきましょう！

統計的仮説検定とは、私たちが知りたいこと（例えば「新しい広告キャンペーンは売上を増加させたか？」）について、データを使って統計的に正しそうと言えるかどうかを判断する枠組みのことですね。

統計的仮説検定では、まず2つの仮説を設定します。

• 帰無仮説（Null Hypothesis, $H_0$）
  • 「差がない」「効果がない」「関係がない」といった、現状維持や否定的な立場を示す仮説です。例えば、「新しい広告キャンペーンは売上を増加させない」といった仮説がこれにあたります。
• 対立仮説（Alternative Hypothesis, $H_1$）
  • 帰無仮説と対立する仮説で、私たちがデータから証明したいこと、つまり「差がある」「効果がある」「関係がある」といった仮説です。例えば、「新しい広告キャンペーンは売上を増加させる」といった仮説がこれにあたります。

で、集めたデータが帰無仮説を「棄却」する（つまり「間違いだ」と判断する）のに十分な証拠となるかどうかを評価します。もしデータが帰無仮説を棄却するほど珍しいものであれば、対立仮説を採択します。しかし、データが帰無仮説を棄却するほど珍しくなければ、帰無仮説を「棄却できない」と判断します。

とはいえ、「棄却できない」は帰無仮説が正しいことを意味しないです。

第1種の過誤とは？

第1種の過誤とは、帰無仮説が本当は正しいにもかかわらず、誤ってこれを棄却し、対立仮説を採択してしまうという種類の誤りです。

例えば、「この薬には効果がない」という帰無仮説が本当は正しいのに、「効果がある」と誤って判断してしまうケースです。この誤りを犯す確率は、通常、有意水準（Significance Level）と呼ばれ、${ \alpha }$（アルファ）で表されます。統計的仮説検定を行う際、この${ \alpha }$の値を事前に設定します。

有意水準と棄却域

有意水準${ \alpha }$は、第1種の過誤を犯すことを許容する確率の上限を示します。つまり、帰無仮説が正しいという前提のもとで、観測されたデータがどれくらい珍しい場合に帰無仮説を棄却するか、その基準を定めているというわけで、この「珍しさ」の基準となる範囲を棄却域と呼びます。

例えば、ある検定統計量（データから計算される値と理解してください）が、帰無仮説のもとではほとんど出現しないような極端な値を取った場合、その値は棄却域に入ると判断され、帰無仮説は棄却されます。

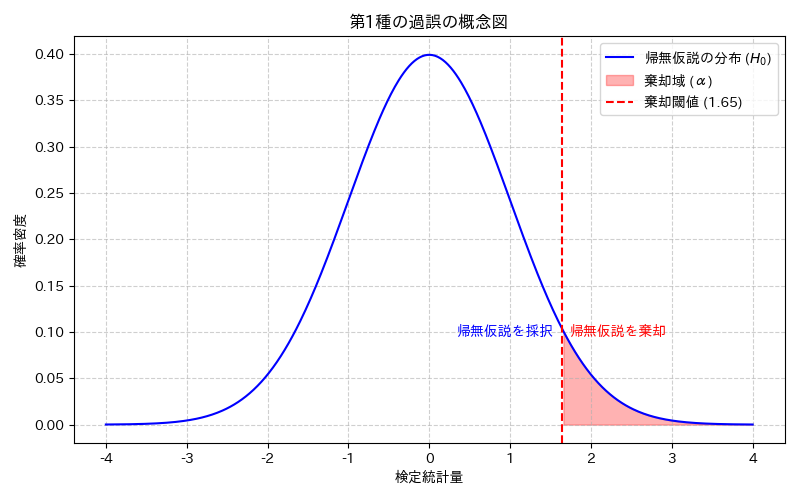
具体例

検出力と標本サイズ

第1種の過誤の確率は有意水準${ \alpha }$によって直接制御されますが、この${ \alpha }$と密接に関わるのが検出力です。検出力とは、帰無仮説が本当は間違っているときに、正しくそれを棄却できる確率のことです。つまり、対立仮説が正しい場合に、その正しさをきちんと「検出」できる能力を指します。

第1種の過誤の確率${ \alpha }$を小さく設定する（つまり、より慎重に判断する）と、帰無仮説を棄却しにくくなるため、検出力は一般的に低下します。

また、標本サイズも第1種の過誤と検出力に影響を与えます。標本サイズを大きくすると、より多くの情報を得られるため、データのばらつきが小さくなり、より正確な推定や検定が可能になります。これにより、同じ有意水準${ \alpha }$を保ちながら、検出力を高めることができます。つまり、より多くのデータがあれば、誤った判断を減らしつつ、正しい判断を下せる確率も上げられる、ということですね。

第2種の過誤とは？

第2種の過誤とは、帰無仮説が本当は間違っている（つまり対立仮説が正しい）にもかかわらず、誤ってこれを棄却できず、帰無仮説を採択してしまうという種類の誤りです。これは、いわば「真犯人を見逃してしまう」ような状況に例えられます。例えば、「この薬には効果がある」という対立仮説が本当は正しいのに、「効果がない」と誤って判断してしまうケースです。この誤りを犯す確率は、通常、${ \beta }$（ベータ）で表されます。

ここまでの内容を表にして表すとこの通りです。

帰無仮説	棄却する	棄却できない
真	type I error	○
偽	○	type II error

機械学習でも使う混合行列にも同じ考えを適用しています。

詳しくは、【多変量解析】ROC曲線とAUCによる判別分析|pythonをご覧ください。

ベータエラーと検出力

さて、第2種の過誤の確率${ \beta }$は、対立仮説が正しいという前提のもとで、観測されたデータが帰無仮説を棄却するほど「珍しくない」と判断されてしまう確率でした。

先ほども触れましたが、検出力（Power）は${ 1 – \beta }$で表されます。つまり、第2種の過誤を犯す確率${ \beta }$が小さければ小さいほど、検出力は高くなります。これは、本当に効果があるものを見逃すリスクが減り、正しく効果を検出できる確率が高まることを意味します。

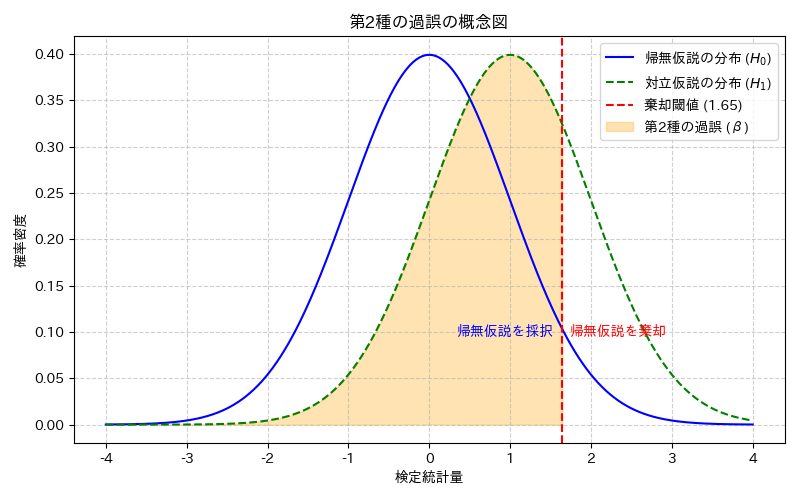
さらに知ってほしい概念として、効果量（Effect Size）があります。効果量とは、帰無仮説と対立仮説の間に「どれくらいの差があるか」を示す指標です。

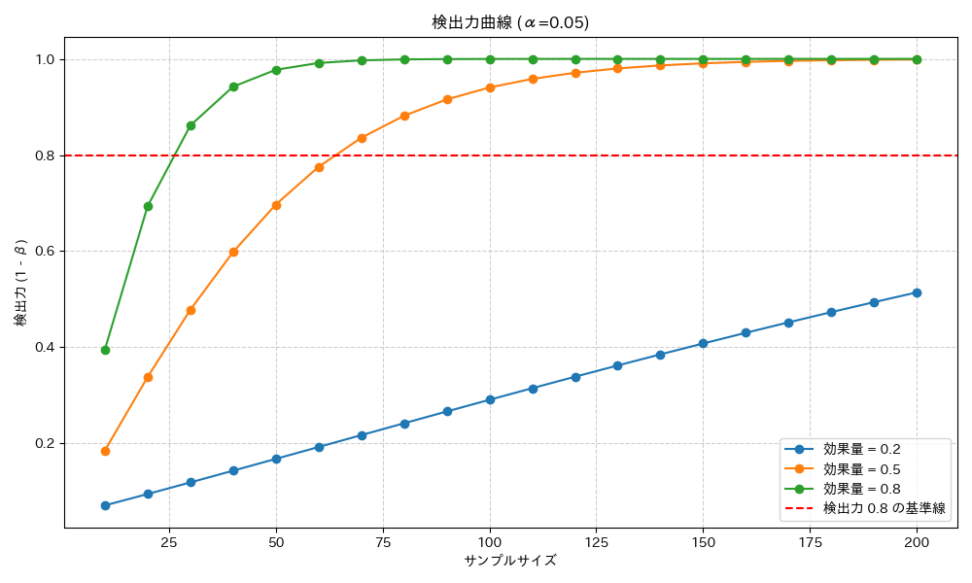
例えば、新しい薬が既存の薬に比べて「どれくらい効果があるか」を具体的な数値で表したものです。効果量が大きい（つまり、帰無仮説と対立仮説の差が大きい）ほど、その差をデータから検出しやすくなるため、検出力は高まります。逆に、効果量が小さい（差がわずかしかない）場合、そのわずかな差を検出するためには、より大きな標本サイズが必要になります。

効果量と標本サイズ

第2種の過誤、検出力、標本サイズ、そして効果量は、互いに密接に関連し合う四つの要素です。これらは「検出力分析（Power Analysis）」と呼ばれる手法で、検証設計の段階で用いられます。例えば、「これくらいの効果量（期待される差）を、これくらいの検出力（見逃さない確率）で検出したい場合、どれくらいの標本サイズが必要か？」といった問いに答えるために使われます。この関係性は、以下のようにまとめられます。

トレードオフと最適化

ここまで見てきた通り、第1種の過誤と第2種の過誤は、多くの場合、トレードオフの関係にあります。つまり、一方の過誤を減らそうとすると、もう一方の過誤が増えてしまう傾向があります。

具体的には、第1種の過誤の確率である有意水準${ \alpha }$を小さく設定する（例えば、0.05から0.01へ）と、帰無仮説を棄却する基準がより厳しくなります。これは、誤って「ある」と判断してしまうリスクを減らすことにつながります。しかし、その結果として、本当に「ある」ものを見逃してしまう、つまり第2種の過誤を犯す確率${ \beta }$が増加し、検出力（${ 1 – \beta }$）が低下してしまうのです。

逆に、第2種の過誤の確率${ \beta }$を小さくしようとすると（つまり検出力を高めようとすると）、第1種の過誤の確率${ \alpha }$が増加する傾向があります。これは、より積極的に「ある」と判断しようとするため、誤って「ある」と判断してしまうリスクも高まるからです。

実務でどう調整する？

ぶっちゃけ、統計的検定を意識せずに、効果が出たかどうかを判断していたり、代々伝わるよく分からないエクセルファイルで有意差をチェックしていたりする現場がほとんどなので、上で解説したエラーを理解して上で意思決定するだけでも十分価値があると思います。

。。。その上で、トレードオフの関係の中で、どうαとβを調整するのか考えてみましょう。

結論、状況と目的によって異なります。

例えば、以下のようなケースが考えられます。

• 第1種の過誤を厳しく抑えたいケース
  • 新薬の承認、製品の安全性検査など、誤って「安全」や「効果あり」と判断することが重大な結果を招く場合。この場合、${ \alpha }$を小さく設定し、第1種の過誤のリスクを最小限に抑えることを優先したいはず。
• 第2種の過誤を厳しく抑えたいケース
  • 初期段階の研究、スクリーニング検査など、重要な発見を見逃したくない場合。この場合、検出力を高めるために${ \beta }$を小さくすることを優先します。ただし、その分、第1種の過誤のリスクは高まることを許容します。

繰り返しになりますが、このトレードオフを乗り越え、両方の過誤を同時に減らす方法は、標本サイズを増やすことです。標本サイズを大きくすることで、データの情報量が増え、より正確な判断が可能になるため、有意水準${ \alpha }$を維持したまま検出力を高めることができます。

おまけ｜最強力検定

2つの過誤の確率や検出力についての理解が深まった方に、いくつか検定方法をご紹介します。まずは、最強力検定です。

最強力検定とは、「有意水準が同一のもとで、ある検定Fとある検定Gの検出力1-βを比べた時、Fの方が大きい時」に、「FはGより強力」であると言います。

つまり検定として優れているということになります。

当然他の条件が正しく、有意水準が一定以下なら、検出力は高ければ高いほど良いです。

帰無仮説と対立仮説がどちらも単純仮説(パラメータが一つ)の時、検出力を最大にする最強力検定が存在します。

これを、ネイマン・ピアソンの補題と言います。

Neyman-Pearsonの仮説検定

ここまでの話で、第一種の過誤と第二種の過誤はトレードオフの関係にあることが理解できたと思います。

このことから、一般的な仮説検定では第一種の過誤の大きさにのみ注目します。どちらの過誤も避けるのは現実的に難しいからです。この検定を、ネイマン・ピアソンの仮説検定と呼びます。

第一種の過誤の大きさに注目する以上、帰無仮説が棄却できない時には「結論が言えない」というデメリットがあります。例えば、帰無仮説が棄却できない時は、「帰無仮説が正しい」とは言えません。

あくまで、「現在設定した有意水準では、帰無仮説と対立仮説は正しいとも正しくないとも言えない」という結論にしかなりません。ここまでの説明で、「ネイマンピアソンの仮説検定は、モデル同士を比較する多くの方法のうち一つでしかない」と理解いただけたかと思います。

他のモデルの比較に関しては、以下のコンテンツをご覧ください。

有意水準とp値について復習したい方はこちらをご覧ください。

【仮説検定】p値をゼロから解説(第一種の過誤,第二種の過誤,検出力)