信頼区間と信用区間の違いをわかりやすく解説
信頼区間と信用区間
母集団のパラメータを推定する際に用いられる「信頼区間」と「信用区間」は、どちらもある範囲内に真の値が含まれる確率を示す概念ですが、その解釈や計算方法に大きな違いがあります。
詳しく見ていきましょう。
HPD区間やベイズ統計学の復習がしたい方はこちらの記事がオススメです。
信頼区間
まず、信頼区間について説明します。
母集団の未知のパラメータ $\theta$ を推定するために、$n$ 個のランダムサンプル $X_1, X_2, \ldots, X_n$ から点推定量 $\hat{\theta}$ が計算されます。

点推定量は母集団パラメータの単一の値の推定値ですが、サンプリング誤差のため、当然真の値と一致するとは限りませんね。
そこで、信頼区間は $\hat{\theta}$ の周りの範囲を提供し、この範囲内に真の母集団パラメータ $\theta$ が含まれる確率を指定します。
信頼区間は、以下の形で表されます。
$$\hat{\theta} \pm z_{\alpha/2} \cdot \text{SE}(\hat{\theta})$$
$z_{\alpha/2}$ は標準正規分布の上側 $\alpha/2$ 分位点、$\text{SE}(\hat{\theta})$ は $\hat{\theta}$ の標準誤差です。
この式は、点推定値 $\hat{\theta}$ の周りの範囲を定義し、その範囲内に真の母集団パラメータ $\theta$ が含まれる確率が $(1 – \alpha)$ になることを意味します。
通常、$\alpha$ は 0.05 または 0.01 に設定され、対応する信頼水準は 95% または 99% となります。
この辺りは統計検定2級では頻出の部分ですね。
具体例を挙げてみましょう。
$n$ 個のランダムサンプル $X_1, X_2, \ldots, X_n\sim N(\mu,\sigma^2)$ から母集団平均 $\mu$ の点推定量 $\bar{X}$ を計算したとします。
このとき、$\bar{X}$ の標準誤差は $\text{SE}(\bar{X}) = \sigma / \sqrt{n}$ です (ここで $\sigma$ は母集団の標準偏差)。
有意水準 $\alpha = 0.05$ のとき、$z_{0.025} = 1.96$ なので、95% 信頼区間は次のように計算されます。
$$\begin{equation*}
\bar{X} \pm 1.96 \cdot \frac{\sigma}{\sqrt{n}}
\end{equation*}$$
信頼区間の解釈
信頼区間の解釈
信頼区間95%:「もし同じ実験を何度も繰り返した場合、95%の信頼区間が真の値を含む確率は95%である」と解釈されます。
あくまで、確率の対象は「信頼区間」であり、「母集団平均${\mu}$」ではありません。
母集団平均${\mu}$は、ある一定の値であり、確率的に変動するものではありません。
上でもランダムサンプリングや標準誤差の話をしました通り、信頼区間は、実験を何度も繰り返すという仮想的状況に基づいて解釈されるものであり、当然ですが毎回の繰り返しで、異なる標本が得られ、異なる信頼区間が計算されます。
なので、この範囲内に真の母集団平均 $\mu$ が含まれる確率は 95% となります、というのは誤解を招く表現ですね。
具体例
例えば、ある商品の重量の平均を調べたいとします。100個の商品を抽出して重量を測定し、95%信頼区間を計算したとします。このとき、計算された信頼区間に真の平均重量が含まれているかどうかは、この1回の調査では分かりません。しかし、同じ実験を100回繰り返せば、約95回の信頼区間に真の平均重量が含まれることが期待されます。
信用区間
一方、信用区間は、ベイズ統計学における概念です。
事前分布と尤度関数から得られる事後分布を使用して、母集団パラメータの credible interval (信用区間)を構築します。
信用区間は、母集団パラメータが特定の範囲内に含まれる事後確率を提供します。
事後分布 $p(\theta | x)$ に対して、$\int_a^b p(\theta | x) \, d\theta = 1 – \alpha$ を満たす範囲 $[a, b]$ が信用区間となります。
つまり、母集団パラメータ $\theta$ がこの範囲内に含まれる事後確率は $(1 – \alpha)$ です。
数学的には、信用区間は次のように表すことができます
$$
{\int_a^b p(\theta | x) \, d\theta = \alpha}
$$
たとえば、正規分布の平均 $\mu$ に対する事後分布が $\mathcal{N}(\mu_0, \sigma_0^2)$ であれば、$\mu_0 \pm z_{\alpha/2} \sigma_0$ が $(\alpha)$ の信用区間となります。
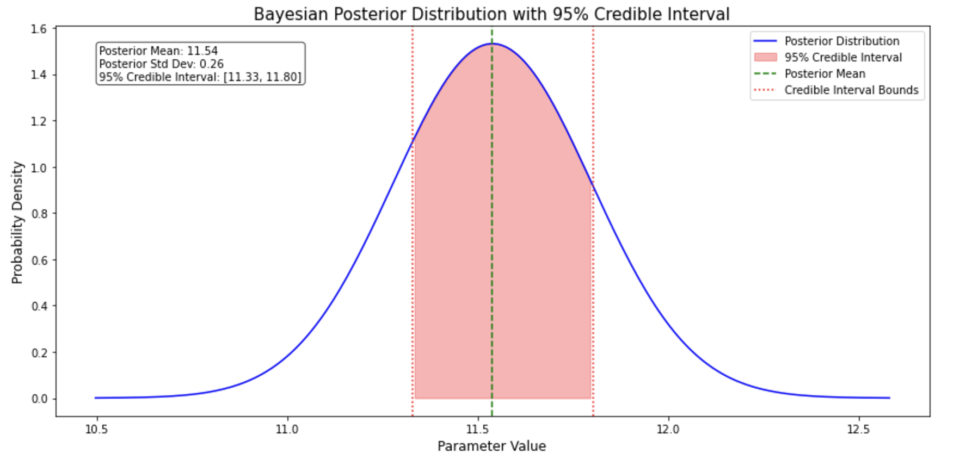
- 青い曲線: 事後分布
- 赤い影: 95%信用区間
- 緑の点線: 事後分布の平均
- 赤の点線: 信用区間の境界
作図をしてみました。
目的は、母集団の平均(母平均)を推定するための典型的なベイズ推論です
事前分布に正規分布を仮定(平均10、標準偏差3)して、十回くらいサンプリングしてみました。
密度が高い部分にフォーカスしている結果、事前分布の平均を信用区間が包含していることがわかりますね。
信用区間の解釈
信用区間の解釈
真の母集団平均μが含まれる確率は〜%と解釈できる。
まず信頼区間の前提と違うのは、母集団平均${\mu}$を確率変数として扱うという点です。
事前分布と尤度関数から事後分布を求めます。
この事後分布は、データを観測した後の${\mu}$についての私たちの「信念」を表す分布でしたね。
95%信用区間は、この事後分布において確率が95%を占める区間として定義されます。
つまり、「このデータを観測した今、μが95%の確率でこの区間にある」と解釈できるのです。
まとめ
さて、ここまでで差は理解できましたでしょうか。

両者の主な違いは、信頼区間が頻度論的アプローチに基づいているのに対し、信用区間がベイズ的アプローチに基づいている点です。
信頼区間は長期的な確率的振る舞いに基づいており、実験や調査を無限に繰り返した場合の範囲を示唆しています。
一方、信用区間はベイズ理論に基づき、具体的なデータに対する事後分布から直接計算されるパラメータの範囲を表しています。
信用区間は事前情報を反映できるため、信頼区間よりも狭い区間を得られる可能性がありますが、事前分布の選択が重要になります。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!





