【確率分布の特徴を知りたい】モーメント法をわかりやすく解説

こんにちは、青の統計学です。

今回は、モーメント法について解説します。

統計検定準１級では、モーメント母関数だったり、モーメント法を使ったシミュレーションの問題が出てきますが、なかなか体系的に学べる機会は少ないので、これを機に学習していきましょう

モーメントとは何か？：確率分布の「形」を捉える概念

まずは、モーメントとは何なのかを理解する必要があります。

平均や分散などの統計量から考えてみましょう。

原点まわりのモーメント

確率変数 $X$ の$k$次原点まわりのモーメント (raw moment) は、その確率変数の $k$ 乗の期待値として定義されます。

数式で表すと以下のようになります。

$${ \mu_k = E[X^k] }$$

この定義から、いくつかの代表的なモーメントを導き出すことができます。

1次原点まわりのモーメント

$k=1$ の場合、${\mu_1 = E[X]}$ となり、これは確率変数 $X$ の期待値そのものです。

つまり、平均は確率分布の重心を示していると解釈できます。

2次原点まわりのモーメント

$k=2$ の場合、${\mu_2 = E[X^2]}$ となります。これは $X$ の2乗の期待値であり、後述する分散の計算に用いられますね。

期待値や分散については、こちらの記事がおすすめです。

期待値と分散について｜確率論と統計学の重要概念をわかりやすく解説

中心モーメント

原点まわりのモーメントが原点（0）を基準にしているのに対し、中心モーメントは、確率分布の平均 ${\mu = E[X]}$ を基準として定義されます。

$k$次中心モーメントは次のように表されます。

$${ \mu_k = E[(X – \mu)^k] }$$

中心モーメントは、分布の形状をより直接的に捉えることができます。

1次中心モーメント

$k=1$ の場合、${\mu_1 = E[X – \mu] = E[X] – \mu = \mu – \mu = 0}$ となります。

まあこれは常に0になるため、分布の形状を特徴づける上ではあまり使われません。

2次中心モーメント

$k=2$ の場合、${\mu_2 = E[(X – \mu)^2]}$ となり、これは確率変数 $X$ の分散そのものです。

要するに、分散とは「データが平均の周りにどの程度散らばっているか」を示すと理解していると思いますが、この説明でよりしっくり来るのではないでしょうか。

つまり、分散は確率分布の広がり具合を定量化しているのですね。

3次中心モーメント: $k=3$ の場合、${\mu_3 = E[(X – \mu)^3]}$ となります。これは確率分布の歪度に関連し、分布の非対称性を示します。

正の値ならば右に裾が長く、負の値ならば左に裾が長い分布であることを意味します。

4次中心モーメント

$k=4$ の場合、${\mu_4 = E[(X – \mu)^4]}$ となります。これは確率分布の尖度に関連し、分布の「とがり具合」や「裾の重さ」を示します。

正規分布と比較して、中央が尖っていて裾が厚いか、あるいは中央が平坦で裾が薄いかを表します。

尖度と歪度については、こちらをご参照ください。

【統計検定2級】歪度と尖度をわかりやすく解説|python

モーメントと期待値、分散、歪度、尖度

ここまでみてきたように、平均、分散、歪度、尖度といった基本的な統計量は、すべてモーメントの特殊なケースとして捉えることができます。特に、平均は1次原点まわりのモーメント、分散は2次中心モーメントですね

これらのモーメントは、確率分布の重心（平均）、広がり（分散）、非対称性（歪度）、とがり具合（尖度）という、その「形」を特徴づける情報を含んでいます。

数式だけだとイメージしづらいので、正規分布と指数分布、一様分布の平均、分散、歪度、尖度を可視化してみました。

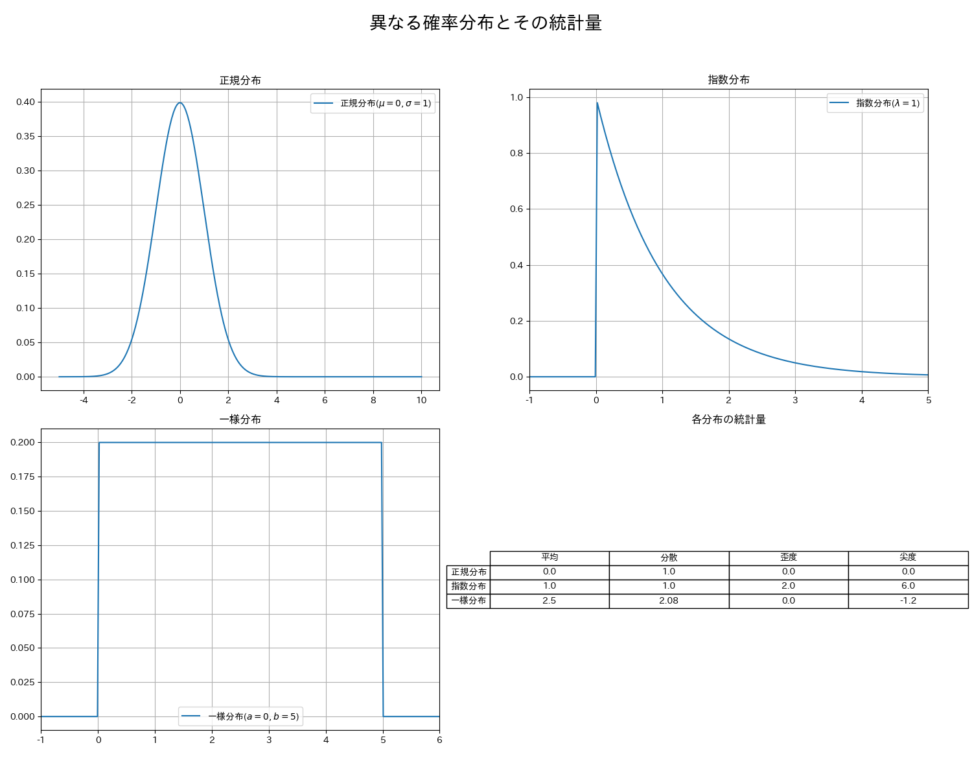
正規分布のバランスの良さがわかるかと思います。

モーメント法の数学的背景：母集団と標本の橋渡し

モーメントのことがわかった上で、いよいよモーメント法について触れていきます。

モーメント法は、母集団の未知のパラメータを推定するための手法です。

母集団モーメントの定義

まず、母集団の確率分布が未知のパラメータ ${\theta = (\theta_1, \dots, \theta_m)}$ に依存すると仮定します。

この母集団の $k$次原点まわりのモーメント $m_k$ は、先ほど定義したように、確率変数 $X$ の $k$ 乗の期待値として表されます。

これは、一般的にパラメータ ${\theta}$ の関数となります。

$${ m_k = E[X^k] = g_k(\theta_1, \dots, \theta_m) }$$

例えば、正規分布 $N(\mu, \sigma^2)$ の場合、パラメータは ${\mu}$ と ${\sigma^2}$ です。

• 1次母集団モーメント: $m_1 = E[X] = \mu$
• 2次母集団モーメント: $m_2 = E[X^2] = \sigma^2 + \mu^2$

これらの母集団モーメントは、母集団全体の性質を表す理論的な値です。

標本モーメントの定義

次に、母集団から抽出された $n$ 個の標本データ ${X_1, X_2, \dots, X_n}$ を考えます。この標本データから計算される $k$次標本モーメント${\hat{m}_k}$ は、標本値の $k$ 乗の平均として定義されます。

$${ \hat{m}_k = \frac{1}{n} \sum_{i=1}^n X_i^k }$$

同様に、いくつかの標本モーメントを導き出すことができます。

1次標本モーメント

$${\hat{m}_1 = \frac{1}{n} \sum_{i=1}^n X_i}$$

これは標本平均そのものですね

2次標本モーメント

$${\hat{m}_2 = \frac{1}{n} \sum_{i=1}^n X_i^2}$$

パラメータ推定のメカニズム

モーメント法の基本的な考え方は、母集団の理論的なモーメント（$m_k$）と、標本から得られた標本モーメント（${\hat{m}_k}$）が、十分に大きな標本サイズにおいて近似的に等しくなるという大数の法則に基づいています。

中心極限定理についてわかりやすく解説｜大数の法則との違い

したがって、未知のパラメータが $m$ 個ある場合、最初の $m$ 個の母集団モーメントを対応する標本モーメントと等しいと仮定し、連立方程式を立てて解くことで、パラメータの推定値を得ます。

$${ \begin{cases}
m_1 = \hat{m}_1 \\
m_2 = \hat{m}_2 \\
\vdots \\
m_m = \hat{m}_m
\end{cases} }$$

できました。

この連立方程式を解くことで得られる ${\theta}$ の推定値を、モーメント推定量と呼びます。

例えば、正規分布 $N(\mu, \sigma^2)$ のパラメータ ${\mu}$ と ${\sigma^2}$ を推定する場合を考えましょう。パラメータは2つなので、1次と2次のモーメントを使います。

1. 母集団モーメント:

$${ m_1 = \mu }$$

$${ m_2 = \sigma^2 + \mu^2 }$$

2. 標本モーメント:

$${ \hat{m}_1 = \bar{X} }$$

$${ \hat{m}_2 = \frac{1}{n} \sum_{i=1}^n X_i^2 }$$

これらを等しいとおくと、

$${ \bar{X} = \mu }$$

$${ \frac{1}{n} \sum_{i=1}^n X_i^2 = \sigma^2 + \mu^2 }$$

この連立方程式を解くと、

$${ \hat{\mu} = \bar{X} }$$

$${ \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n X_i^2 – (\bar{X})^2 = \frac{1}{n} \sum_{i=1}^n (X_i – \bar{X})^2 }$$

となります。

つまり、正規分布のモーメント推定量は、母平均に対しては標本平均、母分散に対しては標本分散（不偏分散ではなく）になることがわかります。

モーメント法は、推定量の統計的性質（不偏性や有効性など）が最尤推定量に劣ることが多く、特に標本サイズが小さい場合にはその差が顕著になることがあります。

不偏分散って何だっけ？となった方はこちらで復習することをお勧めします

不偏性と不偏分散についてわかりやすく解説

【聞き流しデータサイエンス】不偏性についてわかりやすく解説