【生存時間解析】ワイブル分布をわかりやすく|確率分布とパラメータ推定方法
ワイブル分布は、製品の故障時間や材料の寿命、医療分野の生存時間解析などで広く使われている連続確率分布です。機械部品の寿命データや、生体における生存時間データを扱う際に非常に有用で、信頼性工学や生存分析の分野で欠かせない存在となっています。

また、形状パラメータを調整することで指数分布やレイリー分布などを近似できるため、柔軟性の高さが特徴です。
1. ワイブル分布の概要
1-1. ワイブル分布は「最弱リンクモデル」から誕生
ワイブル分布の背景には、「全体の強度や寿命は最も弱い箇所によって決定される」という最弱リンクモデルの考え方があります。鎖であれば最も弱い輪が切れた時点で鎖全体が破断し、製品であれば最も早く故障した部品が全体の寿命を左右するといったイメージです。
形状パラメータ ${k}$(または ${m}$)とスケールパラメータ ${\lambda}$(または ${\eta}$)の2つのパラメータを用いることで、初期不良が多い現象(${k < 1}$)から、時間が経つほど故障率が上がる摩耗故障現象(${k > 1}$)まで、さまざまなパターンを表現できます。
1-2. ワイブル分布の確率密度関数と分布関数
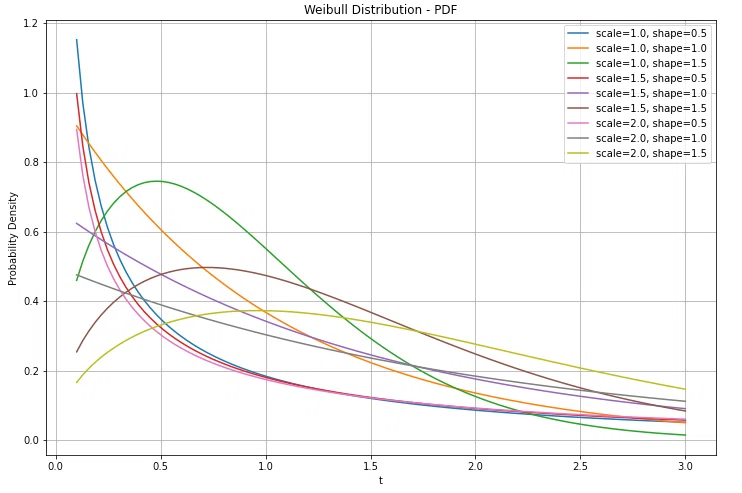
ワイブル分布の確率密度関数(PDF)は、以下のとおりです(${x \geq 0}$)
$${f(x; k, \lambda) \;=\; \frac{k}{\lambda} \Bigl(\frac{x}{\lambda}\Bigr)^{\,k-1} \exp\Bigl[-\bigl(\tfrac{x}{\lambda}\bigr)^{k}\Bigr]}$$
- ${k > 0}$ は形状パラメータ(shape parameter)
- ${\lambda > 0}$ はスケールパラメータ(scale parameter)
一方、累積分布関数(CDF)は、
$${F(x) \;=\; 1 \;-\; \exp\Bigl[-\bigl(\tfrac{x}{\lambda}\bigr)^{k}\Bigr]}$$
となります。
この ${F(x)}$は「ある時点 ${x}$ までに故障(もしくは事象が発生)している確率」を意味します。
2. 形状パラメータとスケールパラメータの意味
2-1. 形状パラメータ ${k}$
- ${k < 1}$:分布が左に裾を引き、初期不良が目立つ傾向を示唆
- ${k = 1}$:指数分布と同じ形状になり、故障率が一定(経時劣化や初期不良があまり影響しない)
- ${k > 1}$:分布が右に裾を引き、時間の経過とともに故障率が増加する“摩耗故障型”
つまり、製品やシステムがどのような故障パターンを持つかを大まかに推察できるのが形状パラメータです。
2-2. スケールパラメータ ${\lambda}$
スケールパラメータ ${\lambda}$ は、分布の広がりを決定づける指標です。値が大きいほど寿命や故障時間が長めの領域に分布が広がることを意味します。
寿命データ解析で用いられる場合、${\lambda}$ は「製品や生物個体における特性寿命」とも呼ばれ、約63.2%の個体・部品がそれまでに故障するとも解釈されます。
これは
$${F(\lambda) = 1 – e^{-1} \approx 0.632}$$
となることに対応します。
上記のようなパラメータを操作しながらワイブル分布の動きを見る場合、青の統計学-DS Playground-の確率分布可視化ツールが便利です。
以下のリンクをクリックすると、ワイブル分布の描画ページに飛びます。
3. 危険率(ハザード関数)と生存関数
ワイブル分布は、生存時間解析の文脈でもよく登場します。生存関数 ${S(t)}$ は「まだ故障していない(生存している)確率」であり、累積分布関数との関係は
$${S(t) = 1 – F(t) = \exp\Bigl[-\Bigl(\tfrac{t}{\lambda}\Bigr)^{k}\Bigr]}$$
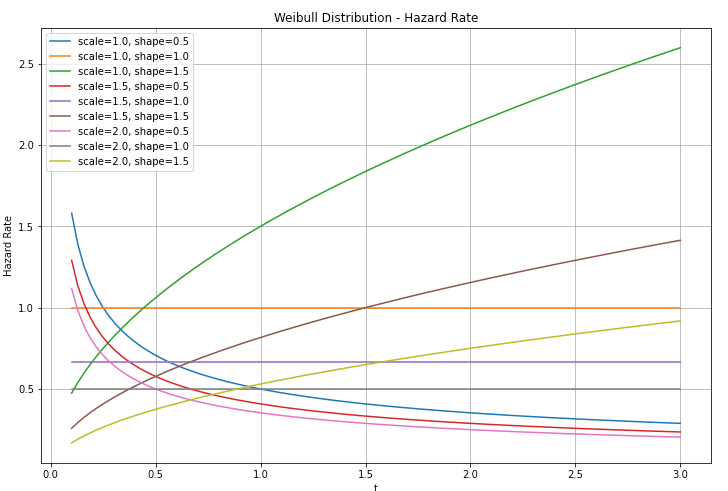
一方、危険率(ハザード関数)${h(t)}$ は、
$${h(t) = \frac{f(t)}{S(t)} = \frac{\tfrac{k}{\lambda}\,\Bigl(\tfrac{t}{\lambda}\Bigr)^{k-1} \exp\Bigl[-\bigl(\tfrac{t}{\lambda}\bigr)^k\Bigr]} {\exp\Bigl[-\bigl(\tfrac{t}{\lambda}\bigr)^k\Bigr]} = \frac{k}{\lambda}\,\Bigl(\tfrac{t}{\lambda}\Bigr)^{k-1}}$$
${k}$の値によって、危険率が時間とともに上昇・下降・一定になる様子を把握できるわけです。
4. ワイブル分布の指数分布との関係
前述のように、形状パラメータ ${k = 1}$ のとき、ワイブル分布は指数分布に一致します。指数分布は故障率(ハザード)が一定であるという特性を持つため、もし実際のデータが時間の経過に左右されない「偶発故障型」だと推定されるなら、ワイブル分布の特別なケースとして指数分布を使うことができます。
しかし、多くの機器・製品は経年劣化などを起こすため、常に故障率が一定とは限らないのが現実です。
その点、形状パラメータを自由に設定できるワイブル分布は、幅広い故障パターンを表現しやすい分布として重宝されています。
5. ワイブル分布のパラメータ推定方法
実際にワイブル分布を適用したい場合、観測データ(故障時間や寿命時間) から kkk と λ\lambdaλ を推定します。代表的な方法は以下のとおりです。
- 最尤推定法(MLE)
尤度関数を最大化するパラメータを探索する方法。- ${ \ell(k, \lambda) = \sum_{i=1}^n \ln f(x_i; k, \lambda)}$数値計算的に解くのが一般的です。
- 確率紙プロットによる推定
ワイブル分布専用の確率紙(Weibull probability paper)にデータをプロットし、近似的に直線を引くことでパラメータを読取る手法。直感的に分布への当てはまりを視覚的に確認できます。 - モーメント法
標本平均や標本分散などのモーメントを用いて、理論モーメントと一致させる方法。ただし、寿命データの場合は最尤推定や確率紙法の方がよく用いられます。
6. 応用分野
6-1. 信頼性工学・品質管理での使用例と論文
製造業の故障解析:ボールベアリングや電子部品の寿命データをワイブル分布に当てはめ、形状パラメータから初期故障が多いのか、摩耗故障が多いのかを判断する。
“Weibull analysis of bearing fatigue failure data”
- Journal of Tribology, Transactions of the ASME, 1998, Vol. 120(3), pp. 579-584
- ベアリングの疲労故障データをワイブル分布を用いて解析し、形状パラメータと寿命の関係を調べています。
6-2. 医療・生命科学での使用例と論文
- 生存時間解析(Survival Analysis):患者の術後生存や病気の発症までの期間をモデル化し、ハザード関数の形状から病気の進行パターンを考察する。
“Survival analysis: A self-learning text”
- David G Kleinbaum, Mitchel Klein; Statistics in medical research. New York: Springer, 2012.
- 生存時間解析の基礎的な教科書で、医学研究におけるワイブル分布の適用例などが紹介されています。
7. ワイブル分布の利点と限界
主な利点
- 柔軟性
初期故障から摩耗故障まで、形状パラメータ ${k}$ に応じて多彩なパターンを表現可能。 - 少ないサンプルでも推定が可能
ある程度小規模な寿命データでも、最尤推定などを通じて妥当な推計が得られやすいとされる。
とはいえ、以下のような限界もあったりします。
- 複雑な故障メカニズムには不向き
複数の故障モードが並列・直列に絡むようなケースでは、単一のワイブル分布では表現が難しく、混合分布などのモデルが必要。 - 外れ値(異常値)に敏感
特にサンプルサイズが小さい場合、極端な観測値が推定結果に大きく影響する。 - 適切なパラメータ推定が難しい場合も
初期故障期間や打ち切りデータ(censored data)が多い場合、最尤推定法に工夫が必要になることがある。
8. まとめ:ワイブル分布を使いこなし、寿命データを正しく読み解く
ワイブル分布は、「寿命」や「故障時間」に関するデータ解析において、他の分布にはない柔軟性と分かりやすさを提供します。形状パラメータ kkk の値によって故障傾向を把握できるため、製品の信頼性設計や医療における予後予測など、多岐にわたる分野で活用されています。
- 初期故障が多いのか、摩耗故障が多いのか?
- 故障率は時間とともに一定か、それとも上昇・下降するのか?
- 指数分布では説明しきれない現象をどこまで表現できるか?
これらの疑問を解決する上で、ワイブル分布は欠かせない道具となるでしょう。一方で、複雑な故障モードをすべて単独のワイブル分布で表現するのは困難であり、実際には混合モデルや複数パラメータモデルなど、さらなる拡張が必要になる場合もあります。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!






