【図解あり】ヤコビアンをわかりやすく解説【統計検定】

はじめに

こんにちは、青の統計学です。

今回は、ヤコビアンをテーマに解説をします。これは、多変数関数の振る舞いを理解するためのツールであり、特に変数の変換や最適化問題においてその真価を発揮します。

最初はなかなか理解が難しいかもしれませんが、MCMC法等の変数変換が必要な統計解析手法では必ず出てくる行列式です。

最後までお読みいただけると嬉しいです。

関連コンテンツはこちらをご覧ください。

【線形代数】固有値や固有ベクトルは機械学習にどう使われているのか|主成分分析

【python】行列式や逆行列は機械学習でどう使われるのか|線形代数の活用方法

導入：変数の微分から多変数の微分を考える

ヤコビアンの解説から行ってもしんどいので、まず、1変数の微分を思い出してみましょう。

関数 $y = f(x)$ の微分 $f'(x)$ は、ある点における関数の変化の割合、つまり接線の傾きを表していました。

これは、その点での関数の局所的な動きを捉えるものでしたね。

つまり、微小な変化 $\Delta x$ に対して、$f(x + \Delta x) \approx f(x) + f'(x) \Delta x$ と線形近似できることを意味します。

例えば、$z = f(x, y)$ のような2変数関数を考えてみましょう。

この場合、関数の変化は$x$方向と$y$方向の両方に依存します。そのため、単一の傾きでは関数の動きを完全に捉えることはできません。ここで登場するのが、偏微分ですね。

偏微分は、他の変数を固定して、ある特定の変数に対する変化の割合を調べますよね。しかし、これだけではまだ不十分です。関数の全体的な局所的な動きを捉えるためには、これらの偏微分をまとめて扱う必要があります。

導入｜なぜ行列として扱う必要があるのか

さて、導入が続きます。。。

多変数関数が複数の出力を持つ場合、例えば $y_1 = f_1(x_1, x_2)$ と $y_2 = f_2(x_1, x_2)$ のように、入力変数の変化が複数の出力変数にどのように影響するかを同時に考える必要があります。

このような状況では、各出力変数と各入力変数の間の偏微分をすべて考慮に入れる必要があり、これらを整理して表現するのに適した数学的構造が行列です。つまり、ヤコビアンは、多変数関数の局所的な線形変換を表現する行列として機能します。

具体的には、\(n\)次元のベクトル値関数\(f(X)\) に対して、そのヤコビ行列（またはヤコビアン行列）は、各成分の偏微分の行列として定義されます。

これは、ベクトル関数の変数の微小変化が出力にどのように影響するかを示しています。

数学的には、\( \mathbf{f}: \mathbb{R}^n \rightarrow \mathbb{R}^m \)のヤコビ行列は以下のように表されます。

\begin{equation}
J_{\mathbf{f}}(\mathbf{x}) =
\begin{bmatrix}
\frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\
\vdots & \ddots & \vdots \\
\frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n}
\end{bmatrix}
\end{equation}

数学的背景：線形近似としてのヤコビ行列

ヤコビアンを理解するために、その数学的な定義と幾何学的な意味を見ていきましょう。

多変数関数の微分可能性と全微分

1変数関数と同様に、多変数関数も微分可能性という概念を持ちます。関数 $f: \mathbb{R}^n \to \mathbb{R}^m$ がある点 $a$ で微分可能であるとは、その点で関数が局所的に線形関数で近似できることを意味します。この線形近似を表すのが全微分です。1変数関数の場合、全微分は $df = f'(x) dx$ でしたが、多変数関数の場合は、各入力変数の微小な変化が各出力変数に与える影響をすべて考慮する必要があります。

ヤコビ行列の定義：偏微分の並び

$n$個の入力変数 $x = (x_1, x_2, \dots, x_n)$ と $m$個の出力変数 $y = (y_1, y_2, \dots, y_m)$ を持つベクトル値関数 $y = f(x)$ を考えます。

ここで、$y_i = f_i(x_1, x_2, \dots, x_n)$ となります。

このとき、ヤコビ行列 $J$ は、$m \times n$ 行列として次のように定義されます。

$$ J = \frac{\partial(y_1, \dots, y_m)}{\partial(x_1, \dots, x_n)} = \begin{pmatrix}\frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \cdots & \frac{\partial y_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \frac{\partial y_m}{\partial x_2} & \cdots & \frac{\partial y_m}{\partial x_n}\end{pmatrix} $$

接平面（超平面）と線形写像としての解釈

ヤコビ行列は、関数が与えられた点において、その関数を最もよく近似する線形変換（線形写像）を表します。例えば、2変数関数 $z = f(x, y)$ の場合、ヤコビ行列は1行2列のベクトルとなり、その点における接平面の傾きを決定します。

つまり、ヤコビ行列は、多変数関数のグラフの接平面や接超平面の概念を一般化したものと捉えることができます。

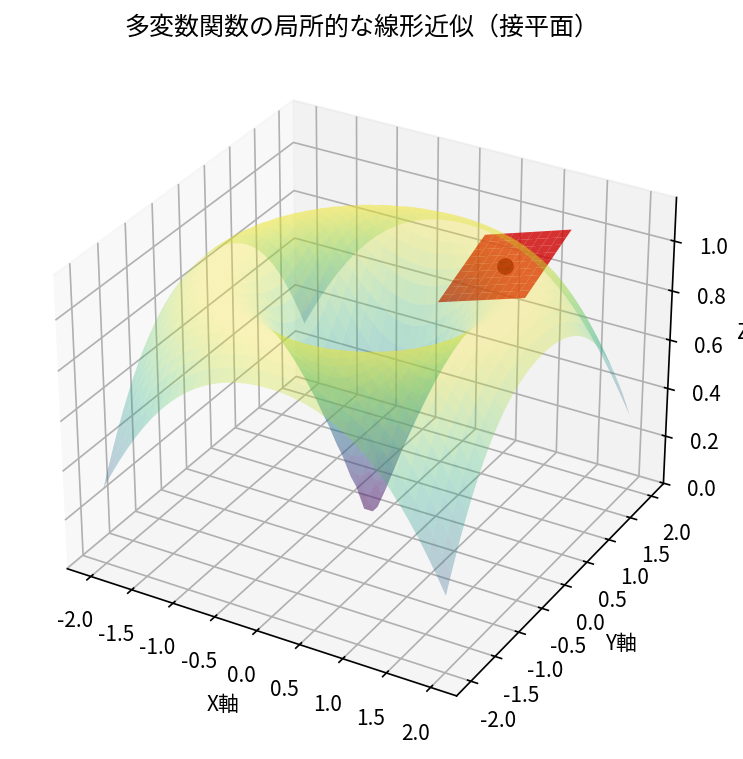
この図は、3次元空間における曲面（多変数関数）と、その一点における接平面を示しています。ヤコビ行列は、この接平面の傾きを決定し、関数がその点でどのように振る舞うかを線形的に近似する役割を担っています。

面積・体積の拡大率：ヤコビ行列式の幾何学的意味

ヤコビ行列が関数の局所的な線形近似を表すのに対し、その行列式であるヤコビ行列式は、変数の変換によって微小な領域（面積や体積）がどれだけ拡大・縮小されるか、その拡大率を教えてくれます。

行列式が表すもの（平行四辺形の面積）

線形代数で学んだように、2次元の正方行列 $A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ の行列式 $det(A) = ad – bc$ は、基底ベクトル $(1, 0)$ と $(0, 1)$ が線形変換 $A$ によって移されたベクトルが張る平行四辺形の面積を表します。3次元であれば、平行六面体の体積を表します。

微小領域 $du dv$ が $dx dy$ に移る際の歪み

2つの変数 $u, v$ から2つの変数 $x, y$ への変換 $x = x(u, v)$, $y = y(u, v)$ を考えましょう。このとき、$(u, v)$ 平面上の微小な長方形領域 $du dv$ が、$(x, y)$ 平面上でどのような領域に変換されるかを考えます。この微小長方形は、変換によって一般的には平行四辺形に歪みます。この歪んだ平行四辺形の面積は、元の長方形の面積 $du dv$ にヤコビ行列式の絶対値を掛けたものに等しくなります。

$$ dx dy = \left| \det \left( \frac{\partial(x, y)}{\partial(u, v)} \right) \right| du dv = \left| \begin{vmatrix}\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v}\end{vmatrix} \right| du dv $$

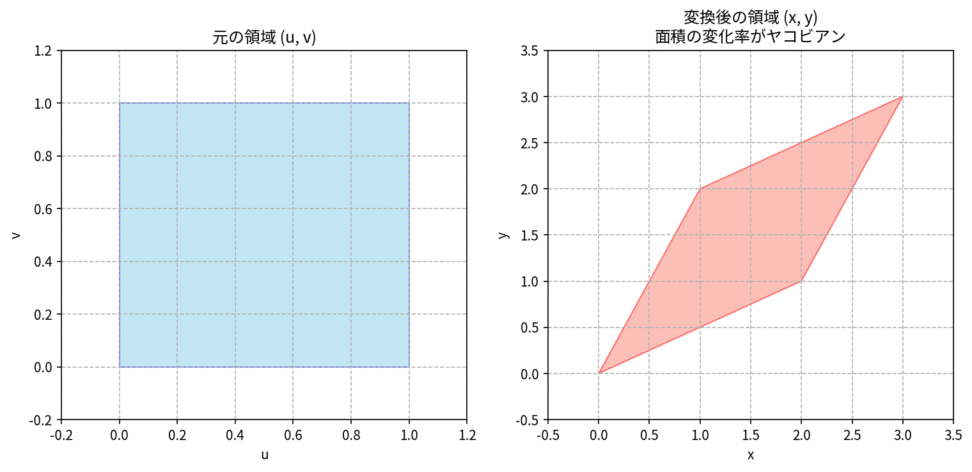
この図は、$(u, v)$ 空間の小さな正方形が、ある変換によって $(x, y)$ 空間で平行四辺形に変換される様子を示しています。ヤコビ行列式は、この変換によって面積がどれだけ変化するか（拡大または縮小されるか）の比率を与えます。

ヤコビアンの使い道

多重積分における置換積分

ヤコビアンが使える場面の一つが、多重積分における置換積分です。1変数関数の置換積分では、変数を変換する際に $dx = g'(u) du$ のように $g'(u)$ を掛けて補正しました。

多変数関数の場合も同様に、変数を変換する際にヤコビ行列式で補正を行います。

積分変数の変換公式

領域 $D$ 上での $n$ 変数関数 $f(x_1, \dots, x_n)$ の積分を、新しい変数 $u_1, \dots, u_n$ を用いて計算したい場合、次のような変換公式が成り立ちます。

$$ \int \cdots \int_D f(x_1, \dots, x_n) dx_1 \cdots dx_n = \int \cdots \int_{D’} f(x_1(u), \dots, x_n(u)) \left| \det \left( \frac{\partial(x_1, \dots, x_n)}{\partial(u_1, \dots, u_n)} \right) \right| du_1 \cdots du_n $$

• $D’$ ：変換後の新しい領域
• $\left| \det \left( \frac{\partial(x_1, \dots, x_n)}{\partial(u_1, \dots, u_n)} \right) \right|$ ：ヤコビ行列式の絶対値
  • この項が、変数変換によって生じる微小体積要素の拡大・縮小を補正する役割を担っています。積分計算において測度を正しく変換するための重みとして機能する。

極座標変換を例にした具体的な計算

最もよく知られた例の一つが、デカルト座標 $(x, y)$ から極座標 $(r, \theta)$ への変換です。変換式は次のようになります。

$x = r \cos \theta$

$y = r \sin \theta$

このときのヤコビ行列を計算してみましょう。

$$ J = \begin{pmatrix}\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta}\end{pmatrix} = \begin{pmatrix}\cos \theta & -r \sin \theta \\ \sin \theta & r \cos \theta \end{pmatrix} $$

そして、ヤコビ行列式は

$$ \det(J) = (\cos \theta)(r \cos \theta) – (-r \sin \theta)(\sin \theta) = r \cos^2 \theta + r \sin^2 \theta = r(\cos^2 \theta + \sin^2 \theta) = r $$

したがって、極座標変換におけるヤコビ行列式の絶対値は $|r|$ となります。通常、$r \ge 0$ なので $r$ です。この結果から、$dx dy = r dr d\theta$ となることがわかります。これは、極座標での微小面積要素が $r dr d\theta$ となることを意味しており、ヤコビアンがこの幾何学的な事実を数学的に裏付けていることがわかりますね。

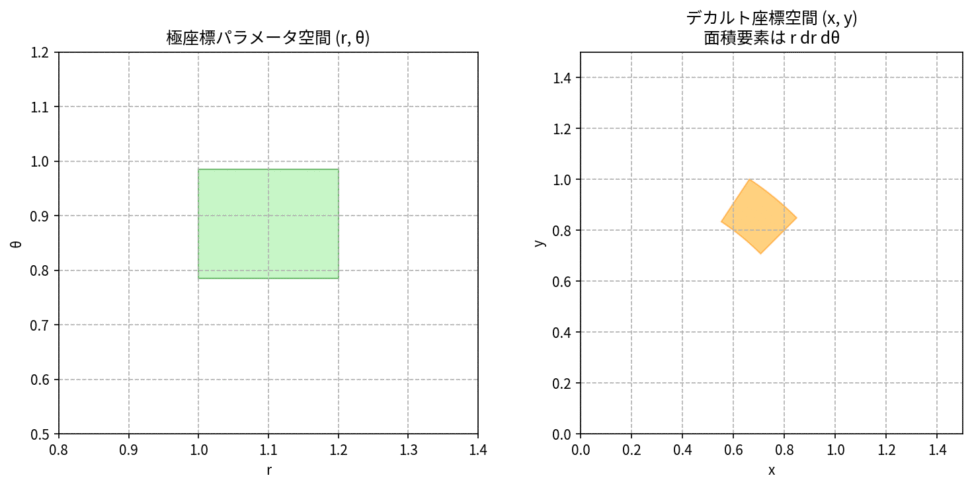
この図は、極座標パラメータ空間の微小な長方形領域が、デカルト座標空間で扇形のような領域に変換される様子を示しています。この変換によって生じる面積の変化率が、ヤコビ行列式 $r$ によって正確に捉えられていることが視覚的に理解できます。

確率密度関数の変数変換

ちょっと冒頭の方でも解説したのですが、ヤコビアンは確率密度関数の変数変換に不可欠な役割を果たします。

さて、ある確率変数 $X$ の確率密度関数 $f_X(x)$ が与えられているとき、別の確率変数 $Y = g(X)$ の確率密度関数 $f_Y(y)$ を求めたい、という状況は頻繁に発生します。このとき、ヤコビアンが確率の保存を保証するための補正項として登場します。

$Y = g(X)$ のときの密度関数の変化

1変数の場合を考えてみましょう。確率変数 $X$ の確率密度関数が $f_X(x)$ で与えられ、単調な関数 $Y = g(X)$ によって $Y$ が定義されるとします。このとき、$Y$ の確率密度関数 $f_Y(y)$ は次のように与えられます。

$$ f_Y(y) = f_X(g^{-1}(y)) \left| \frac{d}{dy} g^{-1}(y) \right| = f_X(g^{-1}(y)) \left| \frac{dx}{dy} \right| $$

ここで、$\left| \frac{dx}{dy} \right|$ は、まさに1変数のヤコビ行列式（導関数の絶対値）です。

これは、変数変換によって確率の「密度」がどのように変化するかを調整する役割を担っています。つまり、微小な確率 $P(x \le X \le x + dx) = f_X(x) dx$ が、変換後も $P(y \le Y \le y + dy) = f_Y(y) dy$ として等しくなるように、ヤコビアンが調整しているのです。

多変数の場合も同様です。確率ベクトル $X = (X_1, \dots, X_n)$ の同時確率密度関数が $f_X(x_1, \dots, x_n)$ で与えられ、可逆な変換 $Y = g(X)$ によって確率ベクトル $Y = (Y_1, \dots, Y_n)$ が定義されるとします。このとき、$Y$ の同時確率密度関数 $f_Y(y_1, \dots, y_n)$ は次のように与えられます。

$$ f_Y(y_1, \dots, y_n) = f_X(g^{-1}(y_1, \dots, y_n)) \left| \det \left( \frac{\partial(x_1, \dots, x_n)}{\partial(y_1, \dots, y_n)} \right) \right| $$

ここでのヤコビ行列式は、逆変換 $X = g^{-1}(Y)$ のヤコビ行列式です。

正規分布の導出や、多変量正規分布への拡張

この変数変換の公式は、統計学の多くの場面で利用されます。

例えば、標準正規分布から一般の正規分布を導出する際や、ベータ分布やガンマ分布といった様々な分布の性質を調べる際に用いられます。また、複数の確率変数を同時に扱う多変量正規分布の理論においても、変数変換とヤコビアンの概念は関わってきます。独立な標準正規分布に従う複数の確率変数から、相関を持つ多変量正規分布を生成する際など、ヤコビアンがその変換の歪みを適切に補正する役割を担います。

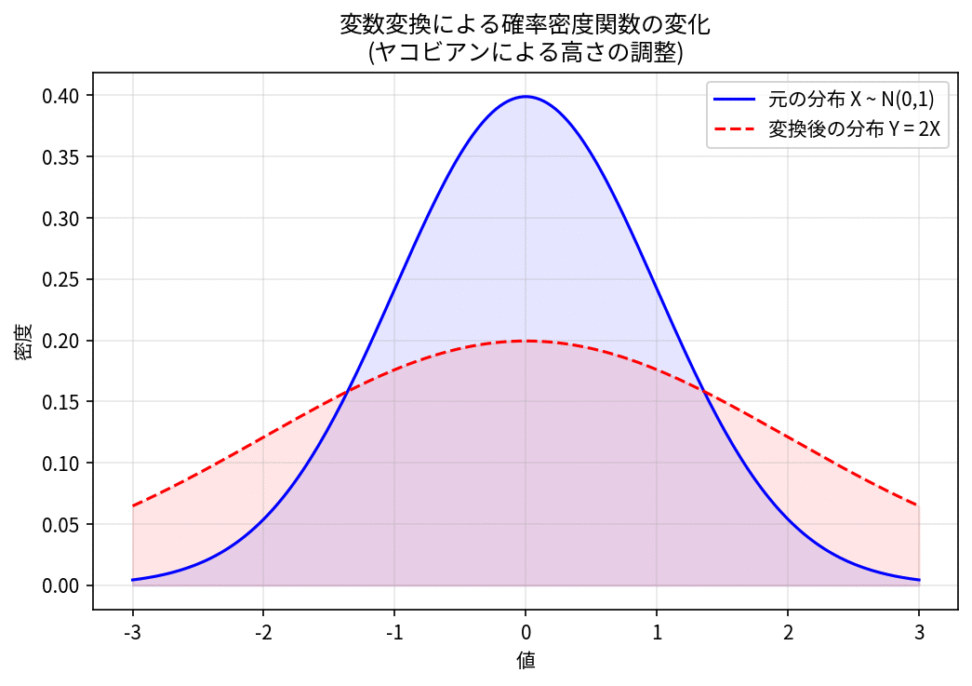
この図は、確率密度関数が変数変換によってどのように変化するかを示しています。元の分布（青）が、ある変換によって別の分布（赤）に変わっています。ヤコビアンは、この変換によって確率の「密度」が薄まったり濃くなったりする度合いを調整し、確率の総和が常に1に保たれるように補正します。

MCMC法とヤコビアン

MCMCは確率分布からのサンプリングに使用される一連のアルゴリズムです。

MCMC法については、以下のコンテンツで詳しく解説しております。

【完全ガイド】MCMC法についてわかりやすく解説|ベイズ推定

MCMCでは、複雑な事後分布から直接サンプリングすることが難しいため、より単純な分布に変換してからサンプリングを行います。その後、ヤコビアンを用いて元の分布に戻します。

例えば、MCMCの一般的な手法であるメトロポリス・ヘイスティングスアルゴリズムでは、提案分布からサンプリングし、それを元の分布に変換する際にヤコビアンが必要になります。

以下のように、パラメータ\(\theta\)から\(\theta’\)への移動を考えてみます。

この移動、というか提案は提案分布\(q(\theta’|\theta)\)に基づいて行われます。

新しい状態\(\theta’\)は、ある受容確率\(α(\theta’|\theta)\)に基づいて、採択か棄却が決まります。

(上にご提示したMCMCについてのコンテンツでは、補正係数\(r\)としていますが、意味は同じです。)

この受容確率は以下のように定義されます

$$\alpha\left(\theta^{\prime} \mid \theta\right)=\min \left(1, \frac{P\left(\theta^{\prime}\right)q\left(\theta \mid \theta^{\prime}\right)}{P(\theta) q\left(\theta^{\prime} \mid \theta\right)}\right)$$

さて、変数(パラメータ)変換を行う場合、事後分布の形が変わるため、ヤコビアンを用いて調整する必要があります。

仮に、以下のような関係があったとします。

$$\theta=g(\theta’)$$

このとき、現在の事後分布\(P(\theta)\)は、\(\theta’\)の確率密度関数\(Q(\theta’)\)に変換されます。

ヤコビアン\(\mathbf{J}\)を用いて、次のように表されます。

$$Q(\theta’)=P(g(\theta’))・|\mathbf{J}(\theta’)|$$

さて、もう一踏ん張りです(汗)

MCMCにおいて変数変換を行う場合、変換後の確率密度関数と変換前の確率密度関数の間にはヤコビアンを通して関連があります。

$$Q(\theta’)=P\left(g^{-1}(\theta’)\right) \cdot\left|J_{g^{-1}}(\theta’)\right|$$

逆関数を使っています。

ここで、

\(g^{-1}\)は\(\theta’\)から\(\theta\)への逆変換関数です。

\(|J_{g^{-1}}(\theta’)|\)がこの逆変換関数のヤコビ行列の行列式、つまりヤコビアンです。

他の変数変換については、こちらのコンテンツがおすすめです。