【外れ値に対処】順位相関係数と相関係数の違いについて | python
相関係数は、外れ値があると大きく値が変わってしまうという特徴があり、正確な関係の把握が難しい場合があります。
そこで、外れ値に対処できる頑健(ロバスト)な相関係数が必要とされます。
それが、スピアマンの順位相関係数と呼ばれるものです。
今回は、順位相関係数の理論と実装を扱います。
末尾に、相関係数をpythonで実装しているので興味がある方はご覧ください。
順位相関係数
相関係数の理解が怪しい方は、下の「おまけ:相関係数の実装」からみてください。
今回は与えられたデータを並べ替えることで、検定統計量を作ります。
背景となる分布を仮定しないことから、ノンパラメトリックな推定と呼ばれています。
順位相関の他にも、ウィルコクソンの順位和検定などが仲間に入ります。
順位相関係数は、その名の通りデータの大きさ順に並べる必要があります。
まず、数式を見てみましょう。
$$ρ=1-{\frac{6\sum(d_{i})^2}{n(n^2-1)}}$$
この\(d_i\)というのは、各観測値の2つの順位の差です。
例えば、\((x_{1},y_{1})\)のデータを考えてみましょう。
x1:xの中では3番目に小さい。
y1:yの中では9番目に小さい。
このことから\(d_{1}=6\)になります。
順位は、「ランク」と呼んだりします。
順位の差を二乗し、和を取ったものに6をかけたものが分子になっており、1から引いているので、
順位の差が大きいほど、順位相関係数は小さくなります。
順位相関係数は、その特性から2変数のデータの順序が全て一致する場合は1を取り、逆順にすると全て一致する時は-1を取ります。
どんな場面で使うかというと、「データが順位尺度のとき」です。
例えば、学校のテストの順位です。周りの学生に比べて、非常に高い点数や、低い点数を取った学生のデータは、外れ値です。
普通に相関係数を求めるとき、この「外れ値」に相関係数の値が引っ張られます。
データのかたまりの中心から水平に離れている点は直線をよりひどく引っ張る傾向にあるので, こうした点をを高レバレッジ (high leverage) 点と呼んだりします
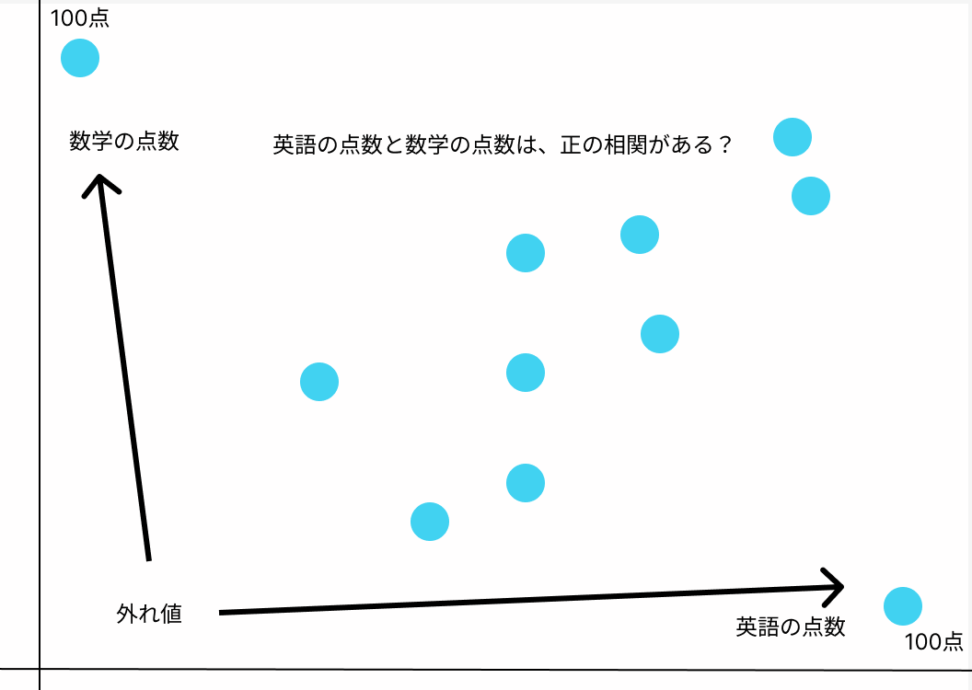
では、実際に具体例を通してpythonで順位相関係数を実装してみましょう。
CODE
先ほどの例を使ってみましょう。
試しに、「英語が大得意だけど、数学は珍紛漢紛」、「数学は毎回9割とるけど、英語は壊滅的」な外れ値的2人を用意します。
| 生徒id | English | Math |
| 1 | 1 | 9 |
| 2 | 9 | 10 |
| 3 | 2 | 3 |
| 4 | 5 | 5 |
| 5 | 3 | 4 |
| 6 | 6 | 7 |
| 7 | 10 | 1 |
| 8 | 4 | 2 |
| 9 | 7 | 8 |
| 10 | 8 | 6 |
import numpy as np
ma = [1, 9, 2, 5, 3, 6, 10, 4, 7, 8]
en = [9, 10, 3, 5, 4, 7, 1, 2, 8, 6]
def spearman(subject1, subject2):
sub1Order = np.array(subject1)
sub2Order = np.array(subject2)
N = len(subject1)
return 1 - (6*sum((sub1Order -sub2Order)**2) / (N*(N**2 - 1)))
spearman(ma ,en)このように順位相関係数を求める関数を作ってみました。
引数に、今回扱うリスト型のデータを入れておしまいです。
順位相関係数は、0.042でした。
おまけ:相関係数の実装
ここでは、関数で簡単に求められる相関係数を1からpythonで実装してみようと思います。
相関係数については、【高校生向け】データの活用の例題①(Lv共通テスト)や【高校生向け】データの活用の例題②(Lv共通テスト)で詳しく解説しております。
高校生向けの記事なので平易に書かれております。
ご存じのとおり、相関係数は2つの確率変数間の間にある線形関係の強弱を示す指標ですね。
相関係数は、無次元量であり、-1から1の実数値を取ります。
$$r={\frac{Cov(X,Y)}{{\sqrt{Var(X)}}{\sqrt{Var(Y)}}}}$$
上のように、2つの確率関数の共分散をそれぞれの標準偏差の積で割ると相関係数がでます。
ここで紹介している相関係数は、ピアソンの積率相関係数と呼ばれ、共分散を-1から1の範囲で正規化したものだとわかります。
#ライブラリのインポート
import random
import numpy as np
import matplotlib.pyplot as plt
#乱数の調整
random.seed(0)今回は乱数を使って相関係数を出します。
#xy共に50個の乱数を発生させる
x = np.random.randn(50)
y = np.sin(x)+np.random.randn(50)
#グラフの大きさを設定
plt.figure(figsize=(16,6))
#作図
plt.plot(x,y,"o")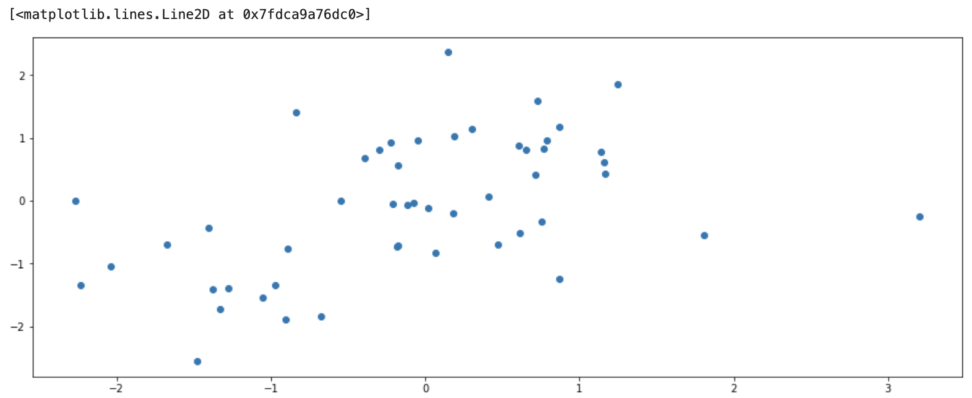
#相関係数を求める関数を作ります
def correlation(data1,data2):
#平均
mean1 = sum(data1)/len(data1)
mean2 = sum(data2)/len(data2)
#標準偏差
deviation1 = math.sqrt(sum((data1-mean1)**2))
deviation2 = math.sqrt(sum((data2-mean2)**2))
#共分散
covariance = sum((data1-mean1)*(data2-mean2))
#戻り値
return covariance/(deviation1 * deviation2)
#相関係数
correlation(x,y)相関係数求める関数correlationを作りました。
サンプル数で割ってないと思われるかもしれませんが、2つの確率変数の値が同じ場合なら分母と分子で打ち消し合うので1/nを掛けなくてもokです。
出力結果は、0.537902‥になりました。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!


