【統計検定準一級】回帰診断法とは?|残差プロットとleverageをわかりやすく解説
回帰診断法
回帰診断法は、回帰分析において誤差項の仮定が成立しているかどうかを評価する手法です。
- 独立性: 誤差項は互いに独立である
- 等分散性: 誤差項の分散が一定であること(等分散性)
- 正規性: 誤差項が正規分布に従うこと
仮定について詳しく深掘りたい方は、こちらを先に見た方がいいかもしれないです
…で、これらの仮定を確認するために、以下のようなプロットを用います。
- 残差プロット: 予測値に対する残差をプロットし、残差が0を中心にランダムに分布しているかを確認します。これにより、モデルの線形性や外れ値の影響を評価できます。
- 正規Q-Qプロット: 残差の分位点と標準正規分布の分位点を比較し、残差が正規分布に従っているかを判断します。直線上に並ぶ場合、正規性が成立していると考えられます。
- 標準化残差の平方根プロット: 予測値に対する標準化した残差の絶対値をプロットし、等分散性が成立しているかを確認します。傾向が見られる場合は、等分散性が疑われます。
- 梃子比(Leverage)プロット: 各観測データが回帰係数に与える影響度を示します。Cook距離と呼ばれる指標も用いられ、特定のデータポイントがモデルに与える影響を評価します。Cook距離が0.5を超えると、そのデータは外れ値である可能性があります
代表的な、残差プロットとLeverageについて紹介していきます。
残差プロット
まず、残差の定義から確認しましょう。
残差 $e_i$ は、観測値 $y_i$ と予測値 $\hat{y}_i$ の差として定義されます。
$$ e_i = y_i – \hat{y}_i $$
残差は0を中心としてランダムに散らばる必要があります。
通常、x軸に予測値 $\hat{y}_i$ または独立変数 $x_i$、y軸に残差 $e_i$ をプロットします。
理想的な残差プロットでは、残差はランダムに分布し、特定のパターンを示さないはずです。
分解すると以下のような要素で理想的な残差プロットに近づきます。
- 残差の平均が0に近い
- 残差の分散が一定(等分散性)
- 残差が正規分布に従う
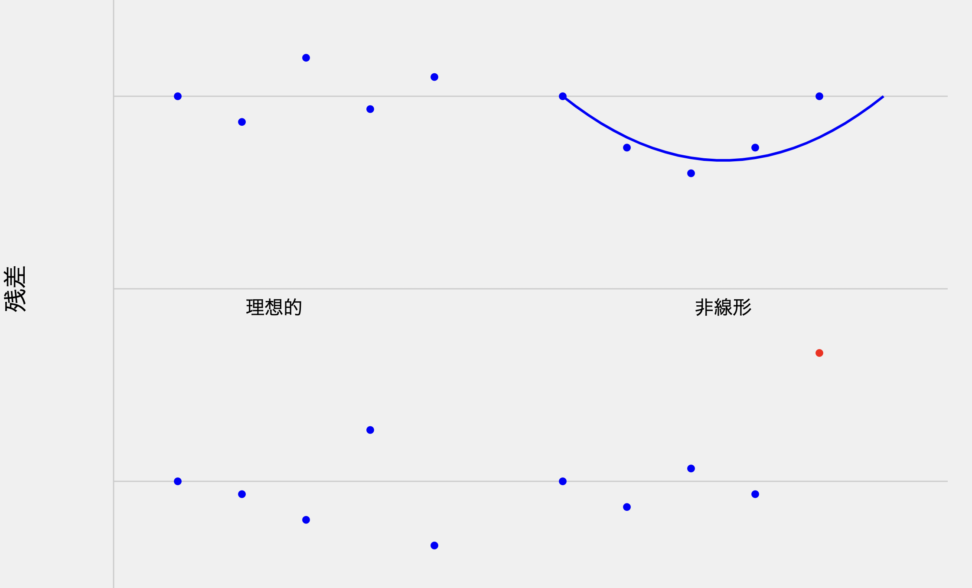
理想的(左上): 残差が0を中心にランダムに散らばっています。これはイイ感じです。
非線形(右上): 残差が曲線を描いています。これは、モデルに非線形性が存在することを示唆し、非線形項の追加が必要かもしれません。
不等分散(左下): 残差の散らばりが予測値とともに増加しています。不等分散性が示唆されます。変数変換や重み付き最小二乗法が必要かもしれません。
外れ値(右下): 他の点から大きく離れた点(赤で表示)が存在します。影響力の大きな観測値や潜在的な誤差が示唆されますね。
また上記以外にでも、残差に明確なパターンがある場合、時系列データにおける自己相関の存在が示唆されます。
Leverage(てこ比)
てこ比の理解には、ハット行列(射影行列)の理解が必須です。
端的にいうと、ハット行列 $\mathbf{H}$ の対角成分なのですが、こいつが大きいと回帰係数への影響が大きいことから,外れ値の候補になります。
ハット行列の導出までお付き合いください。
まず、線形回帰モデルを行列形式で表現します
$$ \mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\epsilon} $$
- $\mathbf{y}$ は $n \times 1$ の応答変数ベクトル
- $\mathbf{X}$ は $n \times (p+1)$ のデザイン行列(切片項を含む)
- $\boldsymbol{\beta}$ は $(p+1) \times 1$ の回帰係数ベクトル
- $\boldsymbol{\epsilon}$ は $n \times 1$ の誤差項ベクトル
さて、OLS推定量を出してみます。
最小二乗法による $\boldsymbol{\beta}$ の推定量 $\hat{\boldsymbol{\beta}}$ は
$$ \hat{\boldsymbol{\beta}} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y} $$
予測値 $\hat{\mathbf{y}}$ は
$$ \hat{\mathbf{y}} = \mathbf{X}\hat{\boldsymbol{\beta}} = \mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y} $$
ハット行列 $\mathbf{H}$ は以下のように定義されます
$$ \mathbf{H} = \mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T $$
ハット行列は以下の性質を持ちます。
- 対称行列:$\mathbf{H}^T = \mathbf{H}$
- べき等行列:$\mathbf{H}^2 = \mathbf{H}$
- トレースは $(p+1)$:$\text{tr}(\mathbf{H}) = p+1$
Leverageの数学的表現
Leverage(てこ比)は、ハット行列 $\mathbf{H}$ の対角要素として定義されます。
$$ h_{ii} = \mathbf{x}_i^T(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{x}_i $$
$\mathbf{x}_i^T$ は $\mathbf{X}$ の $i$ 行目を表します。
- $0 \leq h_{ii} \leq 1$
- $\sum_{i=1}^n h_{ii} = p+1$
- 平均的なLeverageは $(p+1)/n$
肝心の解釈についてですが、高いLeverage値(一般的に $h_{ii} > 2(p+1)/n$ または $h_{ii} > 3(p+1)/n$)は、その観測値が他の観測値から離れていることを示唆します。
Leverage値が高い観測値は、回帰モデルの係数推定に大きな影響を与える(=観測点 ${i}$ が他のデータに比べて極端に大きな影響を持っているかどうかを判断できる)可能性があります。
データがモデルにどれだけ適合しているか、なので残差(観測値と予測値の差)がどれだけ縮小されたかを知る助けになります。予測値が観測値に非常に近い場合は、てこ比は小さくなりますよね。
cook距離との関係
Cook距離は、サイズnの全サンプルから特定のデータを除いて推定したときに回帰係数が大きく変化するのかを調べるもので
Cook距離 $D_i$ は以下の式で表されます。
$$ D_i = \frac{r_i^2}{p} \cdot \frac{h_{ii}}{(1-h_{ii})^2} $$
$r_i$ は標準化残差、$p$ は説明変数の数、$h_{ii}$ はLeverageです。
式を見ていただいたらわかるとおり、Cook距離はLeverageと標準化残差の両方に影響されます。
なので、高いLeverageまたは高い残差のどちらかだけでは、必ずしも高いCook距離にはなりません。
解釈としては、Cook距離が高い点は、回帰モデルの係数推定に大きな影響を与える可能性があります。Cook の距離が 0.5 を超えると影響が大きいとされ、1 を超えるとモデルに極端な影響を与える可能性があるデータ点として注目すべきですね。
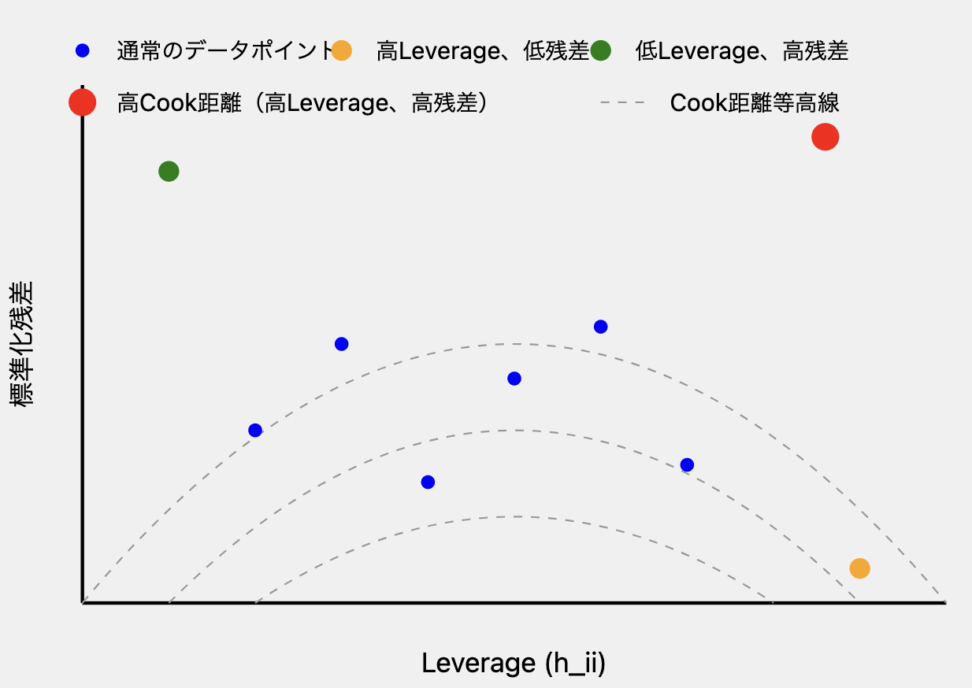
- 青い点:通常のデータポイント
- オレンジの点:高Leverage、低残差のポイント。Cook距離は中程度です。
- 緑の点:低Leverage、高残差のポイント Cook距離は中程度。
- 赤い点:高Leverage、高残差のポイント。高いLeverageと高い残差を持ち、結果として高いCook距離を示します。
- 破線の曲線:Cook距離等高線 これらの線は同じCook距離値を持つ点を結んでいます。原点から遠いほどCook距離が高くなります。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!




