【例題付き】ラグランジュ未定乗数法の基本と応用をわかりやすく解説
ラグランジュの未定乗数法の基礎
ラグランジュの未定乗数法は、条件付き（制約付きともいう）最適化問題を解決するための数学的手法です。
条件付き最適化問題とは？
ラグランジュ法を使うと、「ある制約条件を満たしながら、一番いい選択肢を探す」ということができます。
例えば、次のような問題があるとしましょう
例題：「${x}$と${y}$の合計が${10}$になるようにしながら、${xy}$の値を最大にしたい。」
ここでの目的は「${xy}$を最大にする」ことで、制約条件は「${x+y=10}$」です。
もしも制約条件（つまり「${x+y=10}$」）がなかったとしましょう。この場合、単に${xy}$をどんどん大きくするためには、${x}$や${y}$を限りなく大きくすれば良いですね。でも今回は、「${x+y=10}$」という条件を守らないといけません。
さて、ラグランジュの未定乗数法は、このような制約条件の下で関数の極値を求めるための手法です。
未定乗数法は、制約条件を考慮しながら、関数の極値を求めるために、新たな変数（未定乗数）を導入します。この未定乗数は、制約条件を満たすように調整されます。
数学的な背景
ラグランジュの未定乗数法は、微分積分学と線形代数の概念に基づいています。
特に、関数の極値を求めるための必要条件である、勾配ベクトルがゼロになるという条件を使います（高校でも使いますね）
制約条件は、関数の定義域を制限する等式または不等式の形で表されます。未定乗数は、これらの制約条件を満たすように調整されます。
では、数式を使ってみていきましょう。
多次元における未定乗数法
2次元のケース
2次元のケースでは、ラグランジュの未定乗数法は、2つの変数を持つ関数と1つの制約条件を扱う場合に適用されます。
例えば、${x}$と${y}$の関数${f(x,y)}$を、制約条件${g(x, y) = c}$の下で最大化することを考えます。
この場合、ラグランジュ関数${L(x, y, \lambda)}$は次のように定義されます。
$${L(x,y, \lambda) = f(x, y) + \lambda(g(x, y) – c) }$$
ここで、λは未定乗数です。
ラグランジュ関数の極値を求めるには、L(x, y,λ)の偏微分をゼロに設定し、x、y、λについて解きます。
具体的には、以下の3つの方程式を連立して解きます
${\frac{\partial L}{\partial x} = \frac{\partial f}{\partial x} + λ\frac{\partial g}{\partial x} = 0}$
${\frac{\partial L}{\partial y} = \frac{\partial f}{\partial y} + λ\frac{\partial g}{\partial y} = 0}$
${\frac{\partial L}{\partial λ} = g(x,y) – c = 0}$
これらの方程式を解くことで、以下の情報が得られます
- 制約条件を満たす候補点(${\hat{x}, \hat{y}}$)の座標
- その点でのラグランジュ乗数${\hat{\lambda}}$の値
ラグランジュ乗数の解釈
- ${\hat{\lambda}}$の値は、制約条件が少し変化したときの目的関数の変化率を表します。
- 例えば、${\hat{\lambda} = 2}$なら、制約条件の値${c}$を1単位増やしたとき、最適値は約2単位変化することを示唆します。
二次条件の確認
この解が得られた後は、二次条件を確認します(答えは出ているが念の為確認してほしい)
具体的には、ラグランジュ関数の二次偏導関数行列（ヘッセ行列）を評価し、極値の性質（極大値か極小値か）を判定します。
ちょっと難しいと思うので補足します。
まず基本的な考え方として、1変数の場合を思い出してください。
例えば${y = x^2}$のような関数で一回微分して${y’ = 0}$となる点を見つけると、それは極値の候補点です。（ここまでできた）
それを二回微分して${y” > 0}$なら極小値、${y” < 0}$なら極大値だと判断できます。
↑これはなぜか。具体例をみましょう。
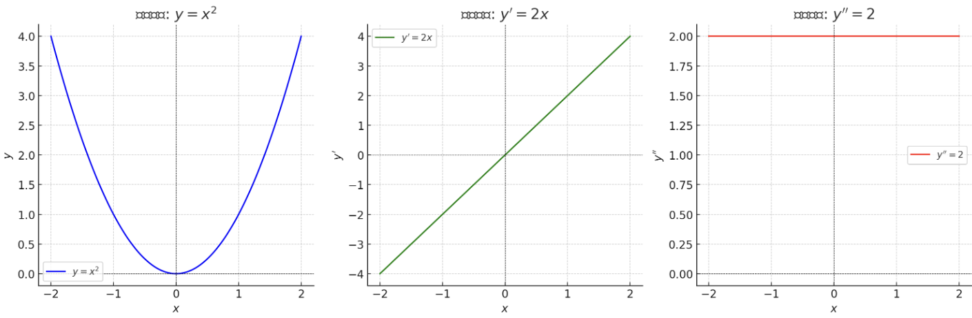
- 左のグラフ：元の関数 ${y = x^2}$
- 放物線の形をしています
- ${x = 0}$の点が最も低くなっています（極小値の候補点）
- 真ん中のグラフ：一回微分 ${y’ = 2x}$
- 直線ですね
- ${x = 0}$で${y’ = 0}$となります（これが極値の候補点です）
- 右のグラフ：二回微分 ${y” = 2}$
- 常に2という一定値になります
- ${y” > 0}$なので、${x = 0}$の点は極小値と判定できます
このように、二階導関数が正（${y” > 0}$）であることから、${x = 0}$での極値は極小値であることがわかります。
もし二階導関数が負（${y” < 0}$）だった場合は極大値となります。
ちなみに、2変数の場合は少し複雑になります
- 関数${f(x,y)}$の場合、極値の性質を調べるには、次の値を計算します：
- ${f_{xx}}$ : ${x}$で二回微分
- ${f_{yy}}$ : ${y}$で二回微分
- ${f_{xy}}$ : ${x}$で一回、${y}$で一回微分（${f_{yx}}$と同じ値になります）
ヘッセ行列
これらをまとめて行列にしたものが、ヘッセ行列です。
$${H = \begin{pmatrix} f_{xx} & f_{xy} \\ f_{xy} & f_{yy} \end{pmatrix}}$$
例えば${f(x,y) = x^2 + y^2}$の場合
- ${f_{xx} = 2}$
- ${f_{yy} = 2}$
- ${f_{xy} = 0}$
となり、ヘッセ行列は
$${H = \begin{pmatrix} 2 & 0 \\ 0 & 2 \end{pmatrix}}$$
となります。
判定方法
- ヘッセ行列が正定値（全ての固有値が正）なら、その点は極小値
- ヘッセ行列が負定値（全ての固有値が負）なら、その点は極大値
- どちらでもない場合は鞍点の可能性がある
一般的な多次元のケース
一般的な多次元のケースでは、ラグランジュの未定乗数法は、n個の変数を持つ関数とm個の制約条件を扱う場合に適用されます。
例えば、${n}$個の変数${x_1,x_2, …、x_n}$を持つ関数${f(x_1,x_2, …、x_n)}$を、${m}$個の制約条件${g1(x_1,x_2, …、x_n) = c1、g2(x_1,x_2, …、x_n) = c2、…、gm(x_1,x_2, …、x_n) = cm}$の下で最大化することを考えます。
この場合、ラグランジュ関数${L(x_1,x_2, …、x_n, \lambda_1、\lambda_2、…、\lambda_m)}$は次のように定義されます。
${L(x_1, x_2, …, x_n, \lambda_1, …, \lambda_m) = }$
${f(x_1, x_2, …, x_n) + \lambda_1(g_1(x_1, x_2, …, x_n) – c_1) +}$
${\lambda_2(g_2(x_1, x_2, …, x_n) – c_2) + … +}$
${\lambda_m(g_m(x_1, x_2, …, x_n) – c_m)}$
ここで、${\lambda_1、\lambda_2、…、\lambda_m}$は未定乗数です。
ごちゃごちゃしていますが、やっていることは２次元のパターンと変わらないです。ただ、次元が大きくなるとヘッセ行列を手計算で求めるのは限界がありますね。
さて、ラグランジュ関数の極値を求めるには、${L(x1, x2, …、xn, λ1,λ2,…、λm)}$の偏微分をゼロに設定し、${x_1、x_2、…、xn、\lambda_1、\lambda_2、…、\lambda_m}$について解きます。
さて、ここまでに計算手順を順に並べてみましょう。
計算の手順
- ラグランジュ関数を作る – 目的関数と制約条件を使って、1つの関数にまとめる。
- 偏微分して式を立てる – 各変数について微分して、それがゼロになるようにする。
- 連立方程式を解く – 得られた式から、目的関数を最大（または最小）にする変数の値を求める。
ラグランジュの未定乗数法の応用例
経済学における応用問題
経済学では、ラグランジュの未定乗数法は、資源制約の下での効用最大化問題や利潤最大化問題を解決するために使用されます。
例えば、消費者は、予算制約の下で、効用（満足度みたいなもん）を最大化する消費量を選択する必要があります。
この問題を解決するために、ラグランジュの未定乗数法が使用されます。
実際に解いてみましょう。
レベルとしては、統計検定1級応用の社会科学分野くらいです。
ある消費者の効用関数が${U(x,y) = 3x^{0.5}y^{0.5}}$で表されるとします。ここで${x}$は食料への支出、${y}$は娯楽への支出を表します。 予算制約式は${2x + 3y = 300}$（単位：千円）で表されます。
(1) この消費者の効用を最大化する${x}$と${y}$の値を求めてください。
(2) 最適な消費量での限界代替率を求めてください。
(3) このとき、所得の限界効用（ラグランジュ乗数${\lambda}$の値）を求め、その経済学的意味を説明してください。
コブダグラス型の効用関数ですね。経済系の学部だとよく見ると思います。
予算制約〜、とか出る場合は今回の未定乗数法を思い浮かべてほしいです。
経済学における応用問題｜回答
まずは、ラグランジュ関数を設定します。
目的関数：U(x,y) = 3x^{0.5}y^{0.5}（最大化したい）
制約条件：2x + 3y = 300（予算制約）
予算制約の式から、以下のようなラグランジュ関数が設定できます。
$${L(x,y,\lambda) = 3x^{0.5}y^{0.5} + \lambda(300 – 2x – 3y)}$$
では、一階条件（偏微分）の計算です。
$${\partial L/\partial x = \frac{3}{2}x^{-0.5}y^{0.5} – 2\lambda = 0… (1)}$$
$${\partial L/\partial y = \frac{3}{2}x^{0.5}y^{-0.5} – 3\lambda = 0… (2)}$$
$${\partial L/\partial \lambda =300 – 2x – 3y = 0 … (3)}$$
で、連立方程式を解くと${(x,y)=(75,50)}$がもとまりました。（問い１の答え）
予算制約に${(x,y)}$を代入すると${\lambda=0.5}$となりました。
では、問い２の限界代替率を考えてみましょう。
$${MRS = \frac{2}{3}}$$
これは、食料支出を1単位減らすとき、効用水準を維持するために必要な娯楽支出の増加量が${2/3}$単位であることを示します。（問い２の答え）
さて、限界効用は${\lambda}$ですが、しっかりと条件を確認しましょう。
$${∂²L/∂x² = (-3/4)x^{-3/2}y^{1/2}}$$
$${∂²L/∂y² = (-3/4)x^{1/2}y^{-3/2}}$$
$${∂²L/∂x∂y = (3/4)x^{-1/2}y^{-1/2}}$$
より、ヘッセ行列を作成します。
$${H = \begin{pmatrix} \frac{\partial^2 L}{\partial x^2} & \frac{\partial^2 L}{\partial x\partial y} \\ \frac{\partial^2 L}{\partial x\partial y} & \frac{\partial^2 L}{\partial y^2} \end{pmatrix}}$$
これらを${(x,y)=(75,50)}$で評価し、ヘッセ行列が負定値であることを確認
$${H = \begin{pmatrix} -0.00183 & 0.00224 \\ 0.00224 & -0.00275 \end{pmatrix}}$$
ヘッセ行列が負定値であることを確認できたので、極大値であることの確認ができました。
よって、限界効用は0.5です（問い３の答え）
解釈については、以下のようになります。
最適解の解釈：食料支出75千円、娯楽支出50千円
限界効用λ = 0.5 の解釈：予算が1単位（1000円）増えると効用が0.5単位増加
限界代替率${\frac{2}{3}}$の計算と解釈：食料支出1単位減少に対し、娯楽支出2/3単位の増加で効用水準が維持される
