正規分布とは?図解と合わせわかりやすく解説
こんにちは、青の統計学です。
二項分布やポアソン分布のようなカウントデータを扱う離散分布の他に、連続データを扱う連続分布があります。
今回は、連続分布の代表格である「正規分布」について扱います。
確率密度に関する例題とともに、分布の再生性についても取り上げます。
正規分布(gaussian distribution)
正規分布(ガウス分布)は、釣鐘型の形をした連続型の確率分布です。Rではこのように表すことができます。
y <- seq(-5,5,0.1)
plot(y,dnorm(y ,mean=0,sd=1),type="l")seq()で、-5から5までで0.1刻みの値を代入します。
dnorm(y, mean=0,sd=1)は、正規分布の確立密度を表すコードです。
meanは平均で、sd(standard deviation)は標準偏差を表しています。
平均0で分散1の正規分布を、標準正規分布と呼びます。
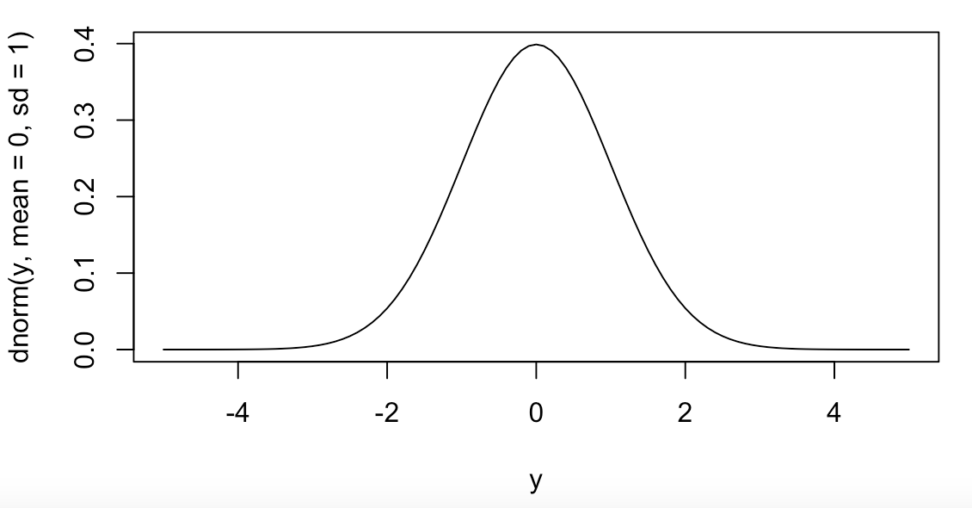
確率密度関数
標準正規分布の確率密度関数は、やや複雑な形をしています。ちなみに、大学のテストでは問題用紙に書いてあることがほとんどです。
$$f(x)= \frac{1}{\sqrt{2π}}exp(- \frac{x^2}{2})$$
xは-∞から∞の値を取ります。
分布は、\(N(μ,σ^2)\)と表し、\(μ\)は平均で\(σ^2\)は分散を表します。
上の確率密度関数は\(μ=0\)で\(σ^2=1\)の標準正規分布のものです。
一般形は以下の形を取ります。
$$f(x)= \frac{1}{\sqrt{2πσ^2}}exp(- \frac{(x-μ)^2}{2σ^2})$$
正規分布のモーメント母関数についての導出は以下のコンテンツをご覧ください。
【統計検定】確率分布のモーメント(積率)母関数完全ガイド|導出チートシート
密度を求める(density)
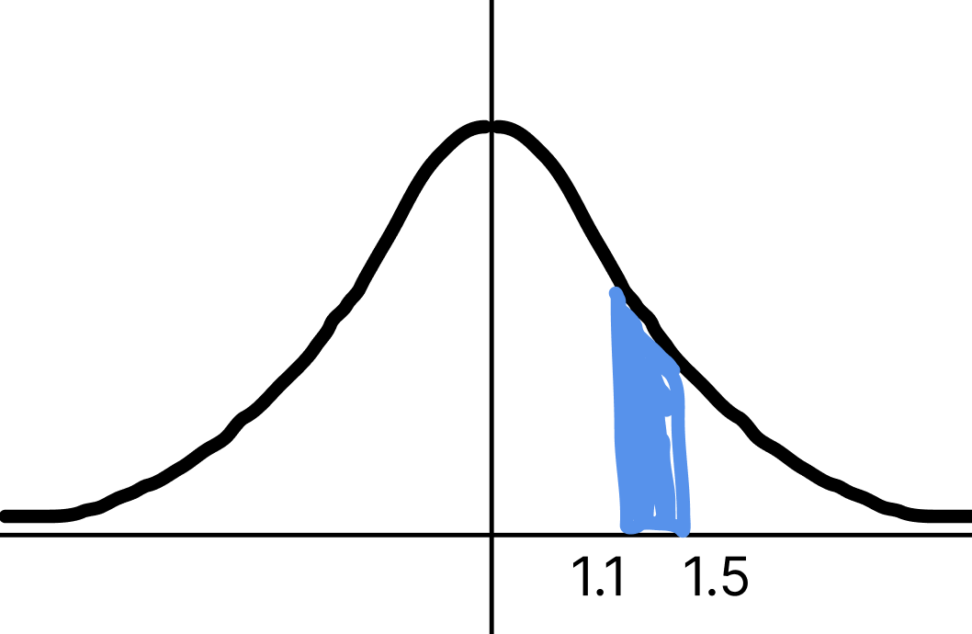
連続データを扱う確率は、密度で表します。例えば、確率変数が1.1から1.5までの確率を求めます。数式は以下の通りです。
$$\displaystyle \int_{1.1}^{1.5}p(y|μ,σ)dy$$
平均と標準偏差がわからないと計算できないので、仮に平均1で標準偏差が1の標準正規分布とします。
$$\displaystyle \int_{1.1}^{1.5}p(y|0,1)dy$$
Rで書くとこのようになります。pnorm(x,μ,sd)は-∞からxまでの正規分布の密度を求めます。
μは0で、sdは1ですね。求めたい面積は、差を取る必要があります。
pnorm(1.5,0,1)-pnorm(1.1,0,1)
[1] 0.06885886確率は0.069くらいになりました。
正規分布に関わる問題をときましょう
Yが正規分布\(N(50,10^2)\)に従うとき、に上側1%点を求めてみましょう。
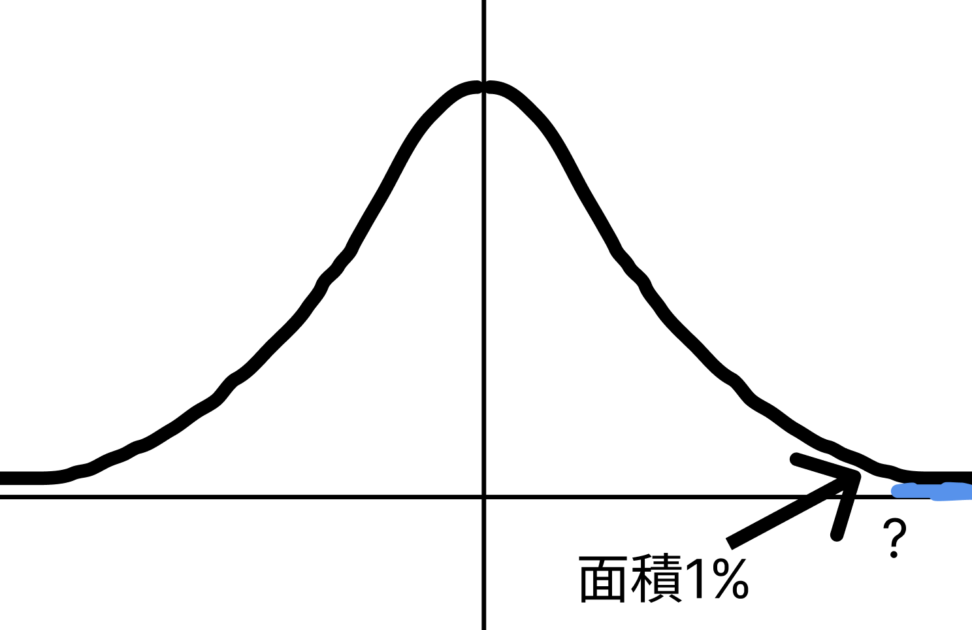
【解説】問題の意味はわかりましたでしょうか。上画像の青色部分が全体の面積の1%になるような値を求める問題でした。
0.01 = P(Y ≧ y)となるyを求めるために、まずは正規化を行う必要があります。
$$P(Y≧ y) =P(\frac{Y-50}{10} ≧ \frac{y-50}{10})$$
確率変数から平均を引き、標準偏差で割ると、標準偏差の確率変数Zになります。
この行為を正規化と呼びます。ここでは、平均の50を引き、標準偏差の10で割ります。
$$P(Y≧ y) =P(Z≧\frac{y-50}{10})$$
$$P(Z≧ \frac{y-50}{10}) = 1-Φ(\frac{y-50}{10})$$
そして確率は、1から「-∞からy(求めたい値)までの確率」の差になります。
ここが一番わかりにくいと思います。全体の確率から、左から確率99%を引いて1%としています。
| z | 0.0 | 0.01 | 0.02 | 0.03 |
| 1.0 | 0.15866 | 0.15625 | 0.15386 | 0.15151 |
| 1.1 | 0.13567 | 0.13350 | 0.13136 | 0.12924 |
| 1.2 | 0.11507 | 0.11314 | 0.11123 | 0.10935 |
| 1.3 | 0.09680 | 0.09510 | 0.09342 | 0.09176 |
| 1.4 | 0.08076 | 0.07927 | 0.07780 | 0.07636 |
| 1.5 | 0.06681 | 0.06552 | 0.06426 | 0.06301 |
| 1.6 | 0.05480 | 0.05370 | 0.05262 | 0.05155 |
| 1.7 | 0.04457 | 0.04363 | 0.04272 | 0.04182 |
| 1.8 | 0.03593 | 0.03515 | 0.03438 | 0.03362 |
| 1.9 | 0.02872 | 0.02807 | 0.02743 | 0.02680 |
| 2.0 | 0.02275 | 0.02222 | 0.02169 | 0.02118 |
| 2.1 | 0.01786 | 0.01743 | 0.01700 | 0.01659 |
| 2.2 | 0.01390 | 0.01355 | 0.01321 | 0.01287 |
| 2.3 | 0.01072 | 0.01044 | 0.01017 | 0.00990 |
| 2.4 | 0.00820 | 0.00798 | 0.00776 | 0.00755 |
最後に正規分布表を見て、0.01(1%)を探します。2.33だとわかりました。
$$\frac{y-50}{10}=2.33$$
最後に上の方程式を解いておしまいです。答えは、73.3です。相当高いですね。
お気づきの方も多いですが、これは偏差値の計算方法です。偏差値73あたりを取るのは全体の上位1%ということになります。
ただし、平均が50で分散が100という前提を置いています。
正規分布の再生性
補足ですが、正規分布には「再生性」という便利な特徴があります。
ポアソン分布には、「再生性」という嬉しい特性があります。
再生性とは、「確率変数同士を足しても、その分布がわかる」という特性です。
以下、命題です。
命題 1:X1とX2は独立 2:X1 ~ N(μ1, σ1^2) 3:X2 ~ N(μ2, σ2^2) ならば、X1 + X2 ~ N(μ1 + μ2, σ1^2 + σ2^2)が成り立つ。
つまり、X1とX2という独立した確率変数がそれぞれ正規分布に従っている場合には、その確率変数の和自体も、期待値が(μ1 + μ2)で分散が(σ1^2 + σ2^2)とする正規分布に従います。
もっと汎用的な話としては、以下のようになります。
X1,X2,‥,Xn ~ N(μ,σ^2)で独立かつ同一の分布に従うとき、 Wn = X1 + X2 + ‥ + Xn ~ N(nμ, nσ^2)
和の分布も当然正規分布分布に従います。期待値はnμであり、分散はnσ^2です。
では、再生性があると何が嬉しいのかというと、例えば
標本平均の分布が正確にわかる
ということが挙げられます。
$$\overline{X} = \frac{W_{n}}{n}〜N(μ,\frac{σ^2}{n})$$
標本平均の分布を求めることができました。
この式は標準化することが多いです。下の式の方がよく見たことがあると思います。
$$\sqrt{n}\frac{\overline{X}-μ}{σ}〜N(0,1)$$
標準化された標本平均は標準正規分布に従うことがわかります。
この証明には、再生性という正規分布の特性が使われていました。余裕があれば覚えておきましょう。
正規分布以外にも、ポアソン分布やベルヌーイ分布にも再生性はあります。
ポアソン分布について詳しく知りたい方は、以下のコンテンツをご覧ください。
標準正規分布と比較した統計量である、歪度と尖度やモーメント母関数については、以下のコンテンツをご覧ください。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!






