【例題あり】一様分布についてわかりやすく解説

一様分布

一様分布は最もシンプルな連続確率分布の一つで、「同じ確率で起こる」という直感的な概念を数学的に表現したものです。

例えばこんな感じです。

• サイコロの目の出る確率
• ランダムな時刻に電車が到着する待ち時間（特定の時間帯内）
• 製造誤差が許容範囲内でランダムに発生する場合

では、早速みていきましょう。

連続型一様分布

一様分布の特徴の一つが、連続型と離散型どちらもある、という点です。

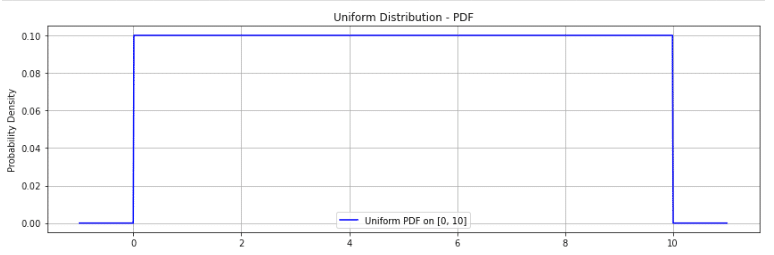
さて、連続型一様分布では、ある区間 ${[a, b]}$の中で、全ての値が均等な確率で出現する分布です。

区間 $[a,b]$ 上の一様分布の確率密度関数 $f(x)$ は

$${f(x) = \begin{cases} \frac{1}{b-a} & (a \leq x \leq b) \\ 0 & (\text{otherwise}) \end{cases}}$$

${a}$ と ${b}$ は区間の下限と上限で、${a < b}$。

面積が1になるように ${\frac{1}{b-a}}$という高さになります。

連続型一様分布｜累積分布関数

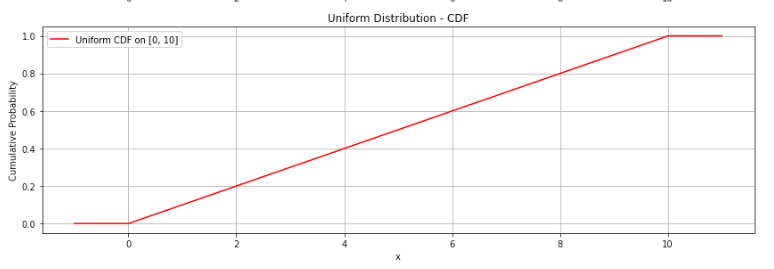
一様分布に限らないですが、累積分布関数 ${F(x)}$は、確率変数 ${X}$ がある値以下になる確率を表します。

なので、累積分布関数 $F(x)$ は

$F(x) = \begin{cases} 0 & (x < a) \\ \frac{x-a}{b-a} & (a \leq x \leq b) \ 1 & (x > b) \end{cases}$

となります。

どの実現値も同様に起こりやすいため、下のように累積分布関数が線形に1に向かっていくことがわかります。

連続型一様分布｜期待値と分散

• 期待値：$E[X] = \frac{a+b}{2}$
• 分散：$V[X] = \frac{(b-a)^2}{12}$

さて、覚えるのも良いですがこのくらいはできるようになりたいですね。

分散だけ導出してみましょう！

分散の導出

区間$[a,b]$の連続一様分布において、

まず、確率密度関数$f(x)$は以下のように定義されます

$$f(x) = \begin{cases} \frac{1}{b-a} & (a \leq x \leq b) \ 0 & (otherwise) \end{cases}$$

$E[X^2]$を計算します

${E[X^2] = \int_{a}^{b} x^2 \cdot \frac{1}{b-a} dx}$

${= \frac{1}{b-a}[\frac{x^3}{3}]_{a}^{b}}$

${= \frac{1}{b-a}(\frac{b^3}{3} – \frac{a^3}{3})}$

${= \frac{b^3-a^3}{3(b-a)}$ $= \frac{a^2+ab+b^2}{3}}$

$(E[X])^2$を計算します

$$(E[X])^2 = (\frac{a+b}{2})^2 = \frac{a^2+2ab+b^2}{4}$$

したがって、分散は

$V[X] = \frac{a^2+ab+b^2}{3} – \frac{a^2+2ab+b^2}{4}$

$= \frac{4(a^2+ab+b^2)-3(a^2+2ab+b^2)}{12}$

$= \frac{a^2-2ab+b^2}{12}$

$= \frac{(b-a)^2}{12}$

よって、連続一様分布の分散は$\frac{(b-a)^2}{12}$と求めることができました。

分散や期待値から復習したい方は青の統計学のこちらがおすすめです。

離散型一様分布

さて、離散型一様分布では、ある範囲の整数値 ${{x_1, x_2, \dots, x_n}}$ がすべて同じ確率で選ばれる分布です。

連続型と同じようにまずは質量関数から載せていきます。

確率変数$X$が取りうる値を$x_1, x_2, …, x_n$とすると、 確率質量関数は、以下のようになります。

$${P(X = x_i) = \begin{cases} \frac{1}{n} & (x = x_i, i = 1,2,…,n) \\ 0 & (\text{otherwise}) \end{cases}}$$

累積分布関数

$F(x) = P(X \leq x) = \frac{k}{n}$ ここで、$k$は$x$以下の値の個数です。

$k$を$x_k \leq x < x_{k+1}$を満たす整数として

$${F(x) = \begin{cases} 0 & (x < x_1) \\ \frac{k}{n} & (x_k \leq x < x_{k+1}) \ 1 & (x \geq x_n) \end{cases}}$$

例えばサイコロの場合、以下のようになります。

$F(3.5) = P(X \leq 3.5) = P(X = 1) + P(X = 2) + P(X = 3) = \frac{3}{6} = 0.5$

離散型確率分布の期待値と分散

• 期待値：$E[X] = \frac{1}{n}\sum_{i=1}^n x_i$
• 分散：$V[X] = \frac{1}{n}\sum_{i=1}^n (x_i – E[X])^2$

確率積分変換の例題

さて、ここでは一様分布を使った問題をご紹介します。

統計検定準一級から一級レベルです。社会科学分野で出ましたね！

ここでの方針を先に書いておきます。

では、解答例です。

(1) 確率変数 ${X}$の累積分布関数 ${F(x)}$ を求める

累積分布関数 ${F(x)}$ は、確率密度関数 ${f(x)}$ を用いて次のように定義されます。

$${F(x)=P(X\leq x)=\int_{-\infty}^x}f(t)df$$

問題を見ると、確率密度関数 $f(x)$ は次のように与えられています

$f(x) = \begin{cases} 2x, & 0 \leq x \leq 1, \\ 0, & \text{otherwise}. \end{cases}$

したがって、累積分布関数 $F(x)$ を求める際に、範囲ごとに計算します。

$x < 0$について

$${F(x) = 0}$$

累積確率は当然0ですね。

$0 \leq x \leq 1$について

$${F(x) = \int_0^x 2t dt}$$

積分を計算すると$\int 2t dt = t^2$なので、

$${F(x) = [t^2]_0^x = x^2}$$

$x > 1$について

$${F(x) = 1}$$

$f(x) = 0$ なので、累積分布関数は最大値 1 に達します

(2) 新しい確率変数 ${U = F(X)}$ が一様分布${U(0,1)}$に従うことを示す

さて、まずは$U$ の定義による累積分布関数を求めていきましょう。

新しい確率変数 $U = F(X)$ の累積分布関数 $G(u)$ は、次のように表されます

$${G(u) = P(U \leq u)}$$

これはU = F(X)$ より、$G(u) = P(F(X) \leq u)$ですね！

では、$F(X) \leq u$ を $X$ の範囲に変換します。

累積分布関数 $F(x)$ は単調増加であるため、$F^{-1}(u)$ を適用できます（大事！）

$F(X) \leq u \Rightarrow X \leq F^{-1}(u)$

ここで、累積分布関数 $F(x)$ の逆関数 $F^{-1}(u)$ を計算します。

$F(x) = x^2$ の範囲は $0 \leq x \leq 1$ なので

$${u = x^2 \Rightarrow x = \sqrt{u}$ $(0 \leq u \leq 1)}$$

よって、$F^{-1}(u) = \sqrt{u}$ です。

$P(F(X) \leq u)$ は $P(X \leq F^{-1}(u))$ に変換されるため

$${G(u) = P(X \leq \sqrt{u})}$$

$${P(X \leq \sqrt{u}) = F(\sqrt{u})}$$

累積分布関数 $F(x)$ は $x^2$ で与えられているので、$F(\sqrt{u}) = (\sqrt{u})^2 = u$であり、従って

$${G(u)=u}$$

となりました！