【MCMC】ハミルトニアンモンテカルロによるサンプリングについて|ベイズ統計学
こんにちは、青の統計学です。
今回は、以前のコンテンツで紹介しきれなかったハミルトニアンモンテカルロを使った事後分布のサンプリングについてご紹介していきます。
ハミルトニアンモンテカルロ(Hamiltonian Monte Carlo
ベイズ統計学において、ハミルトニアンモンテカルロ(Hamiltonian Monte Carlo, HMC)を利用するアプローチは、主に複雑な事後確率分布からの効率的なサンプリングに用いられます。
このプロセスを理解するためには、ベイズの定理とハミルトニアンの動力学の基本概念を組み合わせる必要があります
おさらい|ベイズの定理
ベイズの定理について、具体例を元に解説した、より平易なコンテンツは以下になります。
さて、ベイズ推量の世界では、全ての確率は主観的な確率 (subjective probability) だとされています。
普通、確率というのは対象の不確かさを示す量とされますが、ベイズ推量では不確かさはその対象を観測する人の知識にあると考えており、それを主観確率と呼んでいます。
では、事前確率と事後確率について説明します。
ベイズの定理で使う事前確率 Pr(X) とは、観測者が観測以前に持っている主観確率を確率分布関数で表現したものです。
ちなみに、事前分布に無情報一様分布を設定すると、事後分布と尤度関数が一致するので、MAP推定量は最尤推定量と一致します。
この辺りは頻度論と整合性があって素敵ですね。
一方、事後確率はなんでしょうか?
例えば、観測した結果を \(D\) とします。
観測結果 \(D\) によって、確率変数 \(X\) に関する主観確率が変化します。
観測結果 \(D\) のもとで確率変数 \(X\) に関する主観確率を \(Pr(X|D)\) と書き、事後確率 (posterior) と呼んでいます。
この事後確率分布を求めるのがベイズ推量の目的です。
おさらい|尤度
ベイズ統計では、尤度という概念が必要です。
詳しく知りたい方は以下のコンテンツをご覧ください。
【AICで使う】KL divergence(カルバック-ライブラー情報量)をわかりやすく解説|python
確率変数 X(以後パラメータと呼びます) の元では、観測結果 \(D\) が確率 \(Pr(D|X)\) に従って生成されるはずであることが分かっていたとします。
\(Pr(D|X)\) を \(D\) が観測された時の \(X\) の尤度 (likelihood) と呼びます。
さて、これまで紹介した事前確率 \(Pr(X)\)、事後確率 \(Pr(X|D)\)、尤度 \(Pr(D|X)\) の間には以下の関係が成り立ちます。
$$P(X|D)=\frac{Pr(D|X)Pr(X)}{\int Pr(D|X)Pr(X)}$$
これをベイズの定理と呼びます。
また分母の値を特に エビデンス(evidence) と呼びます。
ベイズ統計では、データを元にしてどんどん事後分布を更新していくアプローチを取ります。
おさらい|MCMC法
パラメータの数が増えると、共同事後分布の複雑さが増し、サンプリングが難しくなります。
なので、まずモンテカルロ法というランダムなサンプリング法を考えてみます。
統計検定準1級でも、正方形の中に90度の扇形を入れて、ランダムにサンプリングして、円の面積を求めていくという問題がありました。
このように、乱数を用いた試行を繰り返すことで近似解を求める手法で、確率論的な事象についての推定値を得る場合を特に「モンテカルロシミュレーション」と呼びます
では、単純モンテカルロ積分を見てみましょう。
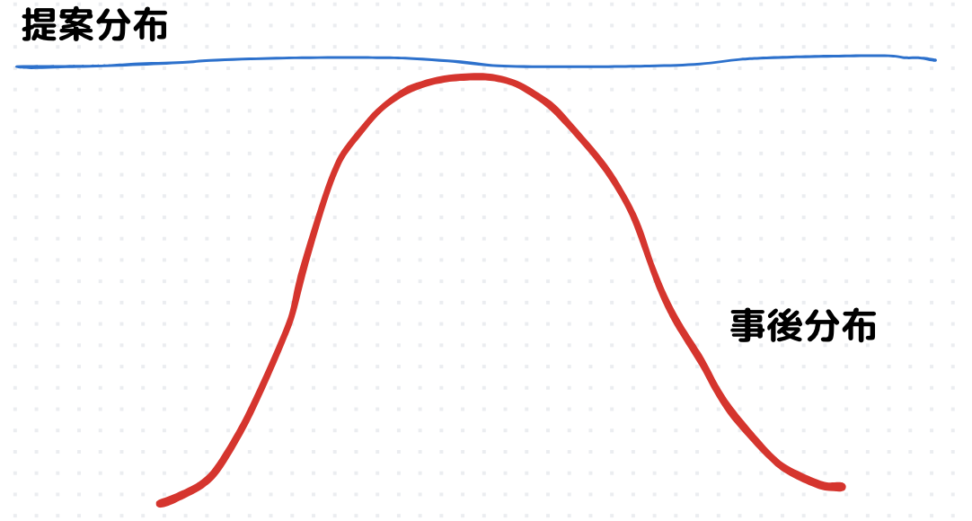
提案分布を一様分布\(U(0,1)\)として、提案分布から乱数\(X〜N(0,1)\)を発生させていきます。
\(g(x)\)はよくわからないので、それを覆うような提案分布からサンプリングしていくということですね。
$$θ=\int_{0}^{1}g(x)dx$$
モンテカルロ積分は事後確率分布 \(Pr(X|D)\) からサンプル \(X\) を取り出すことで期待値\(E[g(X)]\)を近似値的に評価していきます。
大数の弱法則により、サンプリング回数が無限大になると、\(θ\)に確率収束します。
$$E[g(X)]=\hat{θ}=\frac{1}{n} \int_{0}^{1}g(X_i)dx$$
ランダムサンプルを生成して、それらの平均を取ることで積分値を近似します。
ただし、問題点があります。
1回ごとのサンプリングが独立なので、高次元だと殆ど棄却されてしまうのです。
高次元になると、提案分布に対して採択される的が小さいイメージを持っていただけると良いと思います。
高次元空間では、分布が疎になることが多く、効率的なサンプリングが困難になる可能性があるということですね。
これを次元の呪いと呼びます。
多項式曲線のフィッティングの問題ですね、係数の数が冪乗に増加していき、高次元になると幾何的な直感が当たらないです。
では効率よくサンプリングするには、一期前のサンプリングを使えば良いのではという発想が自然と生まれるはずです。
これが、マルコフ連鎖モンテカルロ法の着想です。
ハミルトニアン力学の話
さて、HMCに話を戻します。
ハミルトニアンモンテカルロ(Hamiltonian Monte Carlo, HMC)に関してきっちり理解を得るためには、まず物理学におけるハミルトニアンの概念についての基礎知識が必要です。
ハミルトニアン(系の全エネルギー)は、物体のエネルギーを記述するための関数であり、力学的エネルギーの総和、すなわち運動エネルギーと位置エネルギー(ポテンシャルエネルギー)の和として表されます。
ハミルトニアン \(H\) は、運動量 \(p\) と位置 \(q\) を使って次のように表されます
$$H(p,q)=T(p)+V(q)$$
ここで、\(T(p)\)は運動エネルギー(例えば\(\frac{p^2}{2m}\))、\(V(q)\)は位置エネルギーを示します。
物体の運動を追跡するには、ハミルトンの正準方程式を解く必要があります。
これらは、時間に関して運動量と位置の導関数を与えるもので、以下の形で表されます。
$$\frac{dq}{dt}=\frac{∂H}{∂p}$$
$$\frac{dp}{dt}=-\frac{∂H}{∂q}$$
ハミルトニアンモンテカルロでは、このハミルトンの正準方程式を用いて、高次元の確率分布に沿った効率的な探索を実現します。
もう少し詳細に説明すると、この正準方程式は系の状態が時間と共にどのように変化するかを記述しているので、正準方程式を解くことで、物理的に意味のある方法(エネルギー保存の原則に従う)でパラメータ空間を探索できます。
これにより、効率的かつ効果的にターゲット分布からのサンプリングが可能になります。
HMCのアプローチ
MCMCと同様にやりたいことは、事後確率分布 \(P(\theta|D)\)からサンプリングです。
しかし、直接サンプリングするのは難しいため、ハミルトニアン力学を用いてこの問題を解決します。
先ほどのハミルトニアン方程式は、ベイズ統計の文脈だと以下のように解釈します。
$$H(\theta|p)=T(p)+V(\theta)=T(p)-log(P(\theta|D))$$
ベイズ文脈では、ポテンシャルエネルギーは通常、負の対数事後確率(尤度と事前確率の負の対数の合計)として定義されます。
また、\(T(p)\)は運動エネルギーを表し、通常、運動量の二次形式として定義されます。
ここで\(p\)は運動量のベクトルです。
次に正準方程式についてです。
パラメータ \(\theta\)と運動量\(p\) の時間発展は、以下の正準方程式によって記述されます:
$$\frac{d \theta}{dt}=\frac{∂H}{∂p}$$
$$\frac{dp}{dt}=-\frac{∂H}{∂ \theta}$$
このあとは、数値積分を行います。
上の方程式は通常、リープフロッグ法と呼ばれる数値積分法を用いて近似的に解かれます。
これにより、新しいパラメータと運動量の候補が提案されます。
leap flog法
リープフロッグ法は、数値解析のアルゴリズムで、特に微分方程式の解を近似的に求める手法として重要です。
リープフロッグ法は、オイラー法よりも高精度な方法であり、特に振動系や保存系のシミュレーションに適しています。
この方法は、半ステップずつ進むことで、オイラー法の数値不安定性を改善しています。
リープフロッグ法は次のような手順で進行します。
まず、位置 \(q\) と運動量 \(p\)を初期化し、次に以下のステップを繰り返します。
1:半ステップの時間 \(\frac{h}{2}\)で運動量 \(p\)を更新する。
2:完全なステップの時間 \(h\)で位置 \(q\) を更新する。
3:さらに半ステップの時間 \(\frac{h}{2}\)で運動量 \(p\)を再び更新する。
これにより、次の時間ステップにおける \(q\)と\(p\) の値を得ます。数学的には、以下の式で表されます。
$$p_{n+\frac{1}{2}}=p_n+\frac{1}{2}×f_q(q_n,p_n)$$
$$q_{n+1}=q_{n}+h×f_p(q_{n},p_{n+1})$$
$$p_{n+1}=p_{n+\frac{1}{2}}+\frac{h}{2}×f_q(q_{n+1},p_{n+1})$$
正準方程式を解くことで得られた新しい状態\(p,q\)が得られた後、それを受容するかどうかというプロセスに移ります。
受容確率は以下のようになります。
$$min(1,exp(-H(\theta’,p’)+H(\theta,p)))$$
新しい状態を受容するかどうかは、メトロポリス基準(一定の確率で受容・拒否)によって決定されます。
この確率は、新しい状態が古い状態よりも低いハミルトニアン(すなわち低いエネルギー)を持つ場合に高くなります。
そして上のプロセスを繰り返し、多数のサンプルを生成します。
これにより、事後分布の表現が得られます。
→というのも詳細釣り合いの原則があるからですね。
メトロポリス受容ステップは、マルコフ連鎖が詳細釣り合いの原則を満たすことを保証します。
これにより、長期的にはターゲット分布に従ったサンプリングが保証されます。
この方法では、ランダムウォークメトロポリスヘイスティングスのように単純なランダムサンプリングに依存せず、複雑な確率分布、特に高次元での探索が効率的に行えます。
HMCの基本的なアイディアは、各反復でランダムに運動量を初期化し、それを使用してハミルトンの正準方程式を数値的に解くことです。
この過程で生成された軌道は、新しいサンプル候補を提供します。
この新しいサンプルは、特定の条件(詳細釣り合い条件など)に基づいて受け入れられるか、拒否されます。
このプロセスは、サンプリングを目指す分布に従って運動量を「誘導」し、より効率的な探索を可能にします。
ただHMCは計算コストが高く、数値積分のためのステップサイズやステップ数などの調整が必要な場合があります。
また、運動量の初期化や数値積分のエラーによっては、提案されたサンプルが拒否される可能性があります。
しかし、これらのデメリットを上回る効率と精度を提供するため、ベイズ統計学において広く利用されています。

