統計検定2級のチートシートと独学で受かるコツ【最短合格】

統計検定2級の基本情報

統計検定2級は、大学基礎科目レベルの統計学の知識の習得とその活用について理解しているか問われる検定です。

取得することで機械学習やデータ分析を行う際に必要な基礎知識が身につきます。

統計検定2級の範囲

統計検定2級は、記述統計から推測統計、回帰分析までとかなり広い範囲を扱います。

効率的な勉強が必要です。

今回は、皆さんの学習をお助けするためのチートシートをご用意しました。

1変数データ	中心傾向の指標、散らばりの指標、中心と散らばりの活用、時系列データの処理
2変数以上のデータ	散布図と相関、カテゴリカルデータの解析、単回帰と予測
標本調査など	観察研究と実験研究、各種の標本調査法、フィッシャーの3原則
確率	統計的推測の基礎となる確率、ベイズの定理
確率分布	各種の確率分布とその平均・分散
標本分布	標本平均・標本比率の分布、二項分布の正規近似、ｔ分布・カイ二乗分布、Ｆ分布
推定	推定量の一致性・不偏性、区間推定、母平均・母比率・母分散の区間推定
仮説検定	ｐ値、2種類の過誤、母平均・母比率・母分散の検定[1標本、2標本]
カイ二乗検定	適合度検定、独立性の検定
線形モデル	回帰分析、実験計画

統計検定2級のチートシート

フィッシャーの3原則

反復（Replication）

同じ条件下で複数回の実験や観測を行うことで、データの信頼性を高めることを目的にしています。

反復により、サンプルサイズが増え、統計的な推論がより正確になるということですね。

ランダム化（Randomization）

実験の対象（例えば、被験者やプロット、時間など）に対する処理をランダムに割り当てる行為です。

ランダム化により、未知または制御できない外的要因による影響を平均化し、バイアスを減らすという恩恵があります。

局所制御（Local Control）

実験条件や観測条件をできるだけ一定に保ち、他の影響因子の効果を最小限に抑えるということです。

これはブロック化や共変量調整など、実験設計において他の方法と組み合わされることもあります。例えば肥料による効果が知りたい場合に、土の状態や日当たりが異なっていては結果の解釈ができないということですね。

コラム｜バイアスとは

ランダム化の部分で話題に上がった、「バイアス」について皆様はきちんと説明ができるでしょうか？

統計学的には、バイアスは推定量の期待値と真の母数との差として定義されます。

数学的に表現すると以下のようになります

$${Bias(\hat{\theta}) = E[\hat{\theta}] – \theta}$$

• $\hat{\theta}$ は母数 $\theta$ の推定量
• $E[\hat{\theta}]$ は推定量の期待値
• $\theta$ は真の母数の値

バイアスの重要性はなんと言っても、不偏性です。

不偏性は、推定量がバイアスを持たない状態、その推定量は不偏であると言います。

つまり： ${E[\hat{\theta}] = \theta}$ ですね。

不偏推定量は統計学的推論において望ましい性質とされます。

MSE (平均二乗誤差) との関係: バイアスは推定量の精度を評価する上で重要な役割を果たします。

MSEは以下のように分解できます

$${MSE(\hat{\theta}) = Var(\hat{\theta}) + [Bias(\hat{\theta})]^2}$$

この式はバイアス-分散トレードオフとして知られています。

一致性: サンプルサイズが無限大に近づくにつれてバイアスが0に収束する推定量は一致推定量と呼ばれます： $${\lim_{n \to \infty} Bias(\hat{\theta}) = 0}$$

ここまでの話をもっと詳しく知りたい人は、こちらをどうぞ！

決定係数

ほぼ出るでしょう。決定係数は、モデルの説明力を表す指標です。

実務においても、よく出る指標で、1に近いほど評価が高いです(注意事項はあり)

$$R^2 = {\frac{回帰変動}{全変動}}=1-{\frac{残差変動}{回帰変動}}$$

全変動：\(\sum_{i=1}^N(y_{i}-{\overline{y}})^2\)

回帰変動：\(\sum_{i=1}^N(\hat{y}_i-{\overline{y}})^2\)

残差変動：\(\sum_{i=1}^N(y_{I}-{\hat{y}})^2\)

モデルの説明変数が増えるほど当てはまりはよくなるので、モデルの複雑さとのトレードオフになります。

特に説明変数の数が異なる回帰モデル同士を比較する場合には、自由度修正済み決定係数を使用します。

$$adjustedR^2 = 1-{\frac{\frac{\sum_{i=1}^{N}(y_{i}- \hat{y}_{i})^2}{n-d-1}}{\frac{\sum_{i=1}^{N}(y_{i}-{\overline{y}})^2}{n-1}}}$$

決定係数は、割と理解しやすくビジネスの場でもよく使われますが、注意点があります。

以下の通りです。

これらの欠点に対処するため、ロバスト統計や非線形モデリング技術が用いられることがあります。

多重共線性などは、統計検定準一級で話題になりますね。

詳しくは以下のコンテンツでご覧ください。

データサイエンティストの実務でも必要な技能なので、しっかり押さえておきましょう。

---

第一種の過誤と第二種の過誤

こちらは、統計的仮説検定において特に重要な概念ですね。

p値と同じく誤解しやすいポイントなので、注意が必要です。

\(\alpha\)：第一種の過誤の確率、帰無仮説\(H_0\)が真の場合に誤って帰無仮説を棄却してしまう確率

→正規分布表を参照し、\(Z_\alpha\)を求める

\(\beta\)：第二種の過誤の確率、対立仮説\(H_1\)が真の場合に誤って帰無仮説を採択する確率。

→正規分布表を参照し、\(Z_\beta\)を求める

基本的に\(\alpha\)が大きくなると、\(\beta\)は小さくなるという負の相関があります。

\(1-\beta\)：検定力、対立仮説が真の場合に帰無仮説を正しく棄却する確率。

結局何が言いたいか：一定以下の\(\alpha\)で検出力が最大の区間が一番いい区間です。

なのでよく問題で有意水準を基準に問題を設定しています。

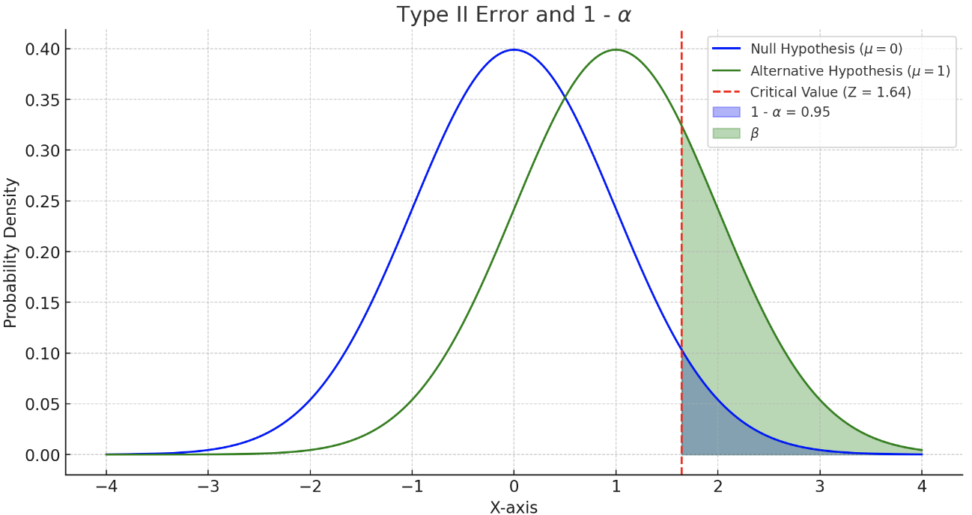
\(\beta\)は\(H_1\)をもとに設定、\(\alpha\)は\(H_0\)をもとに設定するので 、上のような関係になります。

対象としている分布が違うということですね。

もっと詳しく勉強したい方は、この辺りのコンテンツをご覧いただくと良いと思います！

ちなみに統計検定準一級だと、有意水準と検定力を指定して、必要なサンプル数を算出するサンプルサイズ設計を扱う問題が出たりします。

---

コラム｜p値

このコラムは、チートシートというよりもp値に関して、一人でも多くの方に正しい理解をしてほしいため載せたものになります。

統計検定2級でも必須の知識ですので、ぜひ目を通していただければと思います。

さて、p値は「帰無仮説が正しいと仮定した場合に、観測されたデータやそれ以上に極端なデータが得られる確率」として定義されています。しかし、ここで強調すべきなのは、「p値が帰無仮説の真偽を直接示すものではない」という点です。

p値は、あくまでデータと帰無仮説の一致性を評価する指標と考えるべき、ということですね。

なので、「統計学的有意差がある」という表現と「P<0.05」という表現を同じ意味で扱うのは、結果の解釈を過度に単純化しています。

上記↑の理解がややこしいのが、統計的推論の問題設定でもよくある「p<0.05」という閾値を基に結果の「有意性」を判断する、というのが一般的だからですよね。

実はこの表現は、必ずしも結果を説明する最良の方法とは言えないのです。

また「p値が小さくても、帰無仮説が信じがたい場合や、単に仮説が間違っている場合がある」ということにも注意が必要です。特に、サンプルサイズが大きい場合には、統計的には「有意」な結果が得られたとしても、実際には意味のない小さな効果であることがしばしばあります。

まあそもそも、妥当な別の仮説を立てた場合、その仮説に対するp値がさらに低くなる可能性もあるので、複数の競合する仮説を検討するのが、良い分析者の第一歩だと思います。

---

分散分析

統計検定2級で最も厄介なのが、分散分析だと思います。

まず、気をつけていただきたいのが、帰無仮説と対立仮説の立て方です。

自由度の理解

自由度は、分散分析において重要な役割を果たします：

• 水準の自由度 ${v_B}$：${水準数 – 1}$
• 全体の自由度 ${v_T}$：${サンプル総数 – 1}$
• 残差の自由度 ${v_W}$：${全体の自由度 – 水準の自由度 = v_T – v_B}$

交互作用を含む場合（例：A×B）、その自由度は各主効果の自由度の積となります： ${v_{A×B} = v_A × v_B}$

平方和の計算

水準間平方和（SSB: Sum of Squares Between groups）

$${SSB = \sum_{i=1}^{k} n_i (\bar{X}_i – \bar{X})^2}$$

ここで、

• ${k}$ は水準数
• ${n_i}$ は各水準のサンプル数
• ${\bar{X}_i}$ は各水準の平均
• ${\bar{X}}$ は全体の平均

SSBは、各水準の平均と全体平均の差異を定量化します。

残差平方和（SSW: Sum of Squares Within groups）

$${SSW = \sum_{i=1}^{k} \sum_{j=1}^{n_i} (X_{ij} – \bar{X}_i)^2}$$

ここで、${X_{ij}}$ は ${i}$ 番目の水準の ${j}$ 番目のデータ点です。

SSWは、各水準内でのデータのばらつきを表します。

平均平方（分散）の計算

• 水準間平均平方 ${MSB = \frac{SSB}{v_B}}$
• 残差平均平方 ${MSW = \frac{SSW}{v_W}}$

注目すべき点として、${MSW}$ は母分散の不偏推定量となります。

F値の計算

$${F値 = \frac{MSB}{MSW} = \frac{\frac{SSB}{v_B}}{\frac{SSW}{v_W}}}$$

F値は水準間の変動と水準内の変動の比率を表し、群間の差異の統計的有意性を評価するために使用されます。

F値まできちんと求めて正解しておきたいところです。

---

コラム｜点推定値の95%信頼区間

水準Aの平均値を使って、信頼区間を作ることもできます。

$$\overline{A}±t_{α/2,df}\sqrt{\frac{SSW}{n_A}}$$

ただしt分布の自由度は残差の自由度になります。

標準誤差の方は母分散の不偏推定量を水準のサンプル数で割り、根号をつけます。

おそらくこれが統計検定2級で出る最も難しい問題な気がします

---

t検定

t検定は、二つの群の平均値の差が統計的に有意かどうかを評価するために使用されます。

この検定は、小標本でも適用可能であり、母分散が未知の場合に特に有用です。

では早速検定統計量を見ましょう。

$$t \quad value = \frac{\hat{p} – p}{SE(\hat{p})}$$

標準誤差で帰無仮説の推定量と推定量の差を割っています。

推定誤差の大きさで調整しているという意味から、各説明変数を公平に比較し、計算された回帰係数が0から離れているかを確認するための指標です。

このとき、t分布を参照しますが自由度はサンプル数-1となることに注意してください。

また、重回帰分析における回帰係数\(\beta_1\)の検定については以下のようになります。

$$t \quad value = \frac{\hat{β}_1 – 0}{SE(\hat{β}_1)}$$

この時の自由度は\(n-k-1\)です(kは説明変数の数)

当たり前ですが、t検定はt分布に基づいています。

t分布は正規分布に似ていますが、裾が厚く、自由度によって形状が変化します。

自由度 $\nu$ は一般的にサンプルサイズ $n$ に基づいて決定されます（例：独立サンプルのt検定では $\nu = n_1 + n_2 – 2$）。

この辺りを深掘りしたい方は、以下のコンテンツが便利です。

様々な抽出法について

次は様々な抽出法についてご紹介します。

クラスター抽出

母集団を網羅的に分割して、クラスターを構成した上でその中から抽出されたいくつかのクラスター内の個体全てを調査する方法。

全てっていうのがポイントですね。

系統抽出

母集団を等間隔に分割し、各区間から一定の規則に従って要素を抽出する方法です。具体的には、通し番号を全個体について、1番目を無作為に選んだ後、一定の間隔で抽出するなどの処理があります。

多段抽出法

母集団をいくつかのグループにわけ、そこから無作為にいくつかのグループを選び…を続けていく。

ただし、段数を増やせば高い精度を得られるわけではありません。

層化抽出

母集団を互いに排他的で網羅的な部分集合（層）に分割し、各層から独立に標本を抽出する方法です。

部分母集団が違いに大きく異なるときに、各母集団でサンプルを抽出して標本のバランスを保てます。

男女とかで分けたりしますね。結構一般的な手法です。

例えば、${H}$ 個の層に分割された母集団において、層 ${h}$ からの抽出率を ${f_h = n_h / N_h}$ とします。

母平均 ${\mu}$ の推定量 ${\hat{\mu}_{st}}$ は

${\hat{\mu}_{st} = \sum{h=1}^H W_h \bar{y}_h}$となります。

・${W_h = N_h / N}$ は層 ${h}$ の重み

・${\bar{y}_h}$ は層 ${h}$ の標本平均

層別分析なども同じ考え方です。

Neyman配分などは、準一級で割と出ますね。

---

偏相関係数

偏相関係数とは、\(x\)と\(y\)の相関を求める際に他の変数\(z\)の影響を取り除いた相関係数です。

異なる事象を同じ事象で回帰させた時に、交絡を回避できる〜という文脈で取り上げられます。

例えば、年齢、収入、教育レベルなど、複数の変数がある場面で、年齢と収入の関係性を、教育レベルの影響を取り除いて評価したい場合などに使用します。

$$r_{xy|z}=\frac{r_{xy}-r_{xz}*r_{yz}}{\sqrt{1-r_{xz}}\sqrt{1-r_{yz}}}$$

普通の相関係数と偏相関係数に大きな差がある場合に、他の変数による交絡があると言えますね。

多重共線性や操作変数法などの議論に繋がります。

因果まではわからないですが、実務でもよく使う指標です。

---

2標本の期待値の差の検定

こちらはプールした不偏分散を使うのでなかなか難しいですね。

まずは、大事な仮定から考えていきましょう。

群A（サンプル数m）と群B（サンプル数n）の期待値の差を検定する際の検定統計量tは以下のように定義されます。

$${t = \frac{\bar{X}_A – \bar{X}_B}{\sqrt{S_p^2(\frac{1}{m} + \frac{1}{n})}}}$$

ここで、

• ${\bar{X}_A}$, ${\bar{X}_B}$ はそれぞれ群A、群Bの標本平均
• ${S_p^2}$ はプールされた不偏分散

です。

プールされた不偏分散 ${S_p^2}$ は、両群の分散を加重平均したものです：

$${S_p^2 = \frac{(m-1)S_A^2 + (n-1)S_B^2}{m + n – 2}}$$

ここで、

• ${S_A^2}$, ${S_B^2}$ はそれぞれ群A、群Bの標本分散
• ${m + n – 2}$ は自由度

この式は、各群の分散に対してサンプル数に基づいた重みづけを行い、不偏推定量を得るためのものです。

そもそもの不偏分散については、こちらで解説しています。

では、2群の分散が同じの場合はどうなるのでしょうか？

早速検定統計量をご紹介します。

$$Z=\frac{|\overline{X}-\overline{Y}|-|\mu_1-\mu_2|}{\sigma\sqrt{m-{-1}+n^{-1}}}\sim N(0,1)$$

帰無仮説における期待値の差が0であれば、\(|\mu_1-\mu_2|\)は0になります。

$$\alpha=P(|Z|>C|H_0)=2P(Z>C|H_0)$$

$$\frac{|\overline{X}-\overline{Y}|-|\mu_1-\mu_2|}{\sigma\sqrt{m-{-1}+n^{-1}}}=z_{\frac{\alpha}{2}}$$

$$|\overline{X}-\overline{Y}|=\sigma\sqrt{\frac{m+n}{mn}}z_{\frac{\alpha}{2}}$$

また、Cは２分の\(\alpha\)分位点に一致することになります。

よって、\(Z\)が２分の\(\alpha\)分位点よりも大きい時に、帰無仮説を棄却できます(嬉しい)。

「標準偏差\(\alpha\)」がわからない場合は、どうでしょうか？

基本母集団の分散はわからない場合が多いです。

等分散の仮定を置きつつも、母分散が未知の場合、母分散\(\sigma^2\)を不偏分散に置き換える必要があります。

不偏分散を使えば、置き換えた結果の検定統計量もt分布に従い、かつ不偏分散は自由度(m+n-2)のカイ2乗分布に従います。

今回は、等分散の仮定があるので、2標本を使った不偏分散を作ります。

$$V^2=\frac{1}{m+n-2}(\sum_{i=0}^m(X_i-\overline{X})^2\sum_{i=0}^m(Y_i-\overline{Y})^2)$$

Xの不偏分散とYの不偏分散の加重平均をとっているだけです。簡単ですね。

よって、新しい検定統計量Tは自由度\(m+n-2\)のt分布に従うことがわかりました。

$$T = \frac{|\overline{X}-\overline{Y}|}{V\sqrt{m^{-1}+n^{-1}}}〜t_{m+n-2,\frac{α}{2}}$$

関連記事はこちら

---

ラスパイレス指数とパーシェ指数

知っていると助かる問題があります。

ラスパイレス指数（Laspayres Index）とパーシェ指数（Paasche Index）は、価格指数や数量指数を計算する際に用いられる方法です。

これらの指数は、異なる時点における価格や数量の相対的な変化を測るものですが、計算方法に違いがあります。

ラスパイレス指数

ラスパイレス指数は、基準期\(t=0\)の数量を用いて価格の変化を評価します

$$L = \frac{\sum_{i=1}^{n} p_{i,t} \times q_{i,0}}{\sum_{i=1}^{n} p_{i,0} \times q_{i,0}}$$

\(n\)：商品の数

\(p_{i,t}​\)：t時点での商品i価格

\(q_{i,t}​\)：t時点での商品iの数量

パーシェ指数

パーシェ指数は、現在の期\(t=t\)の数量を用いて価格の変化を評価します。

$$P = \frac{\sum_{i=1}^{n} p_{i,t} \times q_{i,t}}{\sum_{i=1}^{n} p_{i,0} \times q_{i,t}}$$

ラスパイレス指数は基準期の数量で価格の変化を評価しますが、パーシェ指数は現在の期の数量で評価します。

ラスパイレス指数はより保守的な（過去志向の）価格変化の評価を提供する一方、パーシェ指数はより現在志向の評価を提供するという特徴がありますね。

お疲れ様でした。

このチートシートはあくまで簡易版ですので、上位版「完全版｜統計検定2級のチートシート」は以下をご覧いただければと思います。

▶︎統計検定2級チートシートをチェックする