【尤度って?】尤度関数と最尤推定量の解説と例題
確率分布のパラメータ\(θ\)を推定する方法の一つとして、最尤推定というものがあります。
最尤推定には、尤度関数を使うことが必須です。まずは尤度関数については見てみましょう。
尤度(likelihood)について
抑えてほしいのは、尤度は「確率」である、ということです。
パラメーター\(\theta\)が、ある値\(\theta_1\)を取った時の確率のこと。
具体例を挙げると、「コインを100回投げて、50回表になる時の確率」を尤度L(p)、コインを一回投げて表になる確率のことをパラメーターpと当てはめています。
そして最尤法とは、尤度を最大にするパラメーター\(θ\)推定量として採用しようという方法です。
尤度を最大にするとは、以下の図のように「密度関数(面積)がもっとも大きくなるx軸パラメータを採用する」ということです。
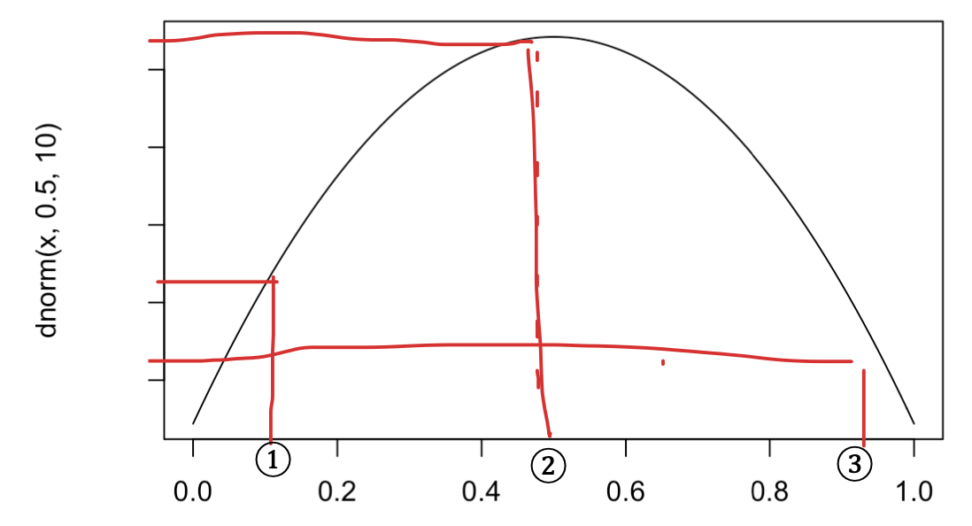
「コインを100回投げて、50回表になる確率の分布」が上の図で表されているとします。
横軸のパラメーターは、コインを一回投げて表が出る確率\(p\)です。
上の図であれば、②が最大の尤度となるので推定量としては\(0.5\)が採用されるということになります。
現実に分析する事象はもっと複雑なので、尤度関数を使います。
尤度関数(likelihood function)
先ほどの尤度を一般化すると、「得られた標本が確率分布Fによってどれだけ生成されやすいのかの指標」と言えます。
そして尤度関数とは、「パラメータ\(\theta\)の推定量を知るため」の関数です。\(\theta\)は未知です。
そして、尤度関数はパラメーターが\(\theta\)の時の密度の積で表されます。
$$L(\theta;X)=f(X_{1};\theta)×…×f(X_{n};\theta)$$
パラメーターが\(\theta\)の時の確率を全て掛け合わせた、この尤度関数を最大にする\(\theta\)を採用します。
周辺確率の積で表されるということですね。
$$L(\theta;x)=\prod_{i=0}^Nf(x_{i})$$
上のように表すことができます。
総積なので、総和の\(\sum\)とは異なります。
このままでは解けないので、対数をとり、対数尤度関数を作ります。
$$logL(\theta;x_{i})=\sum_{i=0}^Nlogf(x_{i}|\theta)$$
便利なことに、対数をとると、掛け算は足し算の形になります。ここで、最大化問題を解きます。
\(\theta\)に関して微分を行い、ゼロになる時の\(\theta\)が最尤推定量になります。
MLでMax Likelihood(最尤推定量)です。
$$\frac{d}{d\theta}l(\theta;x)=0,\hat{\theta}^{ML}$$
最尤推定量の特徴
最尤推定とは、「我々が観測している現実の標本は、確率が最大のものが実現している」という考えからきています。
最尤推定量は以下のような特徴があります。
①一致性をもつ。
nが十分に大きいとき、推定量が真の値と同値になるということですね。
②漸近正規性を持つ。
nが十分に大きいとき、最尤推定量は正規分布で近似できます。
サンプル数の平方根と残差の積が正規分布に従うという性質があるということですね。
下図の通りです。
$$\sqrt{n}(\hat{\theta}^{ML}-\theta)\approx N(0,\frac{1}{I(\theta)})$$
\(I(\theta)\)はフィッシャー情報量と呼びます。
かなり細かいですが、フィッシャー情報量は以下の式で与えられます。
確率密度に対数をとり、微分したものを二乗した期待値です。
$$I(θ)=E[(\frac{d}{dθ}logf(X_{1};θ))^2]$$
また、細かいですが、以下の不等式をクラメール・ラオの不等式と呼びます。
つまりフィッシャー情報量が大きいほど推定量の誤差の期待値の下限は小さくなります。
$$E[\hat{\theta}-\theta]≧\frac{1}{nI(\theta)}$$
詳しくは以下のコンテンツからご覧ください。
③不変性を持つ
よく聞く不偏性ではありません。
この不変性は、「関数自体g(θ)の最尤推定量が、θの最尤推定量を代入した形で求められる」ということです。
非常に便利な性質です。
$$g(\theta)^{ML}=g(\theta^{ML})$$
最尤法は、情報量基準の計算で使われています。
モデル選択にどう使われているのか知りたい方は以下のコンテンツをご覧ください。
最尤推定量の欠点
最尤推定量の欠点は以下の3点が挙げられます。
①計算量が膨大になる場合が多い。
密度関数を最大化するので、数理最適化の式を解く必要があります。
それほど問題にはなりません。
②外れ値に弱い
外れ値に対して適切な処理をしていない場合、大きく影響を受けます。
③分散が過小評価される
サンプル数が大きくなれば、この問題は軽減されていきます。
ただ、この欠点が過学習(overfitting)を生む原因であります。
$$E[\sigma_{ML}]=\frac{N-1}{N} \sigma^2$$
最尤推定量には、不偏性(推定量の期待値が真の値になる)がありませんが、データ量を増やせば、一致性や漸近性などのそれに近い状態を得られるため、問題視されることは少ないです。
不偏性については以下のコンテンツで学習してください。
例題(1)
\(X_{i} (i=1〜n)\) がベルヌーイ分布 \(Ber(p)\) に従う時、パラメーター\(p\)を最尤推定しましょう。
【解説】
ベルヌーイ分布の確率分布関数は以下の通りです。
$$f(x|p)=p^{x}(1-p)^{1-x}$$
では、同時確率をとって尤度関数を作りましょう。
$$L(p;x)=\prod_{i=0}^{N}p^{x_{i}}(1-p)^{1-x_{i}}$$
積は、指数で言うと和になりますので、比較的計算は楽かもしれません。
$$L(p;x)=p^{n\overline{x}}(1-p)^{n(1-\overline{x})}$$
平均値にサンプル数nをかけたもので表しています。
では、対数尤度関数を作りましょう。
$$l(p;x)=n\overline{x}log(p)+n(1-\overline{x})log(1-p)$$
このように和の形になりました。
次は、pに関して微分してイコール0を取ります。
\(log\)の微分を思い出しましょう。
分数になります。
$$\frac{n\overline{x}}{p}+n(1-\overline{x})\frac{1}{1-p}=0$$
この方程式の解である、\(\theta\)が最尤推定量になります。
計算は省きますが、xの標本平均になります
$$\hat{p}^{ML}=\overline{x}$$
例題(2)
\(X_{i} (i=1〜n)\) がポアソン分布 Po(\lambda) に従う時、パラメーター\(\lambda\)を最尤推定しましょう。
【解説】
ポアソン分布についての復習したい方は、以下のコンテンツをご覧ください。
まずは、ポアソン分布の確率分布を見てみましょう。
$$f(x|\lambda)=\frac{\lambda^x}{x!}e^{-\lambda}$$
\(\lambda\)が生起率でした。
では肝心の尤度関数を求めてみましょう。
$$L(x|\lambda)=\prod_{i=0}^{N}\frac{\lambda^{x_{i}}}{x_{i}!}e^{-\lambda}$$
では対数尤度関数を作ります。
対数をとると、割り算は引き算になります。
$$l(λ,x)=(\sum_{i=0}^{N}x_{i})logλ-log(x_{1}!…x_{n}!)-n\lambda$$
第二項に厄介そうな数式がありますが、これは後で\(\lambda\)に関して微分した時に0になるので問題ありません。
では、λに関する最大化問題を解きます。
$$\frac{\partial l(\lambda;x)}{\partial \lambda}=(\sum_{i=0}^{N}x_{i})\frac{1}{\lambda}-n=0$$
求める推定量は、\(\lambda\)です。
\(\lambda\)についての方程式を解くと以下のようになります。
$$\hat{\lambda}^{ML}=\overline{x}$$
結局こちらも標本平均でした。
補論|尤度とベイズ統計の関係
これまでの議論で、尤度はあるデータが与えられた条件下で、パラメータの特定の値がどれほど適合するかを表す指標だということがわかりましたね。
この尤度の性質を使って「事前確率を更新する」のがベイズ統計の基本となります。
高校数学でも見たことがあるかもしれませんが、ベイズの定理をまず確認しましょう。
$$P(\theta|X) = \frac{P(X|\theta) * P(\theta)}{P(X)}$$
\(P(\theta|X)\) : データが与えられた条件下で\(\theta\)が発生する確率(事後確率)
\(P(X|\theta)\) :\(\theta\)が与えられた条件下で Xが発生する確率(尤度)
\(P(\theta)\) :\(\theta\)が発生する確率(事前確率)
\(P(X)\) :データが発生する確率(周辺確率)です。
ベイズの定理は、尤度と事前確率を用いて、データが観察された後のパラメータの確率(事後確率)を更新する方法を提供します。
すなわち、事前確率に尤度を掛け、その結果を周辺確率で割ることで、事後確率を計算することができます。
確率分布に関しても同様の議論ができ、事前分布に尤度をかけても事後分布の分布族が事前分布と一緒になることを「尤度と事前分布が共役な関係にある」と呼びます。
ベイズの定理から考えると、事後分布は事前分布\(w(\theta)\)と尤度$${f(z|\theta)}$$の積に比例します。
ベイズ更新を何度も行う関係で、事前分布の形が複雑だと事後分布の形もどんどん複雑になることがわかります。
そこで、共役な関係があると嬉しいということですね。
$${w'(\theta|z)=\frac{w(\theta)f(z|\theta)}{\int_{\Theta}w(\theta)f(z|\theta)d\Theta} \propto w(\theta)f(z|\theta)}$$
ベイズの定理に関しては、こちらの記事でより平易に説明しております。
最尤法とMAP推定(最大事後確率推定)について
例えばデータが少ない時のように、最尤法だとパラメータが信頼できません。
→そのデータがまれにしか得られないデータかもしれないからですね。
そこで、与えられたデータに基づいて事後分布を最大化するパラメータの値を見つけるアプローチをMAP推定と呼びます。
$$\hat{\theta}_{MAP}=argmax_{\theta}p(\theta|D)=argmax_{\theta}p(D|\theta)p(\theta)$$
上の式で見るとわかりやすいですね。
最尤法だと、あるパラメータが与えられた時にデータが得られる確率(これを尤度と呼びます)\(p(D|\theta)\)が、最大化されます。
さて少し踏み込んだ内容になりますが、一般に考慮すべきパラメータ空間が大きい場合や尤度関数が複雑な場合は周辺確率\(P(X)\)の計算が困難な場合があります。
\(P(X) = \int P(X|\theta)P(\theta) d\theta\) (連続パラメータの場合 )
\( P(X) = \sum P(X|\theta)P(\theta)\) (離散パラメータの場合)
そのような場合には一般的にMCMC法(マルコフ連鎖モンテカルロ法)などの事後分布を近似した分布からサンプリングを行う方法などが使われます。

