【完全版】二項分布をわかりやすく説明|統計学
こんにちは、青の統計学です。
今回は、離散確率分布の一つ二項分布をテーマに解説していきます。
母比率の検定や正規近似、ベルヌーイの繰り返しverなど、統計学を勉強していると多く目にすることがあると思います。
これを機にしっかり理解していきましょう。
より網羅的に確率分布を勉強したい方はこちらもおすすめです。

二項分布
二項分布を理解するには、まずベルヌーイ分布の理解が必須です。
ベルヌーイ分布は、単一の確率実験において、成功(1)か失敗(0)の2値をとる離散確率分布です。
確率質量関数は、
$$P(X=x) = p^x(1-p)^{1-x}, \qquad x=0,1$$
で表されます。
ここで、pは成功確率です。
ベルヌーイ分布の期待値と分散は、以下のように求められます。
$$\mathbb{E}[X] = p, \qquad \mathbb{V}[X] = p(1-p)$$
一方、二項分布は、この単一のベルヌーイ試行を独立に繰り返した場合の、成功回数の確率分布を表します。
つまり、\(n\)回のベルヌーイ試行において、成功回数が\(X\)である確率を表す分布です。
もう少し厳密にいうと、\(Y_1,..,Y_n\)が独立に、同一の\(p\in(0,1)\)で指定されるベルヌーイ分布にしたがっている時の、\(X=\sum Y_i\)の従う分を二項分布\(B(n,p)\)と呼びます。
確率質量関数は以下になります。
$${P(X=x)={}_nC_xp^x(1-p)^{n-x}}$$
よくコイン投げが例に挙げられますが、当然2項分布はコイン投げ以外にも使い道はあります。
例えば内閣支持率調査の場合でも2項分布があてはまります。
\(n\) 人に調査を行うとし、\(n\) 人の中で内閣 を支持する人の数を \(X\)とします。
また日本人有権者全体を無限母集団とみなすと、この調査は \(n\) 回の ベルヌーイ試行列であり、 \(p\) を日本人有権者全体での内閣支持率とすれば、確率変数\(X\) は2項分布 \(B(n, p)\) に 従います。
では、期待値と分散を考えてみましょう。
ベルヌーイ分布と同様に考えやすく、直感的にわかります。
二項分布の期待値と分散の導出
期待値
二項分布の期待値を求めます。
$$\begin{align*}E(X) &= \sum_{x=0}^{n} x \cdot P(X=x) \\&= \sum_{x=0}^{n} x \cdot {}_nC_x p^x (1-p)^{n-x}\end{align*}$$
高校数学で習ったと思いますが、二項係数\({}_nC_x\)は\(n\)個から\(x\)個選ぶ組み合わせの数を表します。
\(x\)を固定すると、残りの\(n-x\)個から選ぶ組み合わせの数は\(1\)通りしかありませんよね。
そのため、
$${{}_nC_x p^x (1-p)^{n-x} = {}_nC_x p^x \cdot 1 \cdot (1-p)^{n-x}}$$
$${ {}_nC_x p^x = \frac{n!}{(n-x)!x!}p^x}$$
と変形できます。
これを代入すると、
$$
\begin{align*}
E(X) &=x \sum_{x=0}^{n} \left( \frac{n!}{(n-x)!x!} p^x \cdot 1 \cdot (1-p)^{n-x} \right) \\
&= np \sum_{x=0}^{n} \frac{(n-1)!}{(n-x)!(x-1)!}p^{x-1}(1-p)^{n-x} \\
&= np \cdot 1 \end{align*}
$$
ポイントとしては、\(x!=x(x-1)!\)と分けて、実現値の部分は消してしまい、\((x-1)!\)に合わせて、二項係数を作り替えた結果\(n,p\)の二つがサメンションの外に出せるという点ですね。
よって二項分布の期待値は、\(E(X) = np\)となります。
分散
分散は、\(V(X) = E(X^2) – E(X)^2\)から求められます。
この公式自体は理屈と一緒に覚えたいですね。
まず、期待値の二乗である\(E(X^2)\)を求めましょう。
$$\begin{align*}E(X^2) &= \sum_{x=0}^{n} x^2 \cdot P(X=x) \\&= \sum_{x=0}^{n} x(x-1) \cdot P(X=x) + \sum_{x=0}^{n} x \cdot P(X=x) \\&= \sum_{x=0}^{n} x(x-1) \cdot {}_nC_x p^x (1-p)^{n-x} + np \\&= n(n-1)p^2 + np \end{align*}$$
計算のテクニックとしては、期待値と同じで実現値\(x^2\)の扱い方になります。
\(x^2=x(x-1)+x\)と変換して、二項係数で分母をキャンセルできるようにしています。
さて、既に求めた\(E(X)=np\)を使うと、
$$
\begin{align*}
V(X) &= E(X^2) – E(X)^2 \\
&= n(n-1)p^2 +np- (np)^2 \\
&= n^2p^2+np^2+np – n^2p^2 \\
&= np(1-p)
\end{align*}
$$
となります。
では、確率質量関数の図を見てみましょう。
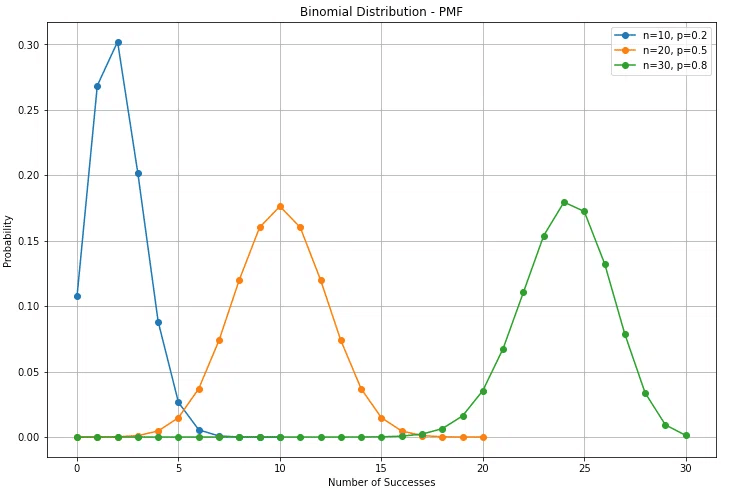

分布の形状としては、特に $${p}$$が大きくなると、成功回数の分布は右に移動し、より分散します
二項分布の正規近似について
さて、二項分布の特徴の一つに「正規分布に近似できる」というものがあります。
この特徴を使って、母比率の検定における検定統計量は標準正規分布に従うこととみなし、検定が行えたりします。
詳しくみていきましょう。
二項分布が正規分布に近似できる理由は、中心極限定理に基づいています。
中心極限定理は、独立で同一の分布に従う確率変数の和が、一定の条件のもとで正規分布に収束するという定理です。
再度、二項分布の成り立ちからみましょう。
二項分布 \(B(n, p)\) は、\(n\) 回の独立なベルヌーイ試行の結果として得られる成功の回数を表します。
各試行では、確率 \(p\) で成功し、確率 \(1-p\)で失敗します。
二項確率変数\(X\)は、\(n\)個の独立なベルヌーイ確率変数\(X_1, X_2, \dots, X_n\)の和として表すことができます。
$${X = \sum_{i=1}^{n} X_i}$$
ここで、\(X_i\) は \(i\) 番目の試行の結果を表し、成功なら\(1\)、失敗なら\(0\)の値をとります。
中心極限定理により、$${n}$$ が十分に大きく、\(p\) が\(0\)や\(1\)に近すぎない場合、二項分布 \(B(n, p)\) は正規分布 \(N(np, np(1-p))\) に近似することができます。
$${\frac{X – np}{\sqrt{np(1-p)}} \stackrel{d}{\to} N(0, 1) \text{ as } n \to \infty}$$
直感的には、\(n\) が大きくなるにつれて、二項分布の確率質量関数が左右対称な釣り鐘型の形状に近づいていきます。
また、\(p\) が\(0\)や\(1\)に近すぎない場合、二項分布の裾が正規分布の裾に近づくのです。
中心極限定理をしっかり理解したい方はこちらの記事もどうぞ
二項分布とベータ分布の共役関係について
正規分布に続いて、他の分布とのどんな関係があるのかを深掘ります。
ベイズ更新の文脈で考えられる、共役関係についてです。
二項分布の共役事前分布は、ベータ分布という分布になります。
共役に関して基礎的に理解したい方は、こちらの記事をご覧ください。




さて、共役事前分布となるのは、事前分布と尤度関数の分布の形が同じになるためでしたね。
まず、二項分布の尤度関数は、観測されたデータが与えられた条件下でのパラメータ\(\theta\)の尤度を評価します。
\(n\)回の試行で\(k\)回成功した場合の尤度は次のように表されます
$${L(\theta)=\begin{pmatrix}n \\k \\\end{pmatrix}\theta^k(1-\theta)^{n-k}}$$
事前分布がベータ分布 \(Beta(\alpha,\beta)\) である場合、尤度関数と事前分布の積は以下のようになります
$${Posterior\propto \theta^{\alpha-1}(1-\theta)^{\beta-1}×\theta^k(1-\theta)^{n-k}=\theta^{\alpha+k-1}(1-\theta)^{\beta+n-k-1}}$$
同じ形ですね!!
新しいベータ分布 \(Beta(α+k,β+n−k)\)の確率密度関数の形式と一致します。
→つまり、事後分布もベータ分布に従います。
二項分布の共役事前分布がベータ分布である理由は、二項分布の尤度関数とベータ分布の確率密度関数が掛け合わされた結果、事後分布が同じベータ分布の形式を保つためとわかりました。この辺りは統計検定準一級でよく出る話なので、覚えておきましょう。

