【完全ガイド】MCMC法についてわかりやすく解説|ベイズ推定
MCMC法|Markov Chain Monte Carlo法
今回は、ベイズ理論を使ったパラメータ推定手法であるMCMC法(Markov Chain Monte Carlo法 マルコフ連鎖モンテカルロ法)について解説いたします。
ベイズの定理から丁寧に解説していきますので、ベイズの考え方に馴染みがなくてもOKです。
ベイズの定理
ベイズの定理について、具体例を元に解説した、より平易なコンテンツは以下になります。
さて、ベイズ推量の世界では、全ての確率は主観的な確率 (subjective probability) だとされています。
普通、確率というのは対象の不確かさを示す量とされますが、ベイズ推量では不確かさはその対象を観測する人の知識にあると考えており、それを主観確率と呼んでいます。
では、事前確率と事後確率について説明します。
ベイズの定理で使う事前確率 ${P(X)}$ とは、観測者が観測以前に持っている主観確率を確率分布関数で表現したものです。
ちなみに、事前分布に無情報一様分布を設定すると、事後分布と尤度関数が一致するので、MAP推定量は最尤推定量と一致します。
この辺りは頻度論と整合性があって素敵ですね。
一方、事後確率はなんでしょうか？
例えば、観測した結果を \(D\) とします。
観測結果 \(D\) によって、確率変数 \(X\) に関する主観確率が変化します。
観測結果 \(D\) のもとで確率変数 \(X\) に関する主観確率を \(P(X|D)\) と書き、事後確率 (posterior) と呼んでいます。
この事後確率分布を求めるのがベイズ推量の目的です。
事後分布の解釈
事後分布は、データを観測した後に、パラメータがどのような値をとる可能性が高いかを示す確率分布です。この分布から、パラメータの平均値、分散、信頼区間などを計算することができます。
尤度|lilelihoodとは
ベイズ統計では、尤度という概念が必要です。
尤度はいわばモデル自体の仕様であり、モデルのパラメータ値が${\theta}$だと仮定した場合のデータ値の確率を指定する分布です。
ベイズ分析が実施された後、パラメータ ${\theta}$について推論と推定が行われます。
詳しく知りたい方は以下のコンテンツをご覧ください。
確率変数 X(以後パラメータと呼びます) の元では、観測結果 \(D\) が確率 \(P(D|X)\) に従って生成されるはずであることが分かっていたとします。
\(P(D|X)\) を \(D\) が観測された時の \(X\) の尤度 (likelihood) と呼びます。
さて、これまで紹介した事前確率 \(P(X)\)、事後確率 \(P(X|D)\)、尤度 \(P(D|X)\) の間には以下の関係が成り立ちます。
$${P(X|D)=\frac{P(D|X)P(X)}{\int P(D|X)P(X)}}$$
これをベイズの定理と呼びます。
また分母の値を特に エビデンス(evidence) と呼びます。
ベイズ統計では、このベイズの定理を用いて、データから直接パラメータの確率分布（事後分布）を推定します。
従来の頻度論統計学では、パラメータを固定の値として推定するのに対し、ベイズ統計ではパラメータ自体が確率変数であると捉える点が大きな特徴です。
次元の呪い|なぜモンテカルロ法だと推定が難しいか
さて、複数のパラメータを持つモデルでは、それらのパラメータの同時確率分布を共同事後分布と呼びます。
この分布は、パラメータ間の複雑な関係を表しており、パラメータの数が増えるにつれて、その形状はますます複雑になります。
まずモンテカルロ法というランダムなサンプリング法を考えてみます。
統計検定準1級でも、正方形の中に90度の扇形を入れて、ランダムにサンプリングして、円の面積を求めていくという問題がありました。
このように、乱数を用いた試行を繰り返すことで近似解を求める手法で、確率論的な事象についての推定値を得る場合を特に「モンテカルロシミュレーション」と呼びます
モンテカルロ法｜提案分布と採択について
モンテカルロ積分では、まず、積分したい関数を覆うような提案分布を考えます。
この提案分布からランダムにサンプルを生成し、そのサンプルが積分範囲内にあるかどうかを判定します。
範囲内にあるサンプルは採択され、そうでない場合は棄却されます。
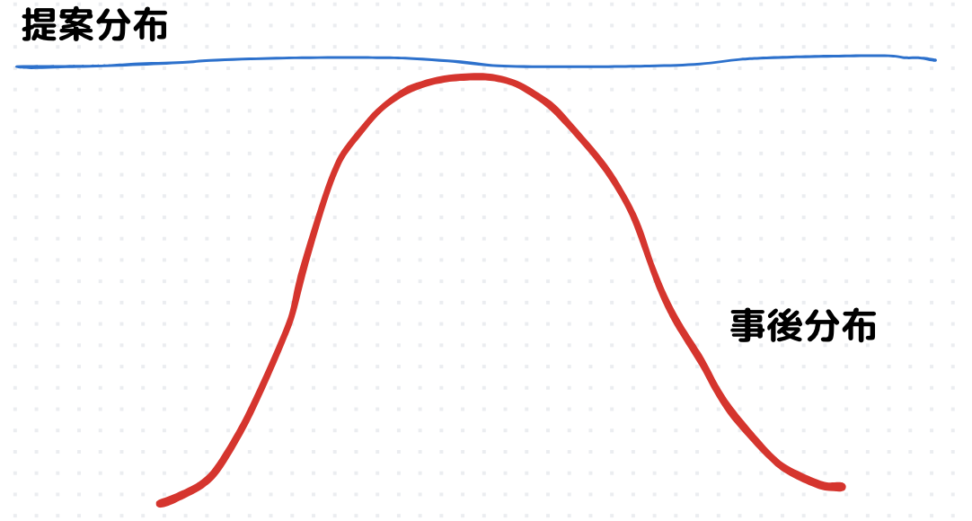
提案分布を一様分布\(U(0,1)\)として、提案分布から乱数\(X〜U(0,1)\)を発生させていきます。
この分布からランダムにサンプルを生成し、そのサンプルを用いて積分を近似します。
$${\theta=\int_{0}^{1}g(x)dx}$$
提案分布からN個のサンプル${x₁, x₂, …, xₙ}$を生成した後、各サンプル${xᵢ}$に対して、関数${g(xᵢ)}$の値を計算する、ということですね。
モンテカルロ積分は事後確率分布 \(P(X|D)\) からサンプル \(X\) を取り出すことで期待値\(E[g(X)]\)を近似値的に評価していきます。
大数の弱法則により、サンプリング回数が無限大になると、\(θ\)に確率収束します。
$$E[g(X)]=\hat{θ}=\frac{1}{n} \int_{0}^{1}g(X_i)dx$$
ランダムサンプルを生成して、それらの平均を取ることで積分値を近似します。
ここで注意して欲しいのが、モンテカルロ法は、関数の形を完全に把握するのではなく、その関数に関するある種の統計量（今回平均値）を近似的に求めるための手法という点です。
で、なんで直接事後分布から期待値を計算できないかでいうと積分計算が大変だからです。
思い出していただきたいのが、期待値を求めるためには、事後分布とパラメータの積を全パラメータ空間で積分する必要があるということです。この積分が解析的に解けない場合がほとんどです。
ただし、モンテカルロ法にも問題点があります。
1回ごとのサンプリングが独立なので、高次元だと殆ど棄却されてしまうのです。
高次元になると、提案分布に対して採択される的が小さいイメージを持っていただけると良いと思います。
高次元空間では、分布が疎になることが多く、効率的なサンプリングが困難になる可能性があるということですね。
これを次元の呪いと呼びます。
多項式曲線のフィッティングの問題ですね、係数の数が冪乗に増加していき、高次元になると幾何的な直感が当たらないです。
次元の呪い
高次元空間では、単純なモンテカルロ積分は効率が悪くなります。これは、高次元空間では、関数の値が非常に小さい領域が大部分を占めるため、ランダムにサンプリングしても、関数の値が大きな領域をほとんどサンプリングできないからです。この現象を次元の呪いと呼びます。
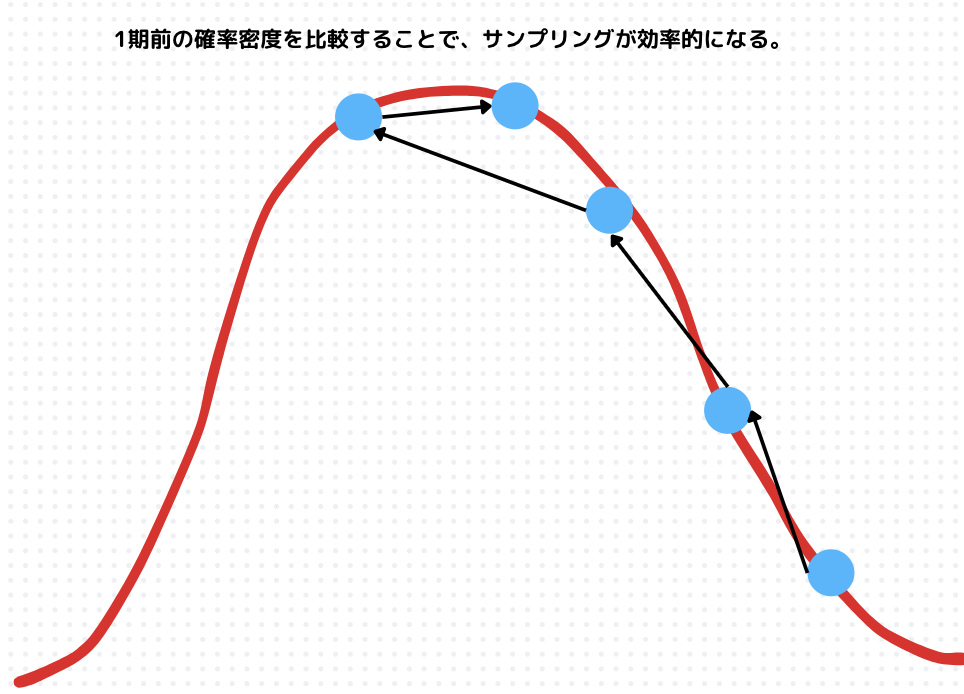
では効率よくサンプリングするには、一期前のサンプリングを使えば良いのではという発想が自然と生まれるはずです。
これが、マルコフ連鎖モンテカルロ法の着想です。
マルコフ連鎖
では、事後確率分布をどう推定すれば良いでしょうか？
次にマルコフ連鎖という考え方を使ってサンプリングをします。
時刻 \(t,t ≥ 0\) において、系列の現在の状態 \(X_t\) だけに依存する分布 \(P(X_{t+1}|X_t)\) から次の状態 \(X_{t+1}\)をサンプルして、ランダムなパラメータの列 \({X_0, X_1, X_2, . . . }\) を生成することを考えます。
つまり、\(X_t\) を決めると次の状態 \(X_{t+1}\) はそれより過去の系列 \({X_0, X_1, . . . ,X_{t−1}}\) には依存しないとします。
現在の状態（今日の天気）が次の状態（明日の天気）を予測する上での必要な情報となるような確率的な過程（というか現在の天気以前の天気はどうでもいい）です。例えば、雨が降った日は、翌日も雨が降りやすいというように、状態は時間とともに推移していきますね。
$${P(X_{n+1}=j|X_{n},X_{n-1},…,X_0)=P(X_{n+1},X_n=i)}$$
このような確率過程を、状態空間 S 上のマルコフ連鎖と呼びます。
ここでは系列は時間的に一様で\(t\) に依らないとすると、上のマルコフ連鎖は単一の定常分布 (stationary distribution) に収束することが知られています。
確率分布 ${\pi}$ がマルコフ連鎖の定常分布であるとは、任意の状態 ${i,j∈S}$ に対して以下の条件が成り立つときをいいます。
$${\pi(j)=\sum_{i\in S}\pi(i)P(X_{t+1}=j)|X_t=i}$$
さて、この定常分布を \(π(X)\) とすると、定常分布\(\pi(X)\) が正確に事後確率分布 \(P(X|D)\) に近づくような操作を行うのが MCMC 法の目的です。
収束とは
状態遷移を繰り返していくと、最終的には、状態が事後分布の高い確率密度を持つ領域に集中するようになります。つまり、マルコフ連鎖の状態が、事後分布からサンプリングされた値に近づく。
\(t\) が増加するにつれてサンプル点は定常分布からサンプルされるようになり、初期条件の情報は失われます。
つまり定常分布は初期状態には依らないことになります。
→主観によって設定される事前分布の影響は受けにくい！！！
繰り返しになりますがマルコフ連鎖は、各ステップが前のステップのみに依存する性質を持ち、時間が経つにつれて分布が収束します。あくまで状態が変わるのはマルコフ連鎖という確率過程であって、提案分布ではありません。
提案分布が頻繁に変化すると、マルコフ連鎖が定常分布に収束しにくくなり、計算量も増えそうですね。
これにより、複雑な確率分布からのサンプリングが可能になるというわけです。
どのように事後分布からサンプリングをするか
- 提案分布の設定: 事後分布の形をある程度考慮して、提案分布を設計します。
- マルコフ連鎖の構築: 提案分布に基づいて、マルコフ連鎖を構築します。
- サンプリング: このマルコフ連鎖を繰り返し実行し、状態を遷移させます。
- 定常分布への収束: 十分な回数の繰り返し後、マルコフ連鎖は定常分布に収束します。
- 定常分布からのサンプリング: 定常分布に収束した後、生成されたサンプルは、近似的に事後分布からサンプリングされたものとみなすことができます。
具体的には、MCMCは以下のような流れになります。
①初期値\(X_0\sim p(X_0)\)を決める
②乱数で今の\(X\)から新しい\(X_{new} \sim q(X_{new}|X)\)を探してくる
③尤度の大小関係を調べます。
$${f(X_{new}|D)>f(X|D)}$$
実はこの③のプロセスがアルゴリズムよって違ってきます。例えば、後述するMHだと、新しい状態を提案する際に、提案分布からサンプルを生成しますが、そのサンプルが必ずしも受け入れられるわけではありません。受容確率というものに基づきます。
④真であれば、状態を更新し、偽であればある程度の確率で受容する。
⑤②-④を繰り返す。
ここで$${q(X_{new}|X)}$$は提案分布 (新しい状態(X_{new})を提案する確率分布)です。
上図のように、尤度が高い部分をフラフラとサンプリングしていくようになります。
提案分布と事後分布の関係を設計することで、マルコフ連鎖の定常分布が、目標とする事後分布に一致するようにします
補足｜二次元での説明
MCMC法は、よく山登りや洞窟の中でてっぺんを探すために石を真上に投げる行為、とかに例えられたりします。
ここでは、二次元ではありますが、山登りを例に上の説明を具体的に行います。
初期値の設定: 山のどこかにランダムに点を打ち、その点を(X_0)とします。
新しい点を探す: 現在の点(X)の近くをランダムに探索し、新しい点(X_{new})を見つけます。これは、山を少しだけ移動することを意味します。
新しい点の評価: 新しい点(X_{new})が、現在の点(X)よりも高い位置にあるかどうかを調べます。これは、尤度(f(X|D))を計算することで行います。
- もし(X_{new})の方が高ければ: 新しい点(X_{new})は、より山の頂上（事後分布のピーク）に近い場所にあると考えられるため、そのまま(X_{new})に移動します。
- もし(X_{new})の方が低ければ: 新しい点(X_{new})は、現在の点(X)よりも低い場所にあるため、必ずしも移動するわけではありません。ある確率（受容確率）で(X_{new})に移動し、そうでなければ、元の点(X)にとどまります。この確率は、(X_{new})と(X)の高さの差によって決まります。
繰り返し: ステップ2と3を何度も繰り返します。
詳細釣り合いと遷移核
先ほど、「マルコフ連鎖が定常になる〜」と簡単に説明しましたが、どのような条件を満たせばマルコフ連鎖は定常になるのでしょうか？
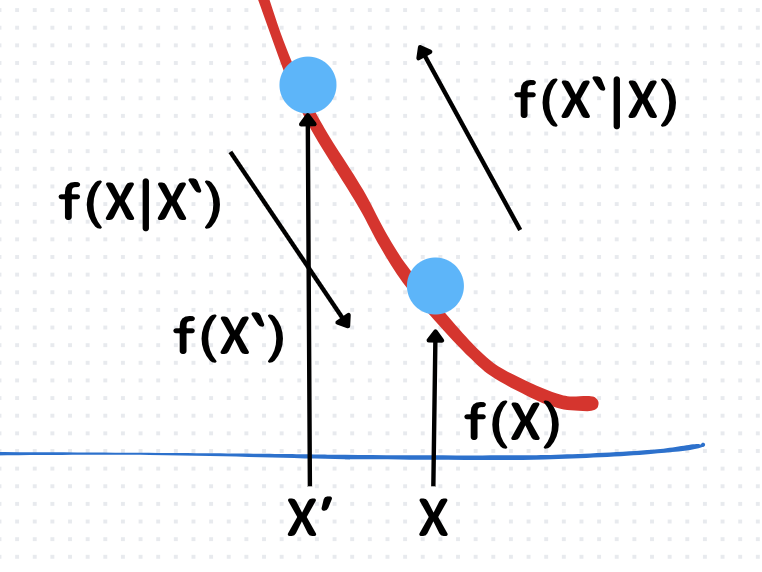
結論から申し上げると、下のように一期前と現在の遷移核と事後分布の積が等しくなる場合です。
$${f(X’|X)f(X’)=f(X|X’)f(X)}$$
\(f(X|X’)\)：遷移核(移りやすさのようなイメージ)
→パラメータ\(X’\)から\(X\)にどれだけ移りやすいか
\(f(X)\)：事後分布(起こりやすさ)
とはいえ、この条件は十分条件なので、マルコフ過程が定常分布に収束するための必須の条件ではないです。
詳細釣り合いの条件
マルコフ連鎖の遷移確率が、ある条件（詳細均衡条件）を満たすように設計されているため、定常分布（マルコフ連鎖が十分な時間を経た後に収束する分布）が、事後分布と一致するようにすることができる。
メトロポリス・ヘイスティングアルゴリズム|Metropolis-Hastings algorism
上で説明したような、詳細釣り合いを満たすための遷移核のバリエーションはいくつかあります。
ここでは、MHアルゴリズムをご紹介します。
上の遷移核の議論で思った方も多いと思いますが、「事後分布の形が複雑で直接サンプリングできないという話だったのに、遷移核がわかっているのはなぜ？」となるはずです。
その通りで、遷移核\(f(X’|X)\)を見つけるのは簡単ではなく、遷移核に従うような乱数を発生させることも同様に難しいです。
なので、サンプリングが簡単な遷移核\(q(X’|X)\)で代用することがMHのスタートです。
→これを提案分布と呼びます。
ただ、提案分布は真の遷移核ではないので、詳細釣り合いは満たされないので下のような補正係数\(r\)を導入します。
この\(r\)について解けば良いことになります。
$$rq(X’|X)f(X’)=q(X|X’)f(X)$$
そして、\(q(X’|X)f(X’)>q(X|X’)f(X)\)ならば、\(r\)を使って確率的に補正をしていきます。
一方で、上の条件式が偽であるならば、新しいパラメータを受け入れた方が詳細釣り合いを満たすので受容します。
この試行を繰り返していきます。
ちなみに提案分布が\(q(X’|X)=q(X|X’)\)のようなランダムウォーク(つまり、パラメータの移りやすさが1期前と同じ)であるならば、補正係数\(r\)は一期前と現在の事後分布の比になることがわかります。
何が嬉しいかというと、計算量が少なくなるのに加えて、探索空間の広範囲カバーが挙げられます。
というのも、ランダムウォークは事後分布の異なる領域を探索するのに役立ちます。
局所的な最大値に囚われるリスクを軽減し、より全体的な分布の特徴を捉えることができます。
