【ベイズの定理】事後分布から推定量を導く方法について|python
今回はベイズ統計学の基礎の基礎を解説いたします。
ベイズの定理の理解の後、ベイズ更新のやり方を学んでいく形にします。
ベイズ統計学
ベイズ統計とは？
ベイズ統計学は、経験を数値化し、数学的に扱う手法です。この手法はベイズの定理に基づいており、過去のデータをもとに現時点の考えを更新することが特徴です。この考え方をベイズ更新と呼びます。
ベイズ更新の考え方
ベイズ更新は、統計的な推測方法の中でも特に経験に基づいて考えを修正していくプロセスです。これにより、現時点での事象に対する理解を深め、次の行動に反映させることができます。
ベイズ更新の例：日常生活での応用
例えば、事前確率として、道の角から人が飛び出してくる確率を/(0.5/)と仮定します。
しかし、ある朝、実際にその状況が発生し、衝突してしまったとします。
この経験から、「朝の通勤時間には人が飛び出してくる確率が高い」と考え、翌日はより注意して歩くようになるでしょう。
このように、ベイズ統計学は日常生活の様々な場面で自然に用いられているのです。
ベイズ統計学の応用例
ベイズ統計学は、日常的な意思決定だけでなく、ビジネスや科学的な推測にも広く応用されています。
例えば、医療分野では新薬の効果を判断する際にベイズ統計が用いられることがあり、マーケティングでは顧客行動の予測にも利用されています。
ベイズの定理
では、ここでベイズの定理について解説します。
その前に、事前分布と事後分布について理解をする必要があります。
事前分布：データを観測する前のパラメータの分布
事後分布：データを観測した後のパラメータの分布
尤度に関しては、以下をご覧ください。
では、例を見てみましょう。
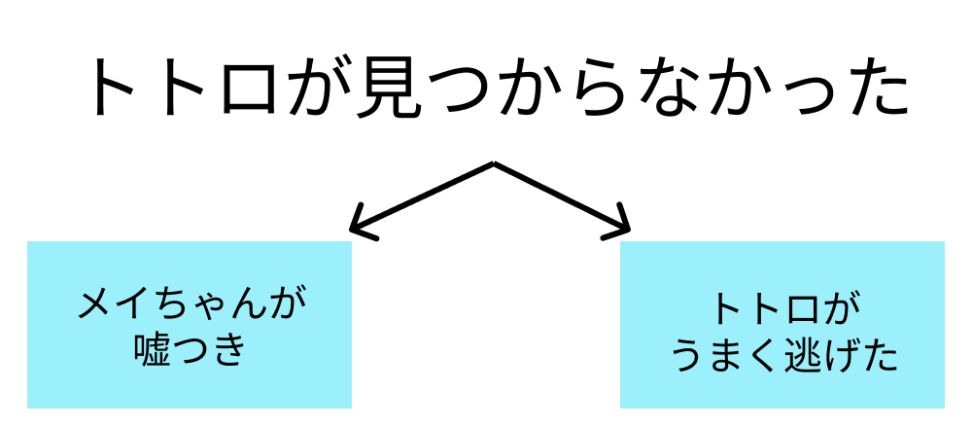
例：「トトロいたもん！」 メイちゃんは、どうやらトトロをみたらしいです。 しかし、森の中を探しても全然見つかりませんでした。 この時、メイちゃんが嘘つきである確率をベイズの定理を使って求めてください。 情報： メイちゃんが嘘つきの場合、「実際にトトロが居てもいなくても」、「トトロいたもん！」と出力します。 メイちゃんは普段嘘をつく方ではないので、メイちゃんが嘘つきである事前確率は0.1です。 メイちゃんが正直者の時に、トトロが見つかってしまう確率を0.8とします。 一方、メイちゃんが嘘つきの時にトトロが見つかってしまう確率は0.3とします。
今回求めるのは、以下の条件付き確率です。
$$P(嘘つき｜観測できない)$$
今回の確率は、ベイズの定理を使って以下のように求めることができます。
$${p(嘘つき|発見されない)=\frac{p(嘘つき)×p(発見されない|嘘つき)}{p(発見されない)}}$$
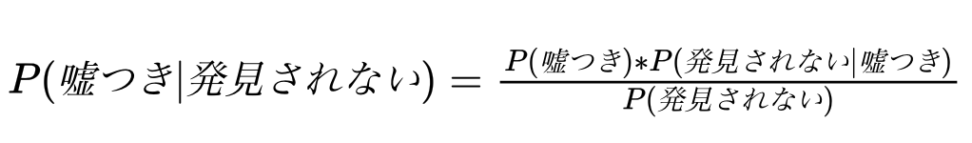
分母：\(P(観測できない) = P(観測できない | 嘘つき)*P(嘘つき) + P(観測できない | 正直者)*P(正直者) = 0.1 * 0.7 + 0.9 * 0.2 = 0.25\)
分子：\(P(嘘つき)*P(観測できない | 嘘つき) = 0.1 * 0.7 = 0.07 \)
よって、求める確率は\(0.28\)です。
ベイズの定理は一般的には、以下のような式です。
求めたい条件付き確率は、逆の条件付き確率を使えば求められる、ことになります。
$$P(A|B)={\frac{P(A)P(B|A)}{P(B)}}$$
「逆」というのは、AとBを原因と結果に分けた時にわかりやすくなると思います。
以下のように、「原因がわかれば結果がわかる」確率を、「結果がわかれば原因がわかる」確率に加工できます。
今回の例でいえば、「トトロが居なかった」という結果から、
1「メイちゃんは正直者だが、トトロが逃げた」
2「メイちゃんが嘘つきだった」
という原因の確率を求める、ということになります。
$$P(原因|結果)={\frac{尤度*P(結果|原因)}{P(結果)}}$$
ただ、P(結果)は往々にして計算が大変な場合があります。
今回のように単純な例を除き、事後分布の計算には「マルコフ連鎖モンテカルロ法(MCMC法)」という、「尤度と事前分布の積だけで事後分布を近似させる」という手法がよく使われます。
【完全ガイド】MCMC法についてわかりやすく解説|ベイズ推定
ベイズの定理における、尤度と事前分布と事後分布の関係は以下の通りです。
尤度という「メイちゃんが嘘つきの時に、観測できかった確率」を使って、事前分布(確率)という「嘘つきの確率」が
事後分布(確率)という「観測できなかったときに、嘘つきの確率」に変わりました。
$$事後分布= \frac{事前分布*尤度}{P(結果)}$$
さて、トトロを観測できなかった時にメイちゃんが嘘つきの確率が0.1→0.28とわかりました。
‥しっくりこないでしょうか。
それは、「トトロが逃げる確率」や「メイちゃんが嘘つきの事前確率」を決めうちで設定したから、それを元にした確率が微妙に感じられるのは最もでしょう。
しかし、ベイズ統計学が試行を繰り返していくことで真価を発揮します。
次のベイズ更新で見ていきましょう。
ベイズ更新
では、もう一度メイちゃんが「トトロいたもん！」と言ってきましたが、どれだけ探してもトトロを観測できませんでした。 この時の、メイちゃんが嘘つきの確率を求めてみましょう。 ただし、先ほどの事後確率の情報を使います。 メイちゃんが嘘つきの確率は0.1から0.28にベイズ更新されています。
この時求める確率は以下のようになります。
$$P(観測されない|嘘つき)= \frac{0.28*0.7}{0.28*0.7+0.72*0.2}$$
これを計算すると、0.576になります。
メイちゃんが嘘つきである確率が、0.1→0.28→0.58となりました。
何回も「トトロいたもん！」と言われても、実際にトトロを観測できないときは、メイちゃんが嘘つきである可能性がどんどん高まることになります。
このようにベイズ統計学は、試行結果を繰り返し使って確率を確からしいものに近づける考え方になります。
より一般化すると
例えば、観測した結果を \(D\) とします。
観測結果 \(D\) によって、確率変数 \(X\) に関する主観確率が変化します。
観測結果 \(D\) のもとで確率変数 \(X\) に関する主観確率を \(Pr(X|D)\) と書き、事後確率 (posterior) と呼んでいます。
この事後確率分布を求めるのがベイズ推量の目的です。
確率変数 X(以後パラメータと呼びます) の元では、観測結果 \(D\) が確率 \(Pr(D|X)\) に従って生成されるはずであることが分かっていたとします。
\(Pr(D|X)\) を \(D\) が観測された時の \(X\) の尤度 (likelihood) と呼びます。
さて、これまで紹介した事前確率 \(Pr(X)\)、事後確率 \(Pr(X|D)\)、尤度 \(Pr(D|X)\) の間には以下の関係が成り立ちます。
$$P(X|D)=\frac{Pr(D|X)Pr(X)}{\int Pr(D|X)Pr(X)}$$
CODE
ここでは簡単なベイズ更新のコードを紹介します。
まず事前分布として一様分布が仮定されています。
import pymc3 as pm
# 事前分布
with pm.Model() as model:
p = pm.Uniform('p', 0, 1)
# 観測データ
data = [1, 0, 0, 1, 1, 0, 1, 0, 1, 1]
# 事後分布
with model:
likelihood = pm.Bernoulli('likelihood', p, observed=data)
trace = pm.sample()dataというリスト型の変数に観測データを入れています。
観測データが0か1のベルヌーイ試行に従うものとしています。
また、確率pに対して一様分布を事前分布としています。事後分布は、pm.sample()を使ってサンプリングすることで求めることができます。
発展：共役事前分布について
先ほどのベイズの定理で事後分布を更新していくプロセスですが、事後分布が必ずしも解析的に扱いやすい確率分布ではないことがあります。
ただ、ある事前分布に対して、尤度関数の形を保ちつつ事後分布を計算しやすくする事前分布があり、それを自然共役事前分布と呼びます。
例えば、以下のようなベルヌーイ分布の尤度関数に対して
$$p(x|θ)=θ^x(1-\theta)^{1-x}$$
以下のようなβ分布が自然共役事前分布となります。
$$p(\theta)=θ^{\alpha-1}(1-\theta)^{\beta-1}$$
発展：MAP推定（最大事後確率推定）について
これは例えばデータが少ない時のように、最尤法だとパラメータが信頼できません。
→そのデータがまれにしか得られないデータかもしれないからですね。
そこで、与えられたデータに基づいて事後分布を最大化するパラメータの値を見つけるアプローチをMAP推定と呼びます。
$$\hat{\theta}_{MAP}=argmax_{\theta}p(\theta|D)=argmax_{\theta}p(D|\theta)p(\theta)$$
上の式で見るとわかりやすいですね。
最尤法だと、あるパラメータが与えられた時にデータが得られる確率（これを尤度と呼びます）\(p(D|\theta)\)が、最大化されます。
補足：頻度論統計学との違い
一般的な「統計学」と呼ばれる学問は、「頻度論的な考え」に基づいています。
ここでは、頻度論統計学とベイズ統計学の違いをざっくり解説します。
頻度論：関心のあるパラメータは未知の定数として扱う
ベイズ統計学：関心のあるパラメータは確率変数として扱う
ベイズ統計の大きな特徴は、「正真正銘の事前分布(事前確率)は、主観で決まる」ということです。
この点は、俗にいう頻度論者に嫌われる点です。試行を重ねるごとに、事前分布は客観的な情報を反映して信頼性を増してはいくものの、最初の事前確率は「決め打ち」なのです。
