F検定とは？F分布も含めてわかりやすく解説｜分散分析

1. F検定の概要とその重要性

1.1 F検定とは？

F検定は、2つ以上の母集団の分散の比を統計的に検定するための手法です。具体的には、2群の分散が等しいかどうか、または複数の群間で平均値に有意な差があるか（分散分析：ANOVA）の検定で用いられます。

• 製造業の場合
  複数の生産ラインから抽出したサンプルの分散を比較し、工程間のばらつきを評価。分散に有意な差が認められれば、特定のラインで品質問題が発生している可能性を示唆します。
• 臨床試験の場合
  新薬と既存薬の効果のばらつきをF検定により比較することで、治療効果の安定性や有効性の検証が可能になります。

1.2 F検定の役割

F検定は、単なる分散の比較だけでなく、分散分析（ANOVA）の基礎統計量としても重要で、どちらかというと分散分析でよく使われるイメージです。

これは、多群間の比較において、各群のばらつきを群間変動と群内変動に分解し、その比率（F統計量）により、平均値の差が偶然の産物かどうかを判断します。

2. F分布の理論的背景

2.1 F分布の定義と導出

F分布は、2つの独立なカイ二乗分布から導かれる確率分布です。具体的には、以下の仮定に基づいています。

• 標本 ${X_1, X_2, \ldots, X_{n_1}}$ は、平均 ${\mu_1}$、分散 ${\sigma_1^2}$ の正規分布 ${\mathcal{N}(\mu_1, \sigma_1^2)}$から抽出される。
• 標本 ${Y_1, Y_2, \ldots, Y_{n_2}}$は、平均${\mu_2}$、分散 ${\sigma_2^2}$ の正規分布 ${\mathcal{N}(\mu_2, \sigma_2^2)}$ から抽出される。

各標本から計算される不偏分散 S_1^2と S_2^2 は、それぞれ以下のようなカイ二乗分布に従います。

$${\frac{(n_1 – 1)S_1^2}{\sigma_1^2} \sim \chi^2(n_1 – 1), \quad \frac{(n_2 – 1)S_2^2}{\sigma_2^2} \sim \chi^2(n_2 – 1)}$$

この性質から、分散比

$${F = \frac{S_1^2/\sigma_1^2}{S_2^2/\sigma_2^2} = \frac{S_1^2}{S_2^2} \cdot \frac{\sigma_2^2}{\sigma_1^2}}$$

が、自由度 ${(n_1 – 1,\, n_2 – 1)}$ のF分布、すなわちF(n_1 – 1,\, n_2 – 1)に従うと証明されます。

では、F分布とは実際どんな形なのかというと、こちらになります。

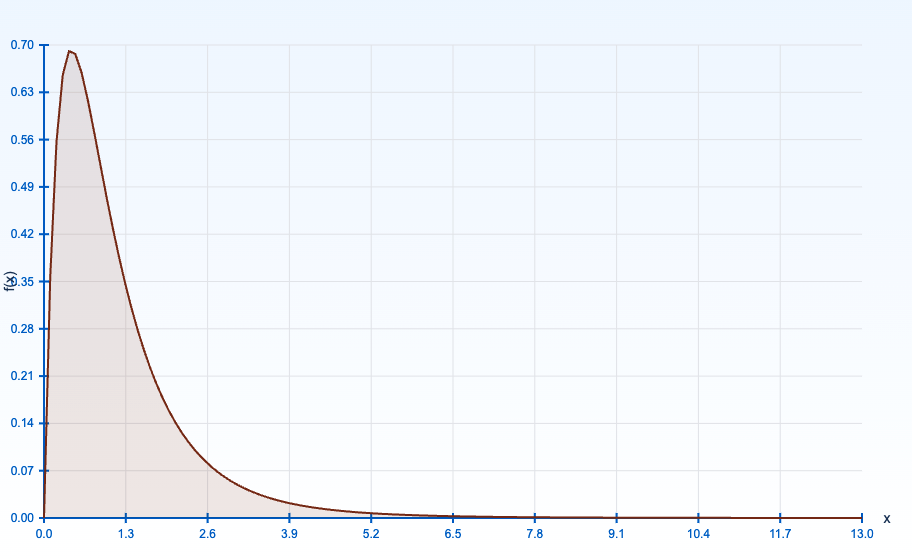
常に正の値をとり、右に歪んだ非対称な形状です。自由度によって形状が変化します。

確率分布シミュレーションは、こちらで簡単にできます。

F分布｜確率分布可視化ツール

2.2 F分布の確率密度関数と性質

確率密度関数を見ていきます。

ただF分布は、t分布やカイ二乗分布と同じように標本に関する分布で、主に分布の形や密度関数を知っておくというよりも、どの検定でどう使われるのか、というところを優先的に理解しておくのが良いです。

F分布の確率密度関数（pdf）は、自由度 ${d_1 = n_1 – 1}$および ${d_2 = n_2 – 1}$ を用いて以下のように表されます。

$${f(x; d_1, d_2) = \frac{\sqrt{\frac{(d_1x)^{d_1}\, d_2^{d_2}}{(d_1x + d_2)^{d_1 + d_2}}}}{x \, \mathrm{B}\left(\frac{d_1}{2}, \frac{d_2}{2}\right)}, \quad x > 0}$$

${\mathrm{B}(\cdot,\cdot)}$ はベータ関数です。

上で見た通り、F分布は、右裾が長く非対称な分布をしており、この性質を利用して有意水準に応じた臨界値（カットオフ値）を設定します。

3. F検定の前提条件と仮定

F検定を正確に実施するためには、いくつかの前提条件を満たす必要があります。これらの条件が整っていないと、検定結果の信頼性が損なわれる可能性があります。

ここでは３つご紹介します。

3.1正規性

実際のデータが正規性から逸脱している場合、検定結果の信頼性が低下するため、事前に正規性検定やデータの前処理（外れ値の除去など）を行う必要があります。

実データだと対数変換などの前処理が事前に必要なケースが多いですね。

3.2 独立性

3.3 不偏推定量

そもそも、母集団の分散が未知であるため、不偏推定量を用いて検定を行います。この推定値の不確実性が、検定結果に影響を及ぼす可能性があるため、データの信頼性やサンプルサイズの検討が大事です。

サンプルサイズ設計ツールはこちら。

これらの前提条件が成立していることを確認することが、正確なF検定の実施には不可欠です。

4. F検定の実施手順

実際にF検定を行うための基本的な手順は以下の通りです。

4.1 不偏分散の計算

まず、各標本から不偏分散 ${S_1^2}$と ${S_2^2}$を計算します。実務では、分母に自由度（サンプルサイズ – 1）を用いて求めることが一般的です。

4.2 F統計量の算出

算出された不偏分散を用いて、F統計量を以下のように計算します。

$${F = \frac{S_1^2}{S_2^2}}$$

※ 通常、常に ${F \geq 1}$となるよう、大きい分散を分子に設定します。

4.3 臨界値の設定と検定

有意水準 ${\alpha}$ に対して、F分布の累積分布関数を用いて臨界値 ${F_\alpha}$を求めます。

つまり、次の条件を満たす ${F_\alpha}$​ を決定します。

$${\int_{F_\alpha}^\infty f(x; n_1 – 1, n_2 – 1) \,dx = \alpha}$$

計算したF統計量がこの臨界値 ${F_\alpha}$ より大きければ、帰無仮説「${\sigma_1^2 = \sigma_2^2}$​」を棄却し、2群間に有意な分散の差があると判断します。

5. 分散分析（ANOVA）におけるF検定の応用

F検定は、2群の分散比較だけでなく、多群間の平均の差の検定（分散分析：ANOVA）にも広く応用されています。分散分析では、全体の変動を以下の2つに分解します。

5.1 群間変動と群内変動

• 群間平方和（SSB：Between Sum of Squares）
  • 各群の平均値が全体の平均値からどれだけ離れているかを示す指標です。各群の平均は正規分布に従うため、SSBはカイ二乗分布の性質を利用できます。
• 群内平方和（SSW：Within Sum of Squares）
  • 各データポイントがその群の平均からどれだけ離れているかを示します。各群内のばらつきの指標として用いられます。

5.2 F統計量による平均の検定

分散分析では、群間変動の平均平方（MSB）と群内変動の平均平方（MSW）の比をF統計量として計算します。

$${F = \frac{MSB}{MSW} = \frac{\frac{SSB}{df_{\text{between}}}}{\frac{SSW}{df_{\text{within}}}} \sim F(df_{\text{between}},\, df_{\text{within}})}$$

このF値により、各群の平均値に統計的な差があるかどうかを検定します。

繰り返しになりますが、群間平方和 (SSB) は、群の平均が全体の平均からどれだけ離れているかを示し、これがカイ二乗分布に従います。

これは、各群の平均もまた正規分布に従うためです。

同様にして、群内平方和 (SSW) は、各データポイントがその群の平均からどれだけ離れているかを示し、この分布もカイ二乗分布に従います。これは、データポイントが各群内で正規分布に従うという仮定によります。

→ANOVAの論理構造は、結局は元データの正規分布仮定に強く依存しています。（前述の通り）

分散分析については、統計検定2級の鬼門となっております。
詳しくは、こちらの記事をご覧ください。