03/16/2025 / 最終更新日時 : 03/16/2025 bluest Python

DBSCANとは？密度ベースのクラスタリングを解説

DBSCANとは？

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）は、密度ベースのクラスタリングアルゴリズムであり、データ点の密度に基づいてクラスタを形成します。従来の距離ベースのクラスタリング手法（k-means等）と異なり、DBSCANは任意の形状のクラスタを検出できる点が特徴です。

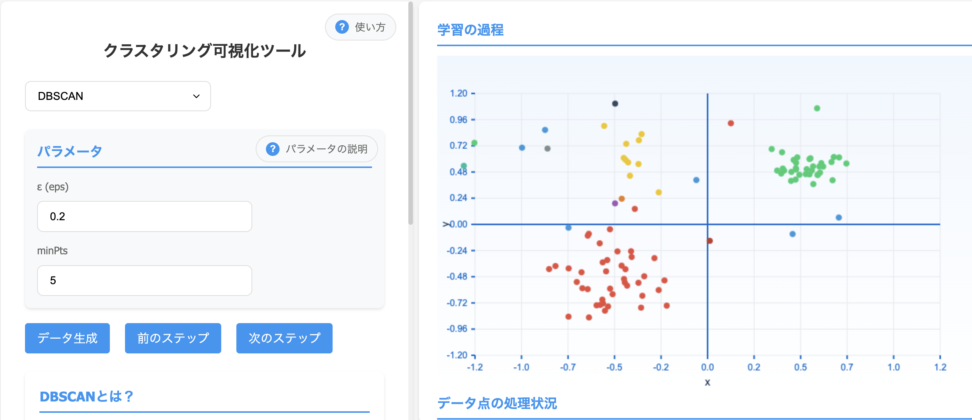
クラスタリング可視化ツールを使うと、クラスターが増えていく様子がわかると思います。

DBSCANの仕組み

DBSCANでは、データ空間内の各点を次の3つのカテゴリに分類します

  1. コアポイント：指定された半径（${ε}$）内に最小数（MinPts）以上のデータ点が存在する点
  2. ボーダーポイント：コアポイントではないが、コアポイントのε近傍内に存在する点
  3. ノイズポイント：コアポイントでもボーダーポイントでもない点

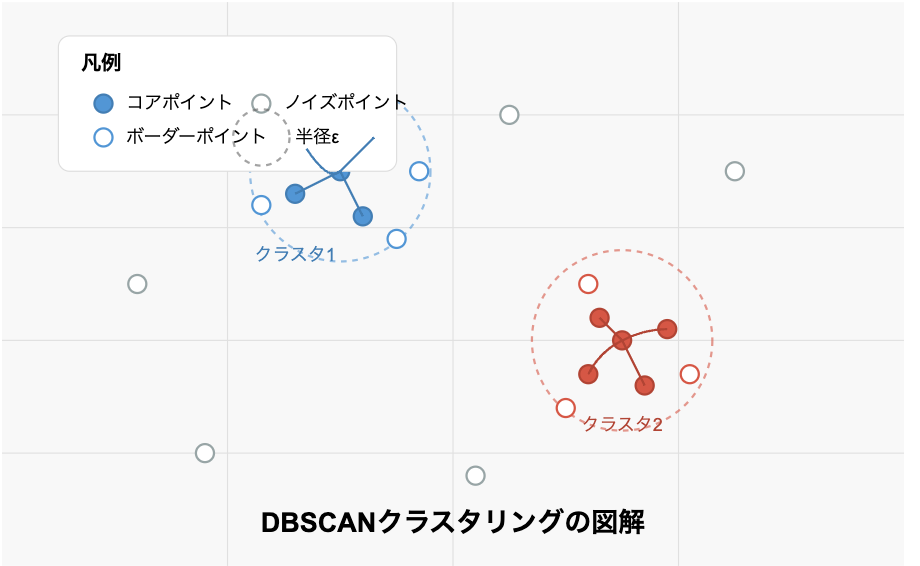
図で表すと、上のようになります。

各クラスタ内では密度連結によってコアポイントが結ばれています。また、クラスタの周辺にボーダーポイントが配置され、どのクラスタにも属さないノイズポイントがデータ空間内に散在しています。

DBSCANの主要な作業

  • コアポイントとその近傍のコアポイントを「密度連結」と見なし、同じクラスタに割り当てる
  • ボーダーポイントを最も近いクラスタに割り当てる
  • ノイズポイントをどのクラスタにも割り当てない（外れ値として識別）

DBSCANの数学的背景

DBSCANアルゴリズムの核心は「密度到達可能性（density-reachability）」と「密度連結（density-connectivity）」という概念にあります。

これらの概念を見ていきましょう。

密度到達可能性と密度連結

直接密度到達可能性

点${p}$から点${q}$が「直接密度到達可能」であるとは、以下の条件が成立することを意味します

  1. ${p}$がコアポイントである
  2. ${q}$が${p}$の${ε}$近傍内に存在する
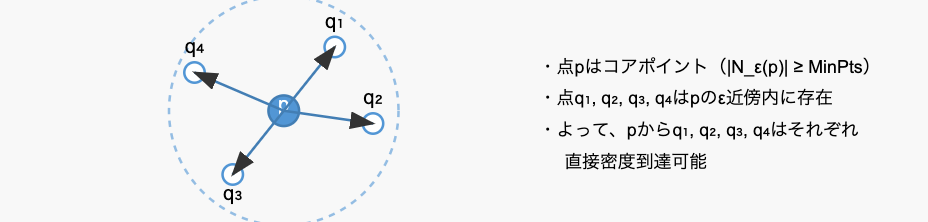
  • 青色で塗りつぶされた点${p}$はコアポイントです（MinPts以上の点がε半径内に存在）
  • 周囲の白抜きの点${q_1}$などは全て${p}$の${ε}$半径内に存在します
  • 矢印は${p}$から各点への「直接密度到達可能」な関係を示しています

数式で表すと

${p}$がコアポイント：${|N_{\varepsilon}(p)| \geq MinPts }$

qが${p}$の${ε}$近傍内：${q \in N_{\varepsilon}(p)}$

${N_{\varepsilon}(p)}$ は点${p}$の${ε}$近傍であり、${p}$からの距離が${ε}$以下の全ての点の集合です

$${N_{\varepsilon}(p) = \{q \in D | dist(p,q) \leq \varepsilon\} }$$

  • ${D}$はデータセット全体
  • ${dist}$は距離関数（通常はユークリッド距離）

密度到達可能性

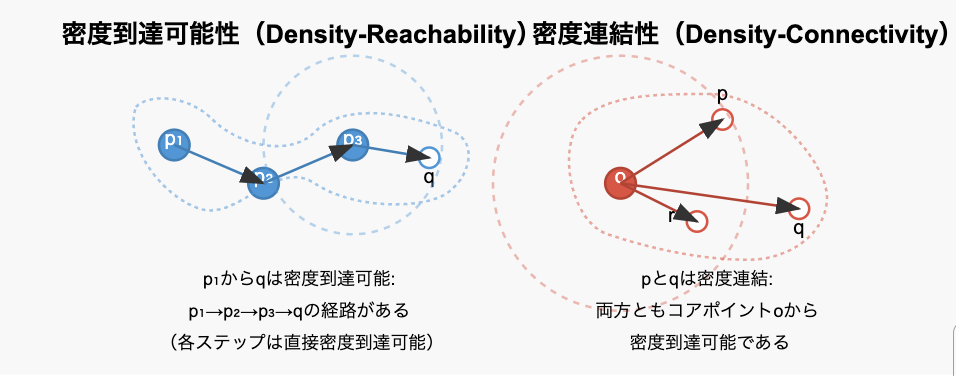
点${p}$から点${q}$が「密度到達可能」であるとは、点の列${p_1, p_2, …, p_n}$が存在し、${p_1 = p 、p_n = q}$であり、各${p_i}$​から${p_{i+1}}$が直接密度到達可能である場合を指します。

この関係は推移的ですが、対称的ではありません(図で言うと、qからp₁への逆方向の経路は存在しない可能性がある、ということ)

注意事項

${p}$から${q}$が密度到達可能であっても、${q}$から${p}$が密度到達可能であるとは限りません。

密度連結性

点${p}$と点${q}$が「密度連結」であるとは、点${o}$が存在し、${p}$と${q}$の両方が${o}$から密度到達可能である場合を指します。

数式で表すと

\exists o \in D : pと ${q}$ は ${o}$ から密度到達可能

密度連結性は対称的な関係です。

パラメータεとMinPtsの選択方法

DBSCANの性能は、εとMinPtsという2つのパラメータの選択に大きく依存します。これらのパラメータをどのように選べばよいのでしょうか？

MinPtsの選択

MinPtsの値は、データの次元数に基づいて選択することが一般的です。

経験則として

$${MinPts \geq D + 1 }$$

  • ${D}$はデータの次元数です。
管理人

低次元データでは4または5、高次元データではより大きな値（例：2倍の次元数）を選ぶことが推奨されています。

ノイズの多いデータセットでは、より大きなMinPts値を選択することで、より堅牢なクラスタリング結果が得られる傾向があります。

εの選択

${ε}$の値を選択するための一般的なアプローチは、k-距離グラフを使用する方法です

  1. 各点について、${k}$番目（${k = MinPts}$）に近い点までの距離を計算する
  2. これらの距離を昇順にソートしてプロットする
  3. グラフに屈曲点が現れる場合、それがεの適切な値の候補となる

数学的には、この屈曲点は以下の関数の二階微分が最大となる点として定義できます

$${f(x) = $ k-距離グラフにおける点 x$の値}$$

$${\varepsilon_{opt} = \arg\max_{x} |f”(x)|}$$

DBSCANの実装例

以下に、Pythonを使用したDBSCANの実装例を示します。scikit-learnライブラリを使用し、人工データセットに適用してみましょう。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons, make_blobs
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler

# データセットの生成
n_samples = 300
noisy_moons = make_moons(n_samples=n_samples, noise=0.05, random_state=42)
noisy_circles = make_blobs(n_samples=n_samples, centers=[[1, 1], [-1, -1], [1, -1], [-1, 1]], 
                           cluster_std=0.1, random_state=42)

# データセットの結合
X = np.vstack([noisy_moons[0], noisy_circles[0]])
X = StandardScaler().fit_transform(X)  # 標準化

# DBSCANの適用
db = DBSCAN(eps=0.3, min_samples=5)
labels = db.fit_predict(X)

# クラスタの数（ノイズを除く）
n_clusters = len(set(labels)) - (1 if -1 in labels else 0)
n_noise = list(labels).count(-1)

# 結果の可視化
plt.figure(figsize=(10, 7))
unique_labels = set(labels)
colors = plt.cm.Spectral(np.linspace(0, 1, len(unique_labels)))

for k, col in zip(unique_labels, colors):
    if k == -1:  # ノイズポイント
        col = 'k'  # 黒色
    
    class_member_mask = (labels == k)
    xy = X[class_member_mask]
    plt.scatter(xy[:, 0], xy[:, 1], s=50, c=[col], edgecolors='k', alpha=0.7)

plt.title(f'DBSCANによるクラスタリング結果: {n_clusters}クラスタ検出, {n_noise}ノイズポイント')
plt.xlabel('特徴量1')
plt.ylabel('特徴量2')
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()

この実装では、月形と円形のデータポイントを組み合わせた複雑な形状のクラスタを持つデータセットを生成し、DBSCANアルゴリズムを適用しています。

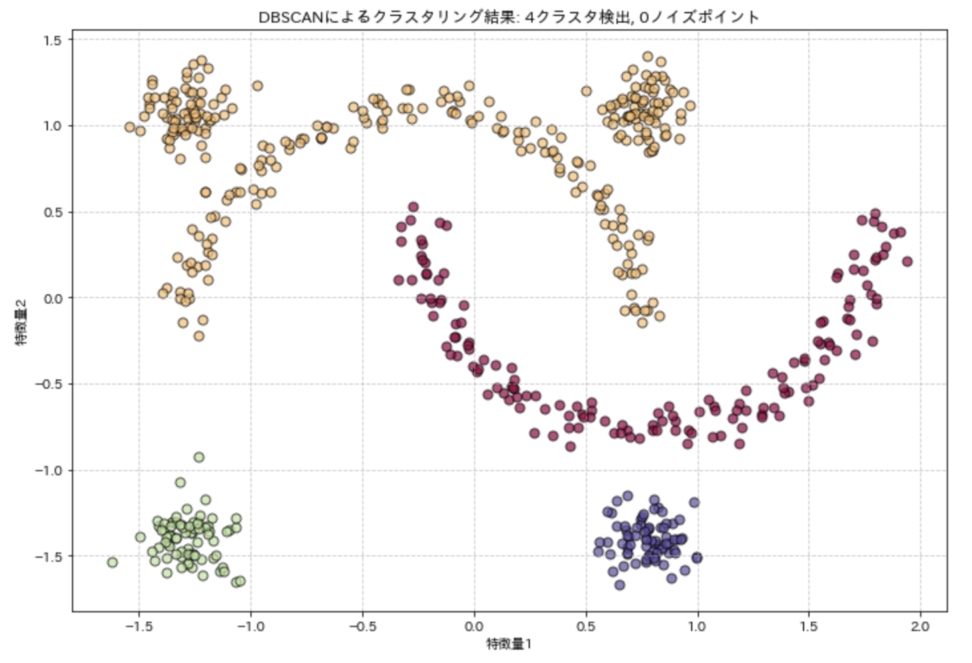
eps=0.3、min_samples=5というパラメータを使用しており、結果として複数のクラスタとノイズポイントが識別されます。

DBSCANのメリットデメリット整理

最後にメリットデメリットを整理してみます。

メリット

  1. 任意の形状のクラスタを検出可能
  2. クラスタ数の事前指定が不要
    • k-meansとは異なり、クラスタ数を事前に指定する必要がありません。
  3. ノイズの検出
    • アルゴリズムがノイズポイント（外れ値）を自動的に識別します。
  4. 異なる密度のクラスタの処理
    • 適切なパラメータ設定で、異なる密度を持つクラスタを検出できます（ただし、密度の差が極端に大きい場合は課題があります）。

デメリット

  1. パラメータ選択の難しさ
    • ${ε}$と${MinPts}$の適切な値を決定するのは、しばしば試行錯誤が必要です。
  2. 異なる密度のクラスタへの対応の限界
    • 1つのεとMinPts値だけでは、密度が大きく異なるクラスタを同時に適切に検出するのが難しい場合があります。
  3. 高次元データでの課題
    • 高次元空間では「次元の呪い」により、距離の概念が曖昧になり、アルゴリズムの性能が低下する可能性があります。
  4. メモリ要求が大きい
    • 大規模データセットでは、各点のε近傍を計算するためのメモリ要求が大きくなる場合があります。
  5. 計算複雑性
    • 最適化されていない実装では、計算時間が${O(n^2) }$となります。
管理人

このアルゴリズムの時間計算量は一般的に${O(n^2) }$ですが、空間インデックス（R木など）を使用することで${O(n \log n)}$に改善できる場合があります。

FOLLOW ME ！

カテゴリー
Python、マーケティング、大学数学
タグ
大学数学

前の記事

確率密度関数とは？確率質量関数との違いも解説
02/25/2025
Python

次の記事

スペクトラルクラスタリングとは？非線形データの分類
03/18/2025