【GLM】一般化線形モデルを解説|ポアソン回帰
今回はGLMと呼ばれる「一般化線形モデル(generalized liner model)」を解説します。
よく似た名前として、分散分析や共分散分析などの「一般線形モデル」が有りますが、一般線形モデルは正規線形モデルの一つでかなり違うのでご注意ください。
まずGLMで心得てほしいことは、「目的変数Yが正規分布に従わなくてもモデル化したい」ということです。
一般化線形モデル(generalized liner model)
「喫煙経験の有無と腎臓の直径は、調査開始時からの寿命と関係はあるのか」
今回は、以上のような架空の分析をしてみようと思います。
手順の説明をします。
1：喫煙経験有無が同数になるように、60歳前後の被験者を100人集める
2：腎臓の長さをレントゲンで測る
3：20年前後で被験者は全員亡くなった。
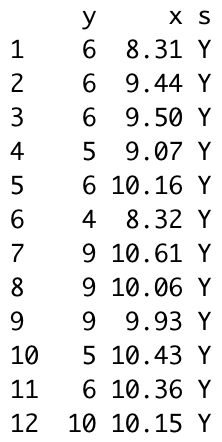
上の表は、観察データの抜粋です。
個体ごとに異なる説明変数(ここでは腎臓の直径)によって実験開始時からの平均寿命が変化する統計モデルです。
こうした統計モデルを観測データに当てはめ、予測を行うことをポアソン回帰と言います。予測は次回扱います。
人間の個体iの寿命は\(y\)年(観察開始から)であり、個体の属性である腎臓の直径\(x_i\)が観察されています。
また、喫煙経験がない50人は「コントロール群」といい、喫煙経験がどのように寿命に関わるのかを見る上で大切です。
CODE
data <- read.csv("smoking.csv")
data$x
data$y
data$s
#データの読み込みでは、xとyとs (喫煙有無)を分けてみましょう。
次に、それぞれのデータクラスを確認してみましょう。
class(data)
class(data$x)
class(data$y)
class(data$s)
→
[1] "data.frame"
[1] "numeric"
[1] "integer"
[1] "character"元データはdata.frameで、x(腎臓の直径)は実数型、y(実験開始からの寿命)は整数、s(喫煙有無)は文字として判定されました。
しかし、今回はsを因子(fantor)として扱いたいので、as.factor(data$s)を書きます。
as.factor(data$s)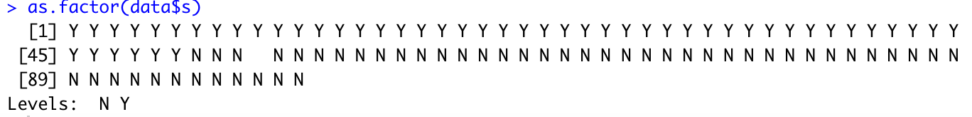
fantor型にうまく変換できました。Levelsが付与されました。
これはs列内での水準を示しています。
可視化
plot(data$x, data$y, pch = c(21,19)[as.factor(data$s)])
legend("topleft", legend = c("Y", "N"),pch = c(21,19))\(pch=(21,19)\)というのは、プロットの種類です。
今回は、白丸と黒丸です。
全部で25種類あります。
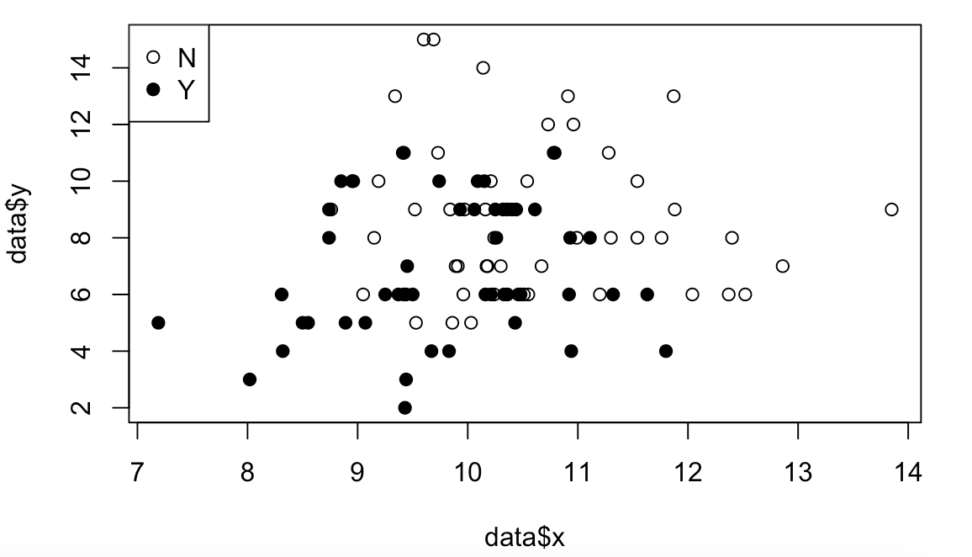
この表だけを見ると、
・喫煙経験がある人の方が、寿命が少なく、腎臓の直径もやや短め。
ということが大体わかるくらいです。
GLM(generalized liner model)とは
いよいよGLMを使ってみます。
前提として、「ある個体iにおいての寿命がyiである確率p(yi | λi)はポアソン分布に従う」と仮定します。
ポアソン分布について詳しく知りたい方は、【例題あり】ポアソン分布についてをご覧ください。
ここで、ある個体の平均寿命\(λ_i\)が以下のような式で表されるとします。
$$λ_{i}=exp(β_{1}+β_{2}x_{i})$$
わかりづらいので対数をとってみましょう。
$$logλ_{i}=β_{1}+β_{2}x_{i}$$
ここで、GLMの特徴を二つご紹介します。
１：線形予測子
線形予測子は、右辺のことです。切片の\(β1\)と、傾き\(β2\)と変数\(x_i\)(腎臓の直径)の積の和です。
入力されたxの数だけ、パラメータをかけたものです。
２：リンク関数
リンク関数は、左辺のことです。
３：確率分布
$$P(y_{n}|β)=Pois(y_{n}|λ_{n})$$
パラメーターβが得られた時の、\(y_i\)の分布のことです。
今回は「βが得られた時の寿命が\(y_i\)である確率」は、ポアソン分布に従うということになります。
一般線形モデルと一般化線形モデルの違い
パラメトリックな分析(母集団の分布を仮定する)をする場合の話です。
一般線形モデルは、データの分布が正規分布であることが仮定されています。
一方で、一般化線形モデルはデータが従う分布に対応する「リンク関数」を選択することで、より適した分析ができるというものです。
ある分布に従う確率変数Yがあるとして、その分布の平均をμとします。
μを変形した形\(f(μ)\)にすると、目的変数を線形で表すことができます。
これを一般化線形モデル(GLM)と呼びます。
今回は、目的変数がポアソン分布に従うとして、ポアソン分布の平均\(λ\)を、\(f(λ)\)として対数の形で表したものをリンク関数として表すことで、右辺を線形として扱える、というわけです。
推定値の求め方(estimate)
では、肝心の推定値の求め方についてです。
GLMは、作った統計モデルの対数尤度logLが最大になるパラメーターβの推定値を決定します。
対数尤度logLは以下のような式です。
$$logL(β_{1},β_{2})=\sum_{i=1}^{100}log\frac{λ_{i}^{y_{i}}exp(-λ_{i})}{y_{i}!}$$
iが1から100までの密度の積に対数をとっています。
対数をとると、積は和になるので計算が便利です。
左辺を最大にするβ1とβ2が求めたい最尤推定量になります。
βは\(logλ_i = β1 + β2X_i\)で隠れているだけです。
実際に推定量を求めてみましょう。
fitting <- glm(y ~ x, data = data, family = poisson(link = log))
fitting
数行のコードでGLMのポアソン回帰ができます。data=の右辺には、対象のデータフレームを入れます。family=poissonはバラつきの確率分布はポアソン分布ということです。
後々説明しますが、このfamilyというのは指数型分布族(exponential distribution family)から来ています。
GLMの目的変数yの確率分布は、指数型分布族というものしか適用できません。
link = log というのは、リンク関数は対数リンク関数であるという意味です。logλi のことです。
ポアソン分布でリンク関数を対数関数にしているので、ポアソン回帰モデル(対数線形モデル)と呼びます。
fittingを2行目で出力していますが、結果は以下のようになります。
1.63723と0.04957は、それぞれ切片β1とxiの係数β2の最尤推定量になります。
ポアソン回帰して作ったモデルが、データに対して最も当てはまりが良いパラメータAICも出てきました。
AICについてはこちらをご覧ください。
$$logλ_{i}=1.63723+0.04057x_{i}$$
こんな推定式が出来上がりました。xiは腎臓の直径で、λiは個体の寿命でした。
summary(fitting)summaryでもう少し詳細な内容も見てみましょう。
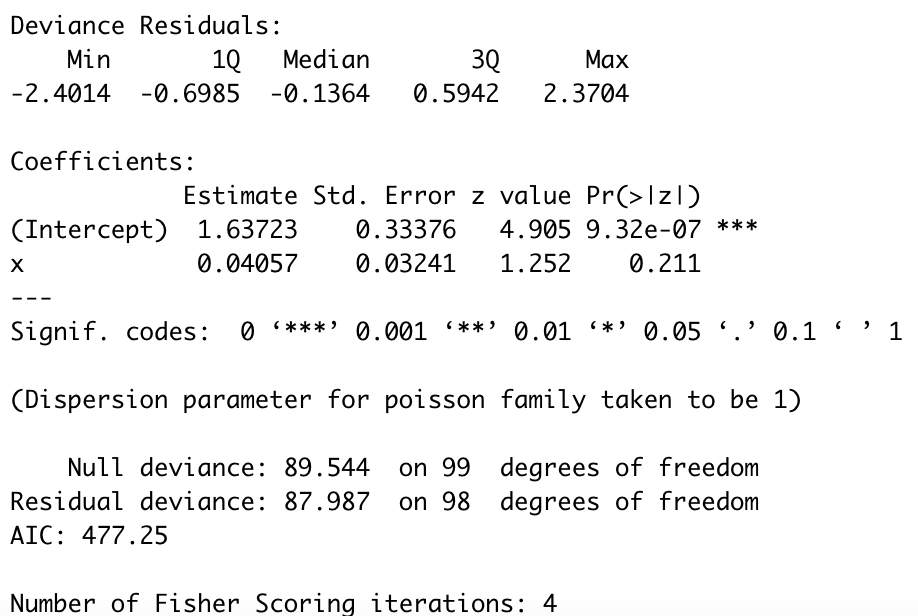
Std.Error：パラメータの標準誤差の推定値です。データセットを変えた時には、最尤推定量は一意に定まらないことを示唆しています。
詳しくは、【Standard Error】標準誤差を例題を通して解説。をご覧ください。
z value：最尤推定値をSEで割った統計量です。Wald統計量とも呼ばれています。
最尤推定については以下のコンテンツをご覧ください。
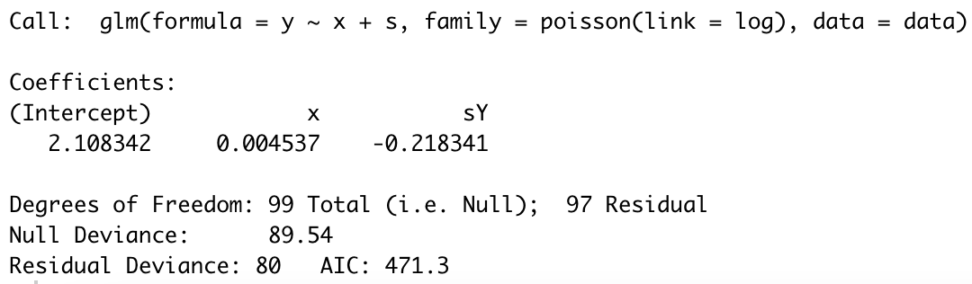
$$logλ_{i}=2.1083+0.0045x_{i}-0.2183s_{i}$$
喫煙経験があると、寿命にマイナスの影響があるという結果になりました。
では、最後にこのモデルでの最大対数尤度と、前のモデル(因子なし)の最大対数尤度を比較してみてみましょう。
> logLik(fitting)
#因子なし
'log Lik.' -236.6271 (df=2)
> logLik(fit.smoking)
#因子あり
'log Lik.' -232.634 (df=3)df=というのは、モデルの自由度のことです。
GLMでは、パラメーターの数がそのまま自由度になります。
因子があった方が若干最大対数尤度が大きいので、「当てはまりのよさ」でモデルを比較すると、因子(喫煙経験の有無)はあった方が良さそうです。
指数型分布族(exponential distribution family)
さて、ここからは補足です。
GLM(一般化線形モデル)の目的変数となる、確率変数Yの確率分布は指数型分布族と呼ばれます。
以下のようなeの指数関数の形で確率密度を表せるものは、すべて指数型分布族と呼びます。
例えば、正規分布やガンマ分布、ポアソン分布などの主要な確率分布は全て指数型分布族です。
$$f(x;θ)=ae^{θ^TS(x)-ψ(θ)}$$
例えば、\(N(μ,1)\)の正規分布を指数型分布族の形に直してみます。
$$f(x;μ)=\frac{1}{\sqrt{2π}}e^{-\frac{(x-μ)^2}{2}}=\frac{1}{\sqrt{2π}}e^{-\frac{x^2}{2}+μx-\frac{μ^2}{2}}$$
ここでいうθとは、期待値μのことなので、以下のようになります。
aはxの関数です。aとeの積では、指数同士を足し算しています。
$$a=\frac{1}{\sqrt{2π}}e^{-\frac{x^2}{2}},S(x)=x,ψ(θ)=\frac{θ^2}{2}$$
このような形だと何が嬉しいのかというと、ψ(θ)が狭義の凸関数になるということです。
つまり、この確率密度関数の対数尤度関数は凹関数(上に凸)になります。
よって尤度方程式の解は(存在するならば)一意的で，それが最尤推定量となる。
このように，指数型分布族 は比較的扱いやすい統計モデルです。(停留点を求めると、それが最尤推定量になるということ)
最尤推定量については、以下をご覧くださいませ。
