負の二項分布をわかりやすく解説
はじめに!
負の二項分布は、ポアソン分布や二項分布よりも過分散を扱いやすい柔軟なモデルとして知られています。
実験・観測データにしばしば見られる「期待値以上の分散」をうまく捉えることができ、免疫学や微生物学などの生物学的分野でも多用されています。
今回、免疫系の論文を読む機会があったのでまとめてみます。
まず負の二項分布の数学的定義や性質を解説し、次に論文をもとにT細胞クローン解析への応用例を詳述します。
2. 負の二項分布の基礎
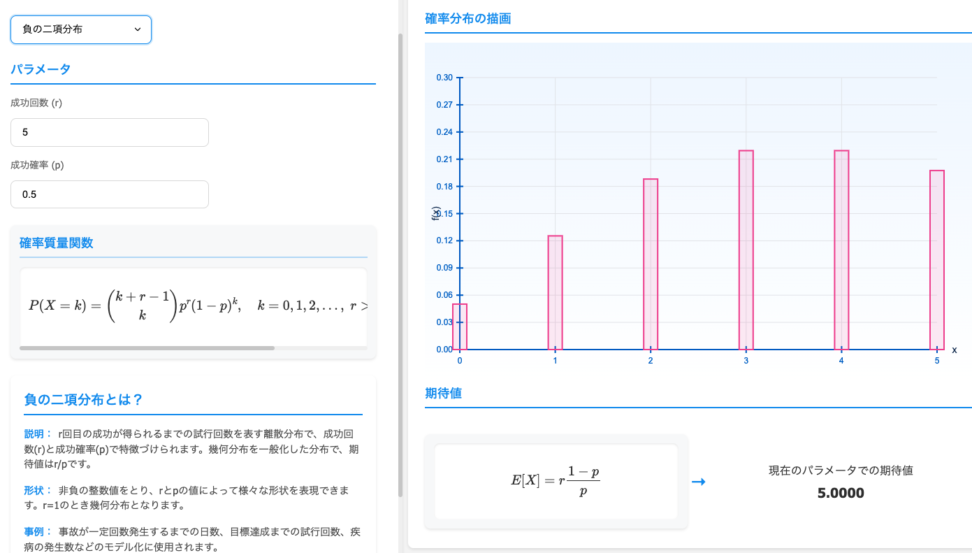
分布自体の可視化は、青の統計学-Ds Playground-の確率分布可視化ツールが便利です。
ぜひご覧ください。
2.1 定義と確率質量関数
負の二項分布は、
- 成功確率 ${p}$ のベルヌーイ試行を独立に繰り返したとき、
- ${r}$ 回目の成功を観測するまでに起こる失敗回数を表す確率分布です。
一般的な確率質量関数 (PMF) は次式で与えられます。
$${f(k;r,p)=\binom{k + n – 1}{n – 1}p^r(1-p)^k,(k=0,1,….)}$$
- ${r}$ : (整数)目標とする成功回数
- ${p}$ : 1回の試行における成功確率
- ${k}$ : 失敗回数(取り得る値は 0, 1, 2, …)
このとき、「${r}$回成功が得られるまでに${k}$回失敗する確率」を表していると解釈できます。
幾何分布との関係
負の二項分布において ${r=1}$ とすると、最初の1回成功が観測されるまでの失敗回数の分布、すなわち幾何分布に一致します。
2.2 期待値と分散
負の二項分布の期待値 ${E[X]}$と分散 ${\mathrm{Var}(X)}$ は以下の式で与えられます。
$${E[X] = \frac{r(1 – p)}{p}, \quad \mathrm{Var}(X) = \frac{r(1 – p)}{p^2}}$$
この分散は、ポアソン分布のように「期待値 = 分散」ではなく、
$${\mathrm{Var}(X) = E[X] \times \frac{1}{p}}$$
という形で、期待値よりもさらに大きくなる場合が許容されるため過分散を捉えやすいのが特徴です。
2.3 他の分布との比較
- 二項分布: 試行回数を固定し、その中での成功回数を数える → 負の二項分布は「成功回数を固定」し、そのために要する試行回数(あるいは失敗回数)をモデル化。
- ポアソン分布: レアな事象(低頻度)の回数をモデル化しやすいが、${\mathrm{Var} = E}$ という制約を持つ。これが破綻するような実験データ(いわゆる過分散)には不向き → 負の二項分布は柔軟。
- 幾何分布: 負の二項分布の特別な場合 (${r=1}$)。
2.4 負の二項分布の期待値とオッズ
先ほどの 負の二項分布 の期待値${E[X] = \frac{r(1-p)}{p}}$
を眺めると、${\frac{1-p}{p}}$が出てきます。
これはちょうど
$${\frac{1 – p}{p} = \frac{1}{\left(\frac{p}{1-p}\right)} = \frac{1}{\text{odds}}}$$
なので、
$${E[X] = r \times \frac{1-p}{p} = r \times \frac{1}{\text{odds}}}$$
すなわち、「期待される失敗回数 ${X}$」は「${r}$(成功回数)に対して、オッズの逆数を掛けたもの」になります。
逆に言えば、
$${E[X] \times \bigl(\text{odds}\bigr) = r}$$
- ここで ${X}$は確率変数ですが、${E[X]}$ はその平均値(期待値)。
- 期待値ベースで見れば「(失敗の期待値) × (成功のオッズ) = (目標成功回数)」という解釈ができる。
3. T細胞クローン頻度と負の二項分布
ここからは免疫学の分野において、どう負の二項分布が使われているのかを掘り下げていきます。
赤玉が入った袋〜とかサイコロとかの例よりも、実際に応用されている例を見た方が、
「なぜポアソン分布だとうまく事象をモデル化できなかったのか」とかの現場での実情が伺えて勉強になると思います。
3.1 背景:T細胞受容体(TCR)クローン解析の重要性
T細胞は、免疫応答の要となるリンパ球の一種であり、それぞれが特定の抗原を認識するためのT細胞受容体(TCR)を持ちます。
移植後(例:造血幹細胞移植後)には、特定のTCRクローンが急激に拡大し、拒絶反応や移植片対宿主病(GvHD, graft-versus-host disease) に影響を与えることが知られています。
TCRクローン頻度(あるいはリード数など)を観測した場合、その頻度データには以下の特徴があります。
- 非常に大きなばらつき(ごく一部のクローンが極端に拡大、他はほとんど増えない)。
- 観測データにはノイズ・サンプリング誤差がある。
- 期待値と分散の比が大きく、過分散の傾向がある。
このような状況で、ポアソン分布や単純な二項分布ではモデル化が難しく、負の二項分布が適しているケースが多いわけです。
3.2 論文「Microbiota dictate T cell clonal selection …」でのモデル
論文
Microbiota dictate T cell clonal selection to augment graft-versus-host disease after stem cell transplantation
では、移植後における微生物叢の状態がT細胞クローンの選択や拡大に影響を与え、結果的にGvHDを増幅するプロセスをモデル化しています。
そこでは、
- T細胞クローンの“平均的な観測頻度スケール”を ${n}$ とし、実際に観測される試行で成功(=検出)する確率を ${p}$ とみなす
- あるクローンが ${k}$ 回観測される(= リード数 ${k}$ が得られる)確率
として、負の二項分布を用いています。
論文中の解説(補足情報など)で見られるように、
$${P(C_1 = k) = \binom{k + n – 1}{n – 1} (1 – p)^k \, p^n \quad (k = 0, 1, 2, \dots) }$$
と表現することがあります(パラメータの表記ゆれは論文や資料によって異なりますが、上式は「${n}$回観測成功するまでに${k}$回失敗」という標準的な形になっています)。
ここで、
- ${n}$ : 「平均的な観測頻度」を表すパラメータ(例:理想的には10回観測できるはず)
- ${p}$ : 1回の観測試行で成功(クローンがリード数としてカウントされる)する確率
- ${(1−p)}$ : 観測に失敗する確率
というモデル解釈が可能です。
論文の文脈では、クローンの初期サイズのばらつきやサンプリングの偏り, 実際のシーケンスでのランダム性など、多くの要因を含めて「観測成功確率(${p}$)」と「理想的な繰り返し回数(${n}$)」に集約し、過分散を許容する形でリード数の分布を推定していると言えます。
3.3 なぜポアソン分布ではなく負の二項分布か?
T細胞クローンの分布をポアソン分布でモデル化すると、
- ${\mathrm{Var} = E}$の制限があり、「一部のクローンが極端に多く検出される」ような現象を十分に表現できません。
- 分散も期待値も強度${\lambda}$になります
- 実際は「数十~数百回検出されるクローン」と「1回も検出されないクローン」が混在し、その分散が期待値以上に肥大化しがち。
一方で負の二項分布は、${\mathrm{Var}(X) = E[X] \cdot \left( 1 + \frac{E[X]}{r} \right)}$
といった形でより大きな分散を許容でき、多くのクローンは検出されないが、一部が高頻度で検出されるといった非対称な分布を適切に表現できます。
4. 数式面でもう少し踏み込んでみる
4.1 モーメント母関数と特性関数
負の二項分布を確率変数 ${X}$ として、
- モーメント母関数 ${M_X(t)}$
$${M_X(t) = E[e^{tX}] = \left(\frac{p}{1 – (1-p)\,e^t}\right)^r}$$
- 特性関数 ${\phi_X(t)}$
$${\phi_X(t) = E[e^{i t X}] = \left(\frac{p}{1 – (1-p)\,e^{i t}}\right)^r}$$
が導かれます。
ここで、${(1-p)\,e^t}$や${(1-p)\,e^{i t}}$ の絶対値が1より小さい範囲で収束します。
特性関数やモーメント母関数を用いると、高次モーメントやキュムラントを体系的に計算でき、T細胞クローン頻度の高次のばらつき(尖度や歪度)まで分析可能です。
4.2 一般化負の二項分布(パラメータ${r}$の連続化)
生物学や医学の研究では、成功回数 ${r}$ が整数とは限らない状況(例えば「クローン数が実数パラメータとして扱われる」など)もあります。
そこで、${\Gamma}$関数を用いてパラメータ ${r}$ を実数(0より大きい)として扱う一般化負の二項分布が利用されることがあります。
これは解析手法の柔軟性を高める利点があります。
5. 実データ解析の流れ:パラメータ推定とモデル適合
TCRクローン頻度などのカウントデータに負の二項分布を当てはめる際は、以下のステップで進むことが多いです。
- 観測データ(各クローンのリード数 ${k_i}$)を取得。
- 最尤推定 (MLE) またはモーメント法 などで、${(r, p)}$や${(n,p)}$を推定する。
- 適合度検定(例えばカイ二乗検定、対数尤度比検定、情報量規準(AIC, BIC)など)で「負の二項分布が十分データを説明しているか」をチェック。
- 解析結果をもとに、クローンの増殖や分布の傾向を解釈する
- (例:高頻度クローンがどれくらいの割合で出現するか、など)。
5.1 Pythonでの例: 負の二項分布のパラメータ推定
実際にPythonで、観測データ counts (例えば各クローンのリード数) が与えられたときの最尤推定例を示します。
下記コードでは scipy 等を用いて、対数尤度を最大化する形でパラメータを推定します。
import numpy as np
import pandas as pd
from scipy.optimize import minimize
from math import comb, log
# サンプル:観測データ (カウント) とする
counts = np.array([0, 0, 1, 5, 10, 10, 10, 12, 15, 20, 30, 30, 31, 50])
def negbin_logpmf(k, r, p):
# k: 観測された失敗回数
# r: 成功回数(もしくは論文によっては観測したい回数)
# p: 成功確率
# PMF: (r + k - 1)C(k) * p^r * (1 - p)^k
# 対数を返す
return (log(comb(k + r - 1, k))
+ r * log(p)
+ k * log(1 - p))
def neg_log_likelihood(params, data):
# params: (r, p)
r, p = params
if r <= 0 or p <= 0 or p >= 1:
return np.inf
ll = 0.0
for k in data:
# k が 0, 1, 2, ... のカウント
ll += negbin_logpmf(k, r, p)
return -ll # 負の対数尤度
# 初期値を適当に設定
initial_params = np.array([5.0, 0.5])
# 最適化 (最尤推定)
res = minimize(
neg_log_likelihood,
initial_params,
args=(counts,),
method="Nelder-Mead"
)
if res.success:
r_mle, p_mle = res.x
print(f"推定されたパラメータ: r={r_mle:.3f}, p={p_mle:.3f}")
# 期待値や分散を計算
E = r_mle * (1 - p_mle) / p_mle
Var = r_mle * (1 - p_mle) / (p_mle**2)
print(f"期待値={E:.3f}, 分散={Var:.3f}")
else:
print("最適化に失敗しました")
このようにして推定された ${(r,p)}$ を用いて、T細胞クローン分布がどの程度過分散か、また観測されたリード数のばらつきがどのように説明できるかを検討します。
まとめ!
本記事では、負の二項分布の数理的な定義・性質・他の分布との関係を概観した上で、特にT細胞クローン解析における具体的な活用例を示しました。
生体内のクローン拡大は一部のクローンが極端に高頻度化する非対称性を伴うことが多いため、過分散を許容できる負の二項分布モデルが適切と考えられます。
実際、論文
Microbiota dictate T cell clonal selection to augment graft-versus-host disease after stem cell transplantation
の事例でも、観測データのノイズやリードカウントの偏りを考慮しながら、T細胞クローンの「検出される回数(リード数)」をモデル化するために負の二項分布が利用されていました。

分散と期待値が一致するポアソン分布だと、「流石にもうちょい分散が大きいよね?」となり、今回の分布選択に至ったようです。
実際の研究デザインで「ポアソン分布では捉えきれない過分散をどう扱うか?」という場面において、ぜひこの分布を思い出していただければ幸いです。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!




