内生性と外生性の概念と操作変数法による内生性の問題の解決方法をわかりやすく。
内生性・外生性の違いと操作変数法について
はじめに
こんにちは、青の統計学です!
今回は、経済学の授業などでよく出るワード「内生性と外生性」 について解説します。
さて、「相関は因果を意味しない」という言葉を耳にしたことがあるでしょう。
ビジネスでもアカデミアでも、我々はある変数 $X$ が別の変数 $Y$ にどれだけ影響を与えているか、その「真の効果」を知りたいと考えます。例えば、「教育年数が増えると賃金はどれだけ上がるのか」といった問いです。しかし、単純な回帰分析(最小二乗法、OLS)を適用しただけでは、多くの場合、この真の効果を正確に捉えられたとは言い難いです。
というのも、観測できるデータには、常に「内生性(Endogeneityと言います)」というバイアスが潜んでいる可能性があるからです。
本記事では、この内生性と対をなす外生性の概念を数学的背景から掘り下げ、そして、この問題を解決するための操作変数法の論理と仕組みを解説します。
外生性の本質とは?
私たちが頻繁に利用する線形回帰モデルは、次のように表されます。
$${y_i = \beta_0 + \beta_1 x_i + \epsilon_i}$$
- $y_i$ は被説明変数(結果)
- $x_i$ は説明変数(原因)
- $\epsilon_i$ は誤差項(モデルで説明できない残りの部分)
ですね。
そして $\beta_1$ が私たちが推定したい $x$ の $y$ に対する効果(係数)です。
最小二乗法(OLS)が、この $\beta_1$ を一致性(標本サイズが大きくなるにつれて真の値に収束する性質)を持って推定できるためには、前提条件が必要です。それが「外生性(Exogeneityと言います)」の仮定です。
回帰分析の基本的な理解をしたい方はこちらの記事をご覧ください。
外生性の数学的定義
さて、外生性とは、説明変数 $x$ と誤差項 $\epsilon$ の間に相関がないという仮定です。
数学的には、次のように表現されます。
$${E[\epsilon_i | x_i] = 0}$$

つまり、「$x$ の値が何であっても、誤差項 $\epsilon$ の平均はゼロである」ということです。
これは、説明変数 $x$ が誤差項 $\epsilon$ に含まれる観測されない要因と一切関係がないことを意味します。
この外生性の仮定が満たされていれば、OLS推定量 $\hat{\beta}_{OLS}$ は一致性を持ち、真の因果効果 $\beta_1$ に近づくことが保証されます。
内生性:仮定が崩れたときに生じる悲劇
しかし、もしこの外生性の仮定が崩れ、説明変数 $x$ と誤差項 $\epsilon$ の間に相関が生じてしまったらどうなるでしょうか。この状態こそが内生性がある、という状態です。
$${E[\epsilon_i | x_i] \neq 0 \quad \text{または} \quad Cov(x_i, \epsilon_i) \neq 0}$$
内生性が存在すると、OLS推定量 $\hat{\beta}_{OLS}$ は真の値 $\beta_1$ からどれだけズレるか(バイアス)が、以下の式で示されます。
$${\operatorname{plim} \hat{\beta}_{OLS} = \beta_1 + \frac{Cov(x, \epsilon)}{Var(x)}}$$

ここで $\operatorname{plim}$ は確率収束を意味します。分布収束とは異なるのでご注意ください。
つまり、内生性がある場合($Cov(x, \epsilon) \neq 0$)、標本サイズをいくら大きくしても、OLS推定量は真の値 $\beta_1$ に収束せず、バイアス項 $\frac{Cov(x, \epsilon)}{Var(x)}$ の分だけズレた値を推定してしまうのです。
なぜ誤差項と相関するのか
内生性が生じる主な原因は、大きく分けて三つあります。これらはすべて、モデルの「外部」ではなく「内部」で問題が発生しているという点で共通しています。
一つずつ見ていきましょう。
欠落変数バイアス
これが内生性の最もメジャーな要因です。
先ほどの「教育年数と賃金」の例で考えてみましょう。賃金 ($Y$) は教育年数 ($X$) だけでなく、個人の能力や努力といった観測できない要因にも影響されます。
もし、能力が高い人ほど教育年数も長い傾向にあるとすれば、能力は $X$(教育年数)と相関します。そして、能力はモデルに含まれていないため、誤差項 $\epsilon$ の一部となります。結果として、$X$ と $\epsilon$ が相関し、内生性が生じるといったプロセスです。
この場合、OLSは教育年数の効果を過大評価してしまいます。なぜなら、OLSが推定した係数には、教育年数そのものの効果だけでなく、教育年数と相関する「能力」の効果までが上乗せされてしまうからです
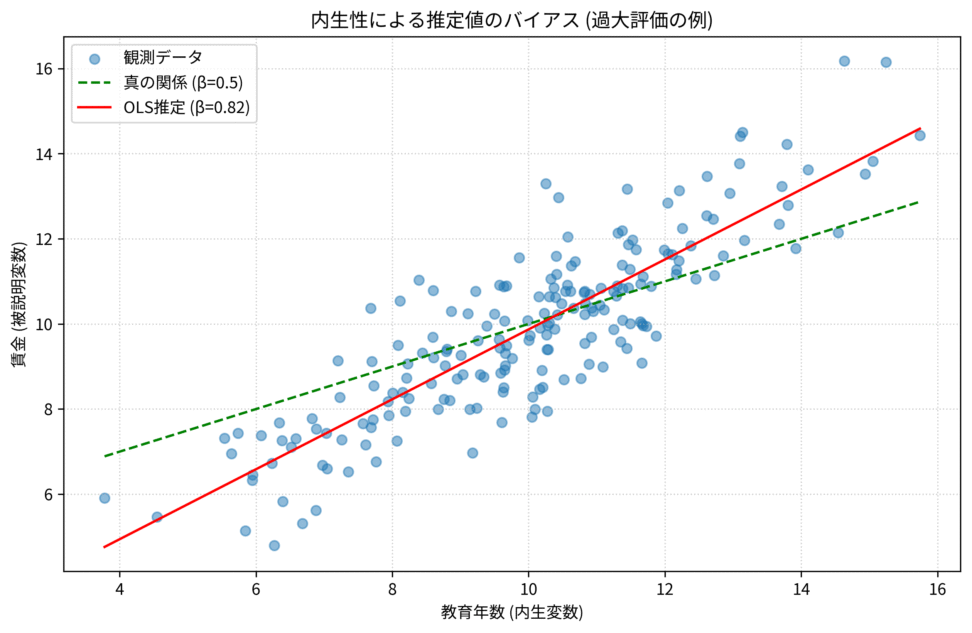
上の図は、真の係数 $\beta=0.5$ に対し、OLS推定値 $\hat{\beta}_{OLS} \approx 0.82$ と過大評価されている様子を示す散布図と回帰線です。
同時決定性
$X$ が $Y$ に影響を与え、$Y$ もまた $X$ に影響を与えるという、双方向の因果関係が存在する場合にも内生性が生じます。
例:供給と需要。
- 価格 ($X$) が需要量 ($Y$) に影響を与える(需要曲線)。
- 需要量 ($Y$) が価格 ($X$) に影響を与える(供給曲線)。
この場合、価格 $X$ は、需要曲線における誤差項(例えば、突発的なブーム)と相関してしまいます。なぜなら、ブームが起きれば需要量 $Y$ が増え、それに応じて価格 $X$ も変動するからです。
これは、デジタルマーケティングの領域でデータサイエンスに携わっている自分も頭をかかえたポイントです。例えば、コンバージョン(予約数とか)を上げるために、サイトのクチコミ総数を増やそうという試みの際に、自社サイト経由の予約が増えれば、構造的にはクチコミが増えるので、適切な因果関係と記述するのが難しいです。
測定誤差
ちょっと細かいですが、説明変数 $X$ が不正確に測定されている場合も、内生性の原因となります。真の値 $X^*$ と観測値 $X$ の間に誤差 $u$ があるとすると、$X = X^* + u$ です。
この測定誤差 $u$ が誤差項 $\epsilon$ に混入し、結果として $X$ と $\epsilon$ が相関してしまうのです。
操作変数法とは?

さて、内生性と外生性の話がわかったところで、操作変数法について学びましょう。
内生性の問題は、説明変数 $X$ に「真の効果」と「バイアスを生むノイズ」が混ざっているために起こります。操作変数法の目的は、この $X$ からノイズを取り除き、「真の効果」のみを抽出することです。
操作変数法では、操作変数 $Z$と呼ばれる第三の変数を利用します。この $Z$ は、内生変数 $X$ の変動のうち、誤差項 $\epsilon$ と無関係な部分だけを抽出するためのフィルター的な役割を果たします。
操作変数 $Z$ が満たすべき条件は、二つの条件に集約されます。
操作変数の二つの条件
操作変数 $Z$ は、以下の二つの条件を同時に満たさなければなりません。
関連性:内生変数 $X$ を動かす力があること
操作変数 $Z$ は、内生変数 $X$ と相関している必要があります。
$${Cov(Z, X) \neq 0}$$
もし $Z$ が $X$ と全く相関していなければ、 $Z$ は $X$ の変動を説明する情報を持たないため、フィルターとして機能しません。この条件が満たされない場合、詳しくは省略しますが、弱操作変数の問題が生じ、IV推定量は不安定になります。
除外制約:誤差項 $\epsilon$ と無関係であること
操作変数 $Z$ は、被説明変数 $Y$ に、内生変数 $X$ を通じてのみ影響を与え、誤差項 $\epsilon$ とは相関がない必要があります。
$${Cov(Z, \epsilon) = 0}$$
これは、 $Z$ が $Y$ に直接影響を与えたり、誤差項 $\epsilon$ に含まれる欠落変数(例:能力)と相関したりしてはいけない、という条件です。この条件が満たされて初めて、 $Z$ は $X$ の変動のうち「バイアスを含まないきれいな部分」だけを抽出できるのです。
ドメイン的に全然関係なさそうなものを選ぶ必要があるので、この除外制約が難しいですね。
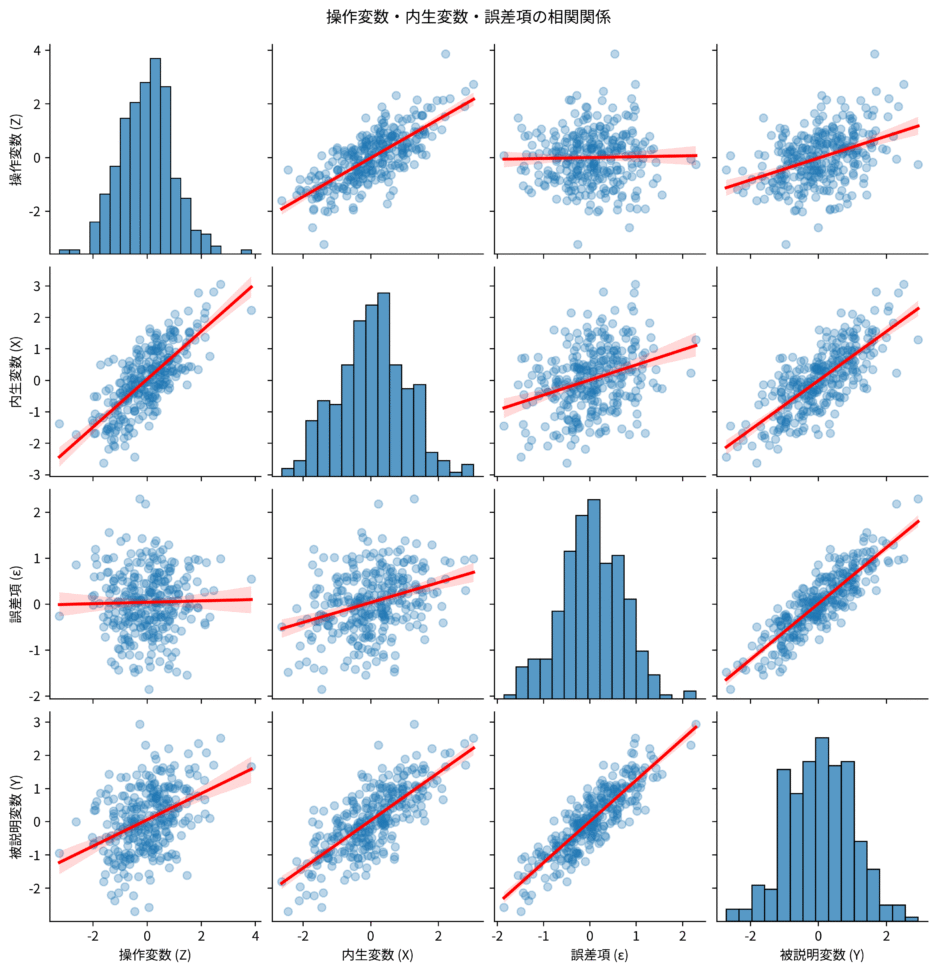
図:ZとXは相関があるが、Zと$\epsilon$は相関がない様子を示す散布図行列
備考:自然実験と操作変数法
操作変数は、自然実験から見出されます。自然実験とは、研究者が意図せずとも、自然発生的にRCTに近い状況が生まれる現象を指します。
例えば、「教育年数と賃金」の例で、親の教育年数や、居住地から大学までの距離といった変数が操作変数として使われることがあります。これらは、個人の能力($\epsilon$)とは直接相関しないが、教育年数($X$)には影響を与える、という論理に基づいています。
操作変数法は、この自然実験の「ランダムな割り当て」に相当する部分($Z$ が $X$ に与える影響)だけを抽出して利用する手法です。操作変数 $Z$ は、そうそう見つかるものではなく、ビジネスの現場ではあまり見られないです。
IV推定量の数学的表現
操作変数 $Z$ がこれらの条件を満たす場合、IV推定量 $\hat{\beta}_{IV}$ は、OLS推定量とは異なり、一致性を持ちます。
$${ \hat{\beta}_{IV} = \frac{Cov(Z, Y)}{Cov(Z, X)} }$$

$Z$ と $Y$ の共分散を $Z$ と $X$ の共分散で割ることで、 $Z$ を通じた $X$ の変動が $Y$ に与える影響を測っていることを示しています。
2段階最小二乗法(2SLS):IVを実践するプロセスについて
操作変数法を実際に適用する最も一般的な手法が、2段階最小二乗法です。名前の通りですが、OLSを2回に分けて実行することで、内生性の問題を解決します。
第1段階:内生変数 $X$ の「純粋な変動」を抽出する
まず、内生変数 $X$ を、操作変数 $Z$ と、モデルに含まれる他のすべての外生変数(もしあればですが)で回帰します。
$${X_i = \pi_0 + \pi_1 Z_i + v_i}$$
この回帰から得られる $X$ の予測値 $\hat{X}$は、操作変数 $Z$ の影響のみを受けた $X$ の変動部分を表します。
$${ \hat{X}_i = \hat{\pi}_0 + \hat{\pi}_1 Z_i }$$
操作変数 $Z$ は誤差項 $\epsilon$ と無相関であるため、この $\hat{X}$ もまた、誤差項 $\epsilon$ と無相関になります。つまり、$\hat{X}$ は $X$ のうち「バイアスを含まない純粋な部分」だけを抽出した変数、つまり外生変数として機能するのです。

2SLS 第1段階:操作変数 Z による X の予測
(ZとXの散布図と、Zによって予測された$\hat{X}$の回帰線)
第2段階:純粋な変動を用いて $Y$ を回帰する
次に、元のモデルの $X$ を、第1段階で得られた予測値 $\hat{X}$ に置き換えて回帰を行います。
$${Y_i = \beta_0 + \beta_1 \hat{X}_i + u_i}$$
この第2段階で推定される $\hat{\beta}_{2SLS}$ は、内生性の問題が解決された、一致性を持つ因果効果の推定量となります。
なぜなら、$\hat{X}$ は $X$ のうち $Z$ によって動かされた部分、すなわち $\epsilon$ と無相関な部分だけを使っているからです。これにより、欠落変数などのバイアス要因が $\hat{X}$ に混入することを防ぎ、真の因果効果 $\beta_1$ を正確に推定できるというわけです。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!






