ローレンツ曲線・ジニ係数・パレート分布をまとめて理解｜不平等を数学で捉える
こんにちは、青の統計学です。
今回は、ローレンツ曲線とジニ係数について学んでいきます。
高校の政治経済とかでも出ますね。
ローレンツ曲線は不平等の視覚的表現を可能にし、ジニ係数はその不平等度を数値で表現する、というのはだいたいわかりますが、導出やその仕組みはあまり深く理解できていない方も多いと思います。
24年の統計検定1級の「社会科学の問題では、「ローレンツ曲線を書いてください」という問題が出ましたね！
今回の記事では、不平等現象の背後にある確率的メカニズムを説明する理論的基盤となっているパレート分布についても言及しようと思います。
ローレンツ曲線の数学的基盤
累積分布を起点に
ローレンツ曲線を理解するためには、まず累積分布の概念から始めるのが自然ですね。
例えば、ある国の100人の国民の所得データがあるとしましょう。この100人を所得の低い順に並べて、「下位何％の人々が、全体の所得の何％を占めているか」を調べたくなるのは自然な発想です。
この発想を数学的に一般化したものがローレンツ曲線です。集団全体を確率変数Xで表現し、その期待値をμとします。ローレンツ曲線L(F)は、下位集団の割合Fを変数として、次のように定義されます
$${L(F) = \frac{1}{\mu} \int_0^F x(F’) dF’}$$
x(F)は累積分布関数F(x)の逆関数ですね。
つまり、${F(x(F)) = F}$という関係が成り立ちます。
この定義は一見複雑に見えますが、実は非常に直感的な意味を持っています。
定義の直感的理解
上の積分${\int_0^F x(F’) dF’}$は、下位F割の集団が持つ確率変数の値の合計を表しています。
これを全体の期待値μで割ることで、「下位F割の集団が全体の何割を占めているか」という比率が得られます。
つまり、ローレンツ曲線L(F)は、累積人口比率Fに対する累積所得比率を表現しているのです。
確率密度関数f(x)を用いると、ローレンツ曲線は以下のようにも表現できます
$${L(F) = \frac{1}{\mu} \int_{-\infty}^{x(F)} x f(x) dx}$$
この表現により、ローレンツ曲線が確率分布の性質と密接に関連していることがわかります。
完全平等線との関係
ローレンツ曲線を理解する上で重要なのが、完全平等線との比較です。
完全平等線は、y = xという45度の直線で表されます。
これは、「下位F割の人々が、全体のF割を占める」という完全に平等な状態を表しています。
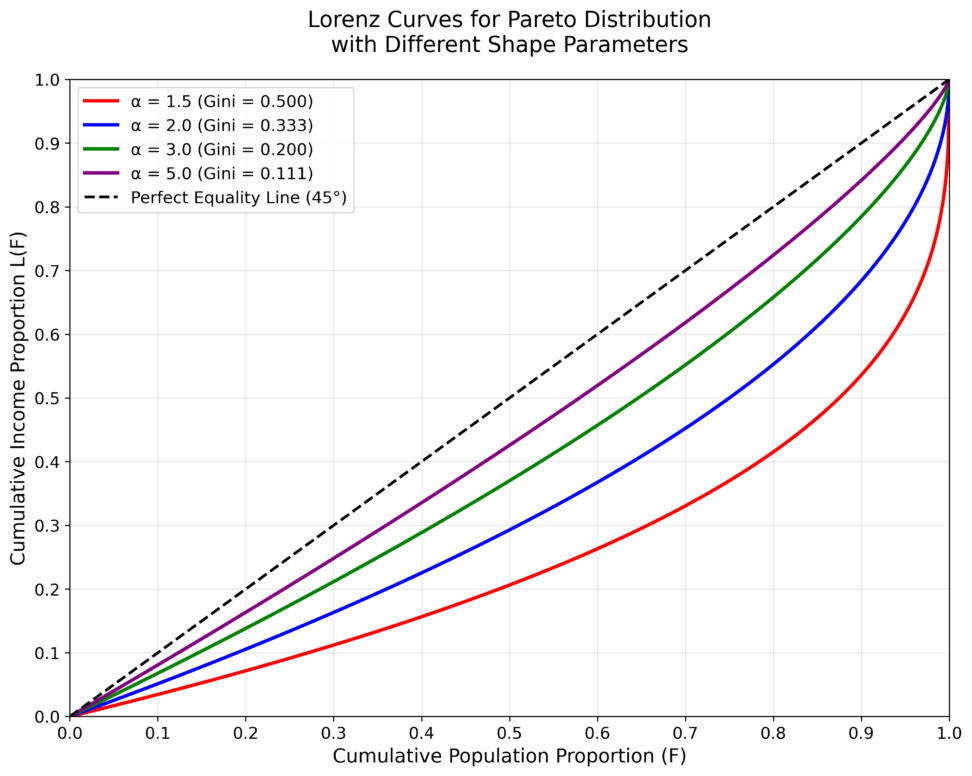
現実のローレンツ曲線は、数学的性質により必ずこの完全平等線の下側（または上側）に位置します。
これは、ローレンツ曲線の凹性（concavity）という性質から導かれます（性質は後述します。）
具体的には、L”(F) ≥ 0が成り立ち、曲線は下に凸の形状を持ちます。
ローレンツ曲線の数学的性質
1. 境界条件: L(0) = 0, L(1) = 1
2. 単調性: L'(F) ≥ 0（非減少関数）
3. 凹性: L”(F) ≥ 0（下に凸）
4. 正規化: 期待値μが有限かつ非零である場合にのみ定義される
これらの性質は、ローレンツ曲線が不平等度を測定する上で適切な指標であることを数学的に保証しています。特に凹性は、「富の集中度が高いほど曲線が完全平等線から離れる」という直感的な理解と一致しています。
ローレンツ曲線の傾きL'(F)は、累積分布の逆関数x(F)を全体の期待値μで割ったものに等しくなります
$${L'(F) = \frac{x(F)}{\mu}}$$
この関係式は、ローレンツ曲線の各点での傾きが、その点での所得水準と全体平均の比率を表していることを示しています。
つまり、曲線の傾きの変化を観察することで、所得分布の特徴を読み取ることができるのです。
ジニ係数：不平等の定量化
続いては、ジニ係数についてです。
ローレンツ曲線から自然に導かれる指標
さて、ローレンツ曲線は不平等の視覚的表現として優れていますが、異なる分布を定量的に比較するためには、単一の数値指標が必要ですね。
この要求に応えるのがジニ係数（Gini coefficient）というやつです。
ジニ係数は、ローレンツ曲線と完全平等線の間の面積に基づいて定義されます。
幾何学的解釈：面積比としての定義
ジニ係数の幾何学的定義を数式で表現すると
$${G = \frac{\text{完全平等線とローレンツ曲線で囲まれた面積}}{\text{完全平等線より下の三角形の面積}}}$$
図で見るのが一番早いと思います。
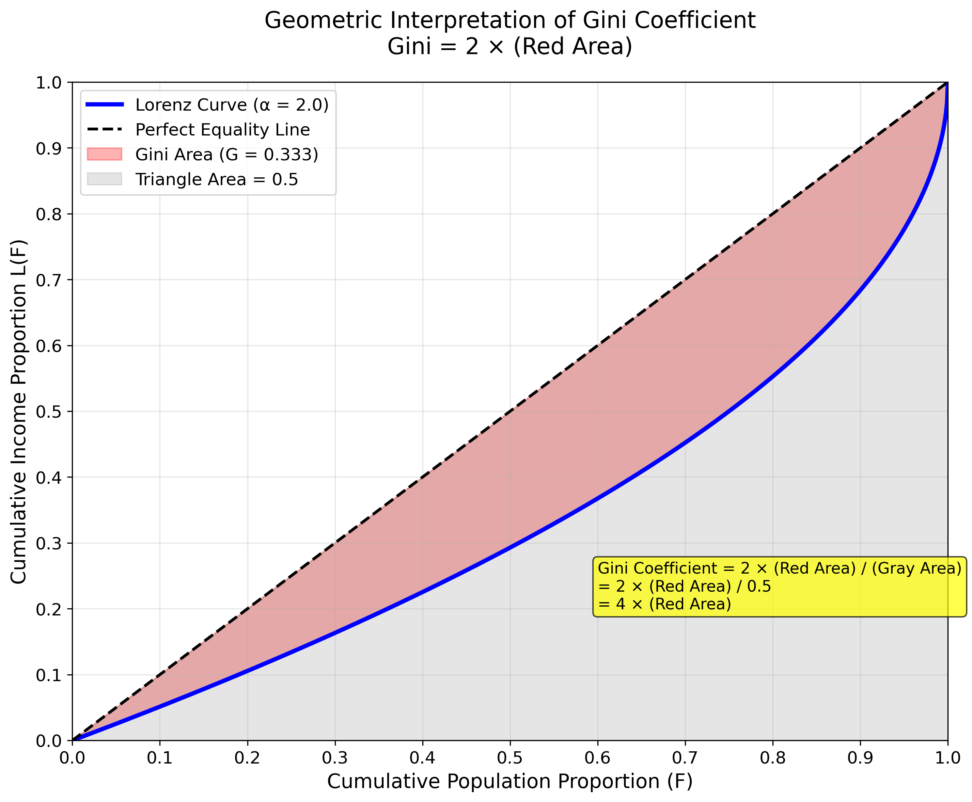
完全平等線より下の三角形の面積は1/2なので、ジニ係数は以下のように表現できます
$${G = 2 \times \text{（完全平等線とローレンツ曲線で囲まれた面積）}}$$
これを積分で表現すると
$${G = 1 – 2\int_0^1 L(F) dF}$$
この式は、ジニ係数がローレンツ曲線の下側の面積と直接的な関係にあることを示しています。ローレンツ曲線が完全平等線に近いほど積分値は大きくなり、ジニ係数は小さくなります。逆に、ローレンツ曲線が完全平等線から離れるほど、ジニ係数は大きくなります。
0から1の範囲での解釈
– G = 0: 完全平等（全員が同じ所得を持つ状態）
– G = 1: 完全不平等（一人がすべてを独占する状態）
ジニ係数は常に0から1の間の値を取ります
どこから高くてどこから低いかなどの基準は、当然ですが文脈や分析対象によって異なります。
さて、数学的な性質を見てみましょう。
ジニ係数の数学的性質
1. 正規化: 0 ≤ G ≤ 1
2. 匿名性: 個人の順序を入れ替えても値は変わらない
3. 人口独立性: 同じ分布を持つ集団を結合しても値は変わらない
4. 相対性: すべての値を定数倍しても値は変わらない
特に嬉しいのは、相対性の性質です。インフレーションや通貨の違いに影響されずに不平等度を比較できることを意味しています。
パレート分布
さて、ここからは少し理論的背景に入っていきます。
聞き慣れないかもしれませんが、確率分布「パレート分布」というものをご紹介します。
確率密度関数の数学的構造
パレート分布の確率密度関数は、以下のように定義されます
$${f(x) = \frac{\alpha x_m^\alpha}{x^{\alpha+1}}, \quad x \geq x_m}$$
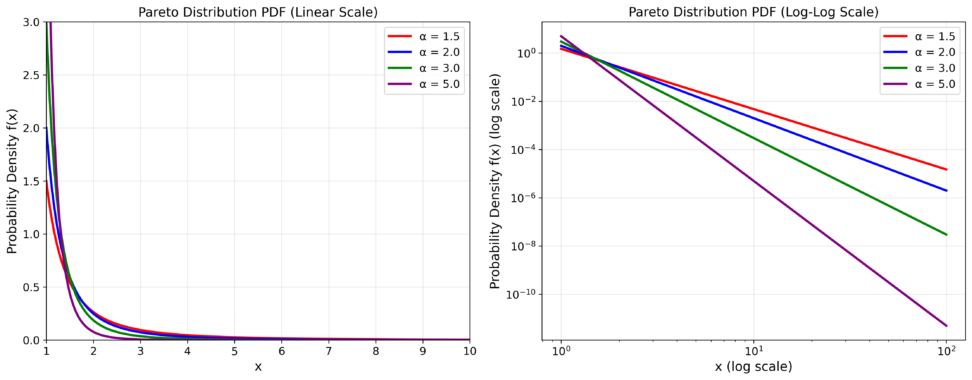
- αは形状パラメータ：分布の「重さ」を制御するパラメータです
- αが小さい（例：α = 1.5）：非常に重い裾を持ち、極端な値が出現しやすい
- – αが大きい（例：α = 5）：比較的軽い裾を持ち、極端な値は稀
- xₘは最小値パラメータ
この関数の特徴的な形は、xₘから始まって急激に減少し、右側に長い裾を引く分布を作り出します。
実際にパラメータを動かして、確率分布を動かしてみたい方は、「青の統計学のDsPlayground」の確率分布可視化ツールをご覧ください。
確率密度関数から復習したい方はこちらがおすすめです。
累積分布関数の導出
確率密度関数から累積分布関数を導出してみましょう
$${F(x) = \int_{x_m}^x \frac{\alpha x_m^\alpha}{t^{\alpha+1}} dt}$$
この積分を計算すると
$${F(x) = 1 – \left(\frac{x_m}{x}\right)^\alpha}$$
この累積分布関数は、パレート分布の重要な性質を明確に示しています。
特に、P(X > x) = (xₘ/x)^αという形で表される生存関数は、べき乗則（power law）の典型的な形です。
期待値と分散の計算
ここからは、やや込み入った話です。
期待値と分散を見ていきましょう。
パレート分布の期待値は、α > 1のときのみ有限値を持ちます。
$${E[X] = \frac{\alpha x_m}{\alpha – 1}, \quad \alpha > 1}$$
分散は、α > 2のときのみ有限値を持ちます
$${Var[X] = \frac{\alpha x_m^2}{(\alpha – 1)^2(\alpha – 2)}, \quad \alpha > 2}$$
αが小さい場合、期待値や分散が発散してしまうのです。これは、極端に大きな値が出現する確率が高すぎるためで、現実世界の多くの現象でαが1より大きな値を取る理由でもあります。
小ネタ｜べき乗則との関係
パレート分布の特徴は、べき乗則に従うことです。
生存関数P(X > x) = (xₘ/x)^αを対数スケールで表示すると
$${log P(X > x) = \alpha log x_m – \alpha log x}$$
これは傾き-αの直線になります。この性質により、パレート分布は「スケール不変性」を持ちます。つまり、どの範囲を見ても同じような比率で分布が続いています。
3つの概念の深い関連性
最後に、３つの概念がどう繋がるかを考えてみます。
特に、パレート分布に従うデータのローレンツ曲線とジニ係数は、解析解を持つことが知られています。
パレート分布のローレンツ曲線：解析的導出
パレート分布の累積分布関数${F(x) = 1 – (xₘ/x)^α}$から、ローレンツ曲線を導出してみましょう。
まず、累積分布関数の逆関数を求めます
$${x(F) = x_m (1-F)^{-1/\alpha}}$$
次に、ローレンツ曲線の定義に従って積分を計算します
$${L(F) = \frac{1}{\mu} \int_0^F x(F’) dF’}$$
パレート分布の期待値${μ = αxₘ/(α-1)}$を用いて計算すると、簡潔な結果が得られます
$${L(F) = 1 – (1-F)^{1-1/\alpha}}$$
つまり、最小値パラメータxₘの値に関係なく、αが同じであれば同じローレンツ曲線を持つのです。
パレート分布のジニ係数
さて、パレート分布のローレンツ曲線から、ジニ係数を計算してみましょう。
$${G = 1 – 2\int_0^1 L(F) dF}$$
$${= 1 – 2\int_0^1 [1 – (1-F)^{1-1/\alpha}] dF}$$
この積分を計算してみましょう。
$${G = \frac{1}{2\alpha – 1}}$$
先ほどもちょっと書きましたが、ジニ係数${G = 1/(2α-1)}$という関係式から、${α}$と不平等度の関係が明確になります
- α = 1.5のとき：${G = 1/(3-1) = 0.5}$（高い不平等）
- α = 2のとき：${G = 1/(4-1) = 0.33}$（中程度の不平等）
- α = 3のとき：${G = 1/(6-1) = 0.2}$（低い不平等）
- α → ∞のとき：${G → 0}$（完全平等に近づく）
観測データからαを推定することで、その現象の不平等度を直接的に評価できるというわけですね。
