ベータ分布についてわかりやすく解説｜二項分布との関わり

ベータ分布とは？

ベータ分布は、0から1の間の値を取る確率変数をモデル化するために用いられる連続確率分布です。

特に、割合や比率を表すような確率変数によく適合しますね。

例えば、

• コインを投げたときに表が出る確率
• ある製品の不良率
• あるイベントが発生する確率

などが挙げられます。

ベータ分布の確率密度関数

ベータ分布は、2つの正のパラメータ、αとβによって特徴づけられます。 確率密度関数f(x)は以下のように表されます。

$$f(x)=\frac{x^{\alpha -1}(1-x{)}^{\beta -1}}{B(\alpha ,\beta )}(0\le x\le 1)$$

ここで、B(α,β)はベータ関数と呼ばれるもので、以下の式で定義されます。

$$B(\alpha ,\beta )={\int }_0^1{t}^{\alpha -1}(1-t{)}^{\beta -1}dt$$

期待値

さて、期待値です。期待値は、ベータ分布でモデル化される現象における、ある事象が起こる確率の平均的な値を表します。

例えば、コイン投げで表が出る確率をベータ分布でモデル化する場合、期待値はコインの表が出る確率の平均的な値を意味します。

ベータ分布に従う確率変数 X の期待値は、パラメータ $\alpha$ と $\beta$ を用いて以下のように表されます。

$$E[X]=\frac{\alpha }{\alpha +\beta }$$

この式から、期待値は $\alpha$ と $\beta$ の比によって決まることがわかります。

$\alpha$ が $\beta$ より大きいほど、期待値は1に近づき、逆に $\beta$ が $\alpha$ より大きいほど、期待値は0に近づきます。

分散

さて、分散は期待値からのずれの大きさを表しますね。

分散が小さいほど、実際の確率は期待値の周辺に集中しており、予測が安定していると言えます。

ベータ分布の分散は、以下のように表されます。

$$Var[X]=\frac{\alpha \beta }{(\alpha +\beta {)}^2(\alpha +\beta +1)}$$

分散は、$\alpha$ と $\beta$ の値だけでなく、それらの和 $\alpha +\beta$ の値にも依存します。

一般的に、$\alpha$ と $\beta$ が大きくなるほど、分散は小さくなります。

期待値や分散についての詳細な説明は、こちらの記事をご覧ください。

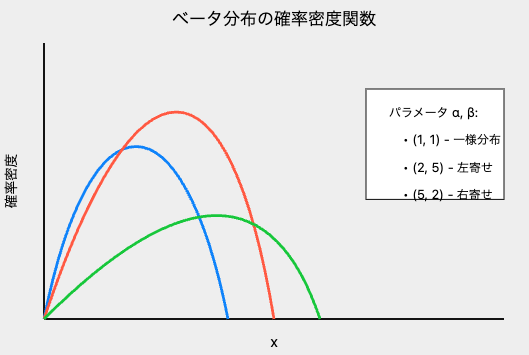
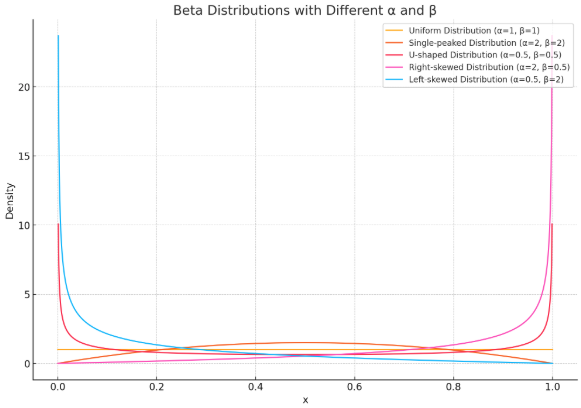
ベータ分布の形状

ベータ分布の形状は、パラメータ$\alpha$と$\beta$の値によって大きく変わります。

• $\alpha =\beta =1$ のとき、一様分布になります。
• $\alpha >1,\beta >1$ のとき、単峰な分布になります。
• $\alpha <1,\beta <1$ のとき、U字型の分布になります。
• $\alpha >1,\beta <1$ のとき、右に歪んだ分布になります。
• $\alpha <1,\beta >1$ のとき、左に歪んだ分布になります。

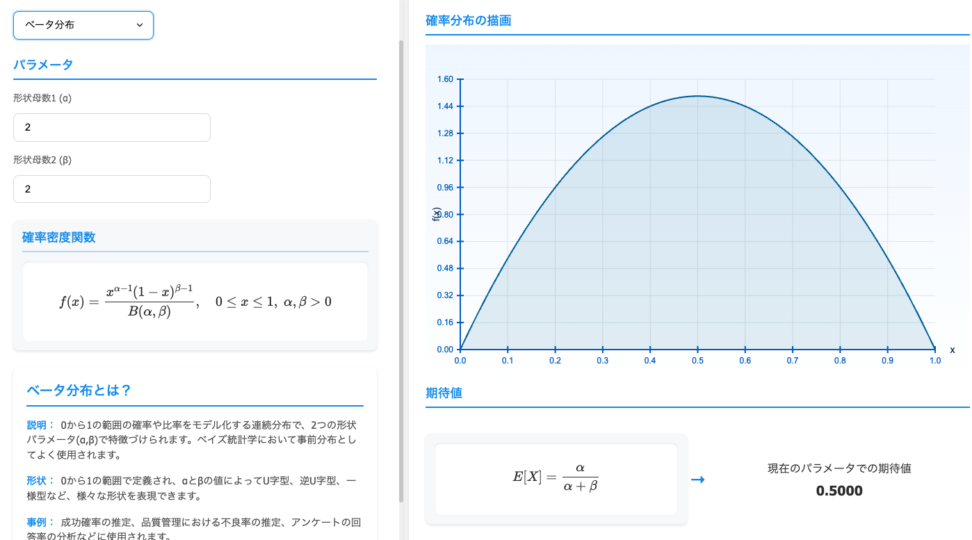
パラメータを自分で動かしたいという場合は、青の統計学-Ds Playground-の確率分布可視化ツールが便利です。

ぜひご覧ください。

確率分布可視化ツール｜ベータ分布

ベータ分布の他の確率分布との関係

二項分布との関係

ベータ分布は、二項分布の共役事前分布として知られています。

これは、ベイズ統計において、事前分布としてベータ分布を仮定すると、事後分布もベータ分布になることを意味します。

共役事前分布

ベータ分布が二項分布の共役事前分布であるということは、以下の関係式で表されます。

• 事前分布: $p(\theta )\sim Beta(\alpha ,\beta )$
  • $\theta$ は成功確率を表し、ベータ分布に従うと仮定します。
• 尤度関数: $p(X\mid \theta )\sim Binomial(n,\theta )$
  • $X$ は成功回数、$n$ は試行回数です。
• 事後分布: $p(\theta \mid X)\sim Beta(\alpha +X,\beta +n-X)$

ディリクレ分布との関係

ベータ分布は、多変量への拡張であるディリクレ分布の特殊な場合と考えることができます。

ベータ分布が1つのパラメータ（成功確率）の分布であるのに対し、ディリクレ分布は複数のパラメータ（例えば、カテゴリカルデータの各カテゴリの確率）の分布です。

ディリクレ分布の確率密度関数は以下のようになります。

$$p({\theta }_1,{\theta }_2,\dots ,{\theta }_K)=\frac{1}{B({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_K)}\prod _{i=1}^K{\theta }_i^{{\alpha }_i–1}$$

ここで、${\theta }_i$​ は$i$番目のカテゴリの確率、${\alpha }_i$​ は対応するディリクレ分布のパラメータです。

上記で説明した確率分布については、こちらでご覧ください。