パレートの法則についてわかりやすく解説
1. パレートの法則とは?
パレートの法則(Pareto Principle)は「全体の成果の80%が、全体を構成する要素の20%によってもたらされる」という経験則です。
現代では、ビジネス領域の「選択と集中」やマーケティング活動の優良顧客特定など、多くの分野でこの80/20の比率が使われています。
早速数学的背景から見ていきましょう!
ローレンツ曲線やジニ係数について勉強したい方はこちらをご覧ください。
ローレンツ曲線・ジニ係数・パレート分布をまとめて理解|不平等を数学で捉える
2. パレート分布とべき乗則:数学的背景
2.1 べき乗則 (Power Law) とは?
パレートの法則の背後にある数学的性質として、べき乗則 (Power Law) が役割を果たします 。べき乗則とは、ある変数 ${x}$ が「もう一方の変数をべき乗(冪乗)で表せる」という関係性です。具体的には、確率変数 ${X}$ がパレート分布に従う場合、その確率密度関数 (PDF) は次の形で表せます。
$${f(x) = \alpha \frac{x_m^\alpha}{x^{\alpha + 1}}, \quad x \ge x_m,\ \alpha > 0,\ x_m > 0 }$$
- ${\alpha}$ は「パレート指数 (tail index)」と呼ばれ、分布の「裾の重さ (heavy tail)」を決定するパラメータです。
- ${x_m}$ は分布が取り得る最小値(しきい値)です。
実は、パレート分布の形状パラメータが1の場合、パレート分布は指数分布に近似されます。
2.2 パレート分布と80/20
パレートの法則が「80/20」と表現されるのは、パラメータ ${\alpha}$ や ${x_m}$ の組み合わせによって、累積分布のある範囲に大きな割合が集中することに起因します。
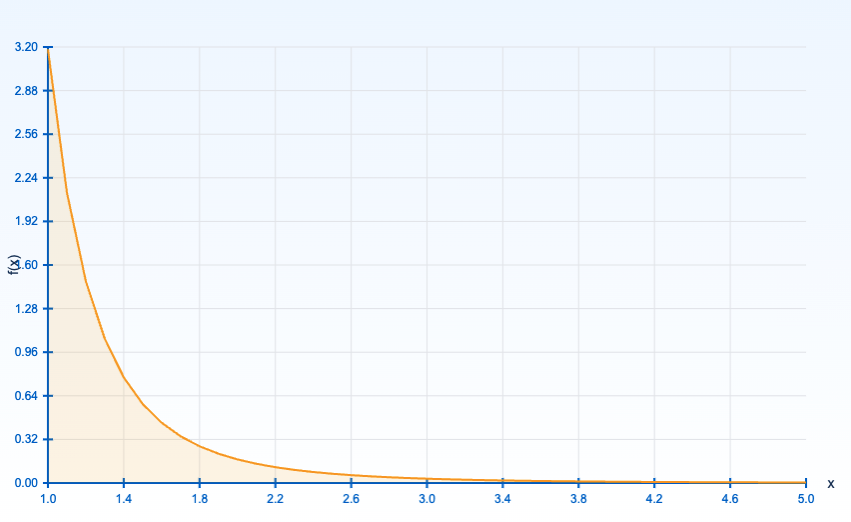
具体的には、所得分布・都市の人口分布・ウェブサイトのアクセス分布など多くの現象が「上位少数(20%前後)が全体に大きく寄与(80%前後)」という「極端な偏り」を持ちやすいのです
パレート分布の可視化は、DS Play groundを使うのがおすすめです。
3. ジップの法則・ロングテール
3.1 ジップの法則 (Zipf’s Law)
ジップの法則は、単語の出現頻度が順位のべき乗則に従うというもので、テキスト解析(自然言語処理)でよく知られています。
順位 ${r}$ と出現頻度 ${f(r)}$ の間に
$${f(r) \propto \frac{1}{r^s}}$$
のような関係が現れる 、つまり「1位の単語は2位の単語の約2倍使われる」といった振る舞いです。
これはパレート分布と同様に重い裾を持つ現象の一例であり、少数の単語が文章全体の頻出単語の大部分を占めるという意味で、パレートの法則に近い構造を持ちます。
3.2 ロングテール (Long Tail)
ロングテールは「売れ筋ではないマイナー商品」が大量に存在すると、その“総数”が決して無視できない売上になるという考え方です。
ECサイト(インターネット通販)などでは、上位商品の80%だけに依存せず、多様なニーズに対応することで利益を生む戦略が重要となります。これはパレートの法則とは対照的に、多数の細かな要素(下位80%)に注目する事例と言えます。
4. ビジネス応用:選択と集中 vs. ロングテール
ビジネスシーンでは、パレートの法則を活用して「顧客」「商品」「事業領域」のうち、特に重要な20% を見極めることがよく行われます 。例えば以下のような例が典型です。
- 売上の80% は、20%の商品や顧客群から得られている
- クレーム原因の80% は、20%の問題点や製品仕様に集中している
- アクセス数の80% は、サイト内の20%のページに集中している
一方で、この「20%にだけ注力する」戦略を過度に推し進めると、ロングテールが潜在的に持つ価値を見落とすリスクがあります。組織運営においても、常に「上位20%」の人材のみを重視すると、残りの80%のモチベーションを下げる恐れがあります (参考文献 [15])。

したがって、80/20を“絶対視”するのではなく、状況に応じてロングテールとのバランスを検討することが重要です。
5. パレートの法則を用いたデータ分析事例
ここでは、ウェブサイトへのアクセスログを分析し、パレートの法則を可視化する具体的な手順を示します。
5.1 パレート図 (Pareto Chart) の作成フロー
- アクセスログの収集
サーバーのアクセスログを取得し、ページ別アクセス回数を集計する。 - アクセス数の多い順に並び替え
ページ毎のアクセス数が高い順にソートする。 - 累積アクセス割合を計算
上位何%のページが、全体アクセスの何%を占めているかを算出する。 - パレート図を作成
縦軸に「アクセス数」および「累積割合」、横軸に「ページの順位」をとった図を描き、上位20%が全体のアクセスの80%前後を占めるかを視覚的に判断する。
5.2 Pythonを使った例
以下に、Pythonでパレート図(簡易版)を作成するサンプルコードを示します。実運用では、ログ解析ライブラリや可視化ライブラリを組み合わせてさらに高度な分析が可能です。
import numpy as np
import matplotlib.pyplot as plt
# ===== 1. ダミーデータの生成(ページ別アクセス数) =====
# 仮に100ページあり、パレート分布っぽいアクセス数を生成してみる
np.random.seed(42)
alpha = 2.0 # パレート指数(例)
x_m = 1.0 # 最小値
num_pages = 100
# パレート分布に従う乱数を生成
# X ~ Pareto(alpha, x_m)
# X = x_m * (1 - U)^( -1/alpha ), Uは一様乱数
U = np.random.rand(num_pages)
access_counts = x_m * (1 - U)**(-1/alpha)
# 整数に丸める(実際のアクセス数を仮定)
access_counts = np.round(access_counts * 100).astype(int)
# ===== 2. 多い順に並び替え =====
sorted_counts = np.sort(access_counts)[::-1]
# ===== 3. 累積アクセス割合を算出 =====
cumulative_counts = np.cumsum(sorted_counts)
total_access = cumulative_counts[-1]
cumulative_ratio = cumulative_counts / total_access
# ===== 4. パレート図を作成 =====
plt.figure(figsize=(10, 6))
plt.bar(range(num_pages), sorted_counts, color='skyblue', label='アクセス数(ページ別)')
plt.plot(range(num_pages), cumulative_ratio * max(sorted_counts), color='red', marker='o', label='累積割合')
plt.xticks(range(0, num_pages, 10), rotation=45)
plt.xlabel('ページ順位')
plt.ylabel('アクセス数')
plt.title('パレート図の例(アクセス数)')
plt.legend(loc='upper right')
plt.grid(True)
plt.show()このように、データの上位20%が全体のアクセスの80%前後を占めるかどうかを一目で把握できます。もし実際に80/20に近い形状が確認できれば、上位のページを重点的に改善することにより、効率的にサイト全体のパフォーマンスを底上げできる可能性があります
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!


