コーシー分布とは？わかりやすく解説

1. コーシー分布とは？ざっくり解説

はじめに、コーシー分布は「重い裾(fat-tail)を持つ分布」として知られ、平均や分散が定義できないという面白い特徴を持っています。

確率論を学ぶと真っ先に登場する正規分布とは異なり、外れ値が頻繁に出現しうる分布です。

そんなユニークな分布な分布をご紹介します。

基本的な前提知識をおさらいしたい方は、こちらをどうぞ

連続確率分布の一種であるコーシー分布は、

の2つで定義されます。確率密度関数は次の式で表されます。

$${f(x; x_0, \gamma) = \frac{1}{\pi \gamma \left[ 1 + \left(\frac{x – x_0}{\gamma}\right)^2 \right]}}$$

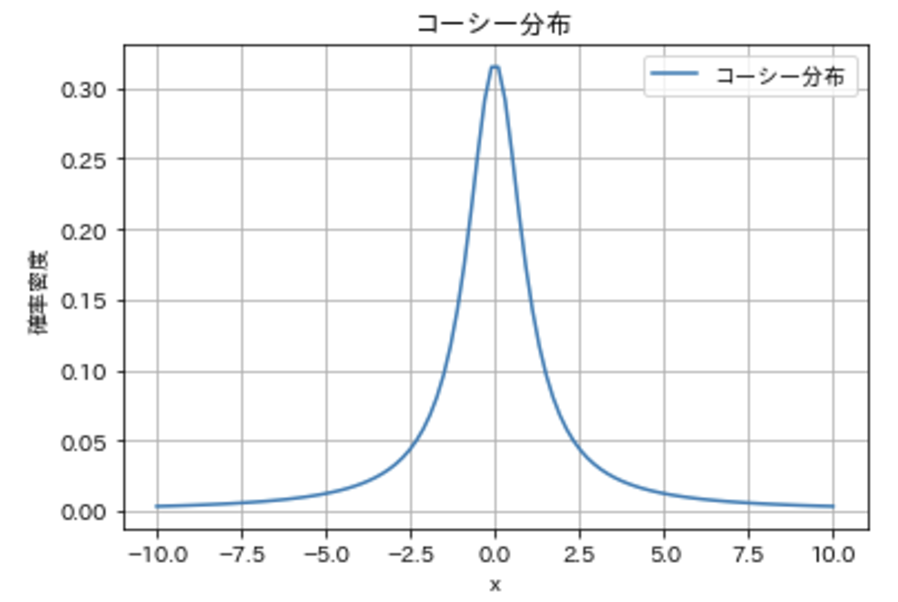
特に${x_0 = 0, \gamma = 1}$のときは「標準コーシー分布」と呼ばれ、これがコーシー分布の代表的な形になります。

確率分布を特徴づける道具として有名なのが、特性関数 と モーメント母関数です。

通常、多くの分布(正規分布やポアソン分布など)はモーメント母関数を用いて分布の性質を解析します。

コーシー分布にはモーメント母関数(MGF)が存在しない(厳密には定義域が限られている)ため、解析には特性関数が主に使われます。標準コーシー分布の特性関数${\phi(t)}$は以下のように求められます。

$${\phi(t) = E[e^{itX}] = e^{-|t|}}$$

これはほかの分布にはない興味深い性質で、指数関数的に減衰する形を取っています。

しかも、${|t|}$という絶対値が効いていることがコーシー分布の重さと関係しています。

一般的に、モーメント母関数${M_X(t) = E[e^{tX}]}$は確率分布の平均や分散を導出する際に用いられます。

ところが、コーシー分布の場合は積分が収束せず、通常の意味ではモーメント母関数を定義できません。

これが「平均・分散が存在しない」という事実と結びつきます。

コーシー分布は、その分布特性上、モーメント(例えば平均や分散に対応する1次・2次モーメント)が収束しないことで知られています。なぜ収束しないかというと、裾が極端に重いからです。

通常の分布（例えば正規分布）では、確率密度関数が指数関数的に減衰するため、${\int_{-\infty}^{\infty} x^2 などの積分が有限になります。
コーシー分布は重い裾を持つため、${\int_{-\infty}^{\infty} |x| f(x) dx}$でさえ無限大となり、平均(1次モーメント)も分散(2次モーメント)も有限値に収束しません。

このような性質があるため、コーシー分布を用いた解析では、平均や分散に頼らない指標を用いる必要があります。

たとえば「中央値」や「四分位範囲(IQR)」が注目されることも多いです。

さて、ここまでで最低限抑えて欲しいのは、以下のような正規分布との差分です。

コーシー分布は安定分布(stable distribution)の一種です。

安定分布は、独立な同じ分布に従う変数の和が元の分布のスケーリング・シフト版になるような分布を指します。正規分布も安定分布の一種ですが、コーシー分布は安定パラメータ${\alpha = 1}$の特別なケースとして位置づけられます。

安定分布の一部であるということは、ある意味で「自己相似性」を持つということです。

コーシー分布のように外れ値が頻出する状況を扱うには、平均や分散を信頼できないため、ロバストな推定がだいじになります。

コーシー分布の理論は以下のような示唆を与えます。

最小二乗法が破綻する例
外れ値を含むデータを最小二乗法(OLS)で解析すると、極端な値が平均を引っ張ってしまい、推定結果が大きく歪められることがあります。
ロバスト損失関数の利用
コーシー分布をヒントにしたコーシー損失関数などを採用することで、外れ値の影響を抑えた推定が可能になります。