ガンマ分布とは?リスク解析と保険数理に使える分布
ガンマ分布とは
ガンマ分布とは、連続型の確率分布の一種で、主に「待ち時間」や「寿命」「損害額」などのモデリングに広く使われる分布です。その汎用性の高さが特徴的です。

イベントが起こるまでの時間や機械・部品の寿命を表すモデルとしてよく利用されます。指数分布(後述)を一般化した形でもあり、さまざまな形状をとることができる柔軟性が魅力です。
ガンマ分布はふたつのパラメータ(しばしば形状パラメータ${\alpha}$と率パラメータ${\beta}$ などと表記されます)によって定義され、その確率密度関数は以下のように書かれます。
$${f(x; \alpha, \beta) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha – 1} e^{-\beta x} \quad (x > 0, \; \alpha > 0, \; \beta > 0)}$$
${\Gamma(\alpha)}$はガンマ関数と呼ばれる特殊関数で、ガンマ分布の名前の由来にもなっています。
ガンマ分布の可視化は、青の統計学-DS Playground-の確率分布可視化ツールが便利です。
ぜひご覧ください。
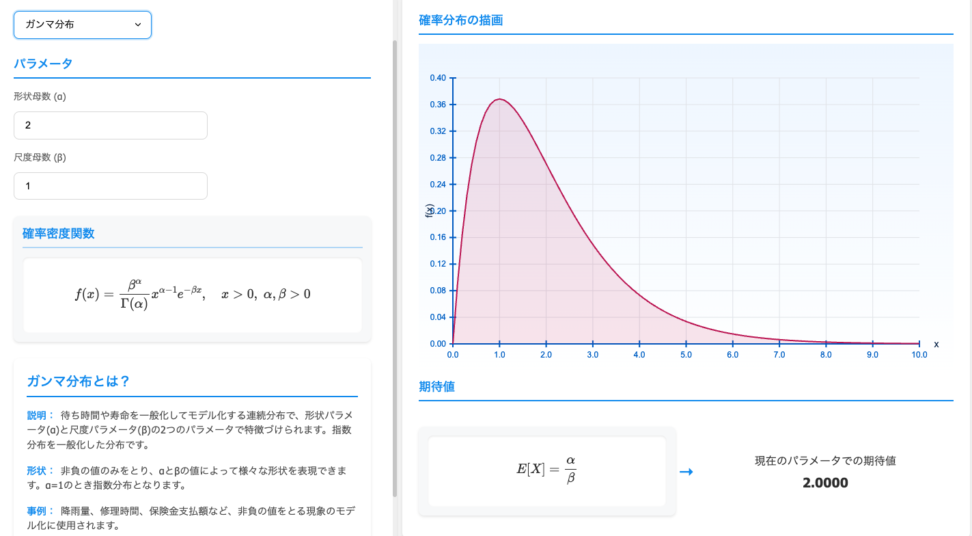
こちらをクリックすると、ガンマ分布のページに飛びます。
ガンマ分布の基本的な性質
ここでは、ガンマ分布の代表的な性質をいくつか挙げます。
- 期待値と分散
- 期待値: ${E[X] = \frac{\alpha}{\beta}}$
- 分散: ${\mathrm{Var}(X) = \frac{\alpha}{\beta^2}}$
- 形状の柔軟性
形状パラメータ${\alpha}$が1未満、1付近、1を超える場合とで、確率密度関数の形が大きく変化します。- 実は、指数分布は形状パラメータ${\alpha = 1}$の特殊なガンマ分布にあたります。

指数分布は「待ち時間」を表す分布として最も基本的ですが、ガンマ分布はこの単純なモデルを拡張したものといえます、
再生性
同じ率パラメータ${\beta}$を持つガンマ分布同士を足し合わせると、形状パラメータが和になるガンマ分布となる性質があります。
すなわち、ガンマ分布 ${Ga(\alpha_1,\beta)}$に従うあるデータと、そのデータとは独立なガンマ分布 ${Ga(\alpha_2,\beta)}$に従うデータを足したデータは、以下のようなガンマ分布 に従います。
$${Ga(\alpha_1+\alpha_2,\beta)}$$
これにより、複数の指数分布を合成した分布として解釈できるのも特徴です。
正規分布とかポアソン分布も同じ性質ですね。
ガンマ分布とカイ二乗分布の関係
ガンマ分布は多くの有名な確率分布と密接な関係がありますが、χ²(カイ二乗)分布との関係を語ります。
カイ二乗検定や分散分析でよく用いられるため、ガンマ分布は広範な分野とつながっていますね
さて、カイ二乗分布はガンマ分布の特別なケースです。
自由度${k}$のカイ二乗分布は、形状パラメータ${\alpha = k/2}$、率パラメータ${\beta = 1/2}$のガンマ分布と等価になります。
この関係性から、カイ二乗分布もガンマ分布の性質をいくつか継承しています。例えば、独立なカイ二乗分布に従う確率変数の和は、再びカイ二乗分布に従います。
これは、ガンマ分布の合成性から導かれますね
具体例|保険数理におけるガンマ分布の応用
さて、保険会社における損害額のモデル化をしてみます。
実際の保険商品設計では、再保険契約や年間累積損害(アグリゲート)の取り扱いも考慮するケースが多いので、以下の例よりはもう一段階複雑になる気がします。
- 損害額のモデル
- 損害額 ${X}$をガンマ分布 ${\mathrm{Gamma}(\alpha, \theta)}$で近似しましょう。
- 形状パラメータを ${\alpha}$、尺度パラメータを ${\theta}$とし、確率密度関数は次のようになりますね。
- ${f_X(x) = \frac{1}{\Gamma(\alpha)\,\theta^\alpha} x^{\alpha – 1} e^{-x/\theta} \quad (x > 0)}$
実際には、過去の支払損害データから最尤推定などの手法を用いて${\alpha}$と${\theta}$を推定します。
ここでは例として、過去データを分析した結果、
- ${\hat{\alpha} = 2.0}$
- ${\hat{\theta} = 20000 \text{円}}$
と推定できたとします。

形状パラメータが2、平均損害額が ${\alpha \times \theta = 40000}$円というイメージです
- 免責金額(デダクティブル)の設定
- 車両保険などでは、事故時の損害額の一部を自己負担として定める場合があります。これを免責金額(デダクティブル)といいます。
- ここでは免責金額を ${\mathrm{D} = 50{,}000}$円と設定します。つまり、損害額${X}$が 5万円以下の場合は保険金の支払いがなく、5万円を超えた場合はその超過部分だけを支払います。
今回の目的って何?
この保険設計において、1契約あたりの期待損害額(純保険料)を求めることが目的です。この純保険料は、実際の保険料算定時に付加保険料(事業費や利益など)を上乗せする前の基礎的なコストを意味します。
期待損害額の計算方法
損害額を ${X}$とし、免責金額 ${\mathrm{D}}$ のもとで保険会社が支払う保険金を${Y}$ とすると、
$${Y = \begin{cases} 0, & X \le \mathrm{D} \\ X – \mathrm{D}, & X > \mathrm{D} \end{cases}}$$
となります。
このときの期待値 ${E[Y]}$は、以下の式で求められます。
$${E[Y] = \int_{\mathrm{D}}^{\infty} (x – \mathrm{D}) f_X(x)\, dx}$$
この辺は、期待値の定義通り計算をやっているだけなので、いかつい見た目に騙されないようにしてください。
ガンマ分布の確率密度関数 ${f_X(x)}$を代入して積分すると、不完全ガンマ関数などを用いて解析的に求めることも可能ですが、実務では手計算する人はいないです。数値積分や統計ソフトを使って計算するのが一般的です。
仮計算例
ここでは、
- ${\hat{\alpha} = 2.0}$
- ${\hat{\theta} = 20000}$
- ${\mathrm{D} = 50000 }$
のときに、数値例を簡単に示してみます。
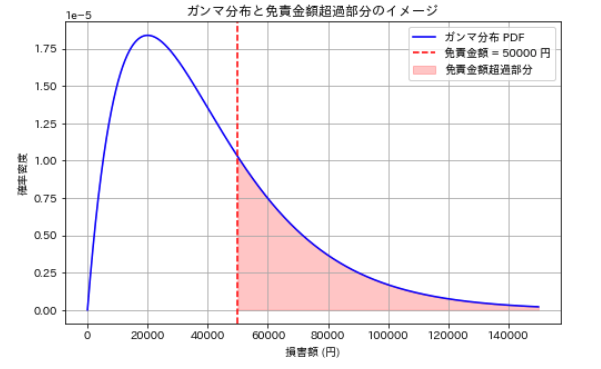
免責金額 50000 円以上の保険金支払の期待値: 7387.65 円

可視化させてみました。ガンマ分布の形状や免責金額を超える部分の領域が可視化されるとともに、免責金額超過部分の期待支払額が数値として確認できます。
- 分布の概要
- 平均損害額: ${\hat{\alpha} \times \hat{\theta} = 2.0 \times 20000 = 40000}$円
- 損害額が 0 円から数十万円程度の範囲に広がる可能性を想定。
- 期待損害額の計算
- 免責金額 5万円を超過する部分のみ支払うため、5万円以下の損害に対しては保険金支払いはありません。
- 計算結果、${E[Y] \approx 20{,}000 \text{円}}$円 と試算できたとします
結果の解釈
- 1契約あたり、損害コストとして平均約2万円が見込まれると分かりました。
- 実際の保険料を設定する際には、この金額に保険会社の事業費やリスクヘッジのためのローディングを加算して総保険料(純保険料 + 付加保険料)を算定します。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!






