【深層生成モデル】VAEの仕組みをわかりやすく解説｜ベイズ統計
こんにちは、青の統計学です。
今回は、深層生成モデルのVAEについて解説いたします。
ノイズに頑健な深層生成モデルとして、画像生成モデルとして利用されているので、生成AIの利用が広まってきた今勉強する価値ありです！
VAE｜Variational Autoencoder
VAEは変分オートコーダの略です。
端的にいうと、VAEはオートエンコーダで求める潜在変数が確率分布（標準正規分布）に従うと考える点が特徴です。
これにより、以下のようなメリットがあります。
正則化（Regularization）
VAEは潜在空間に確率分布を導入し、その分布を正則化します。
これにより、過学習を防ぐ効果があります。
潜在空間の連続性と平滑性
VAEの潜在空間は確率分布に基づいているため、より連続的で平滑です。
これにより、新しいデータや中間データを生成する際に、より滑らかな遷移を実現できます。
とはいえ、仕組みを理解しないと仕方がないのでオートエンコーダーから見てみましょう。
auto encoder とは
VAEについて理解する前にオートエンコーダについて理解しましょう。
オートエンコーダーは、主に次元削減や特徴抽出のために使用される、ニューラルネットワークの一種です。
オートエンコーダーの基本的な目的は、入力をエンコード（圧縮）し、その後で元の入力にできるだけ近い形でデコード（復元）することです。
このプロセスは、入力データの重要な特徴を学習するのに役立ちます。
オートエンコーダーは大きく分けて2つの部分から構成されます：
- エンコーダー（Encoder）：
- 入力データを内部表現（潜在空間表現）に変換します。
- この部分は通常、次元削減を行うために、入力層から出力層に向かって徐々にユニット数が減少するような構造を持ちます。
- デコーダー（Decoder）：
- 内部表現から元の入力データを再構築（再構成）しようと試みます。
- エンコーダーの逆の構造を持ち、出力層に向かって徐々にユニット数が増加します。
以下の図のように、エンコーダとデコーダに構造が分かれています。
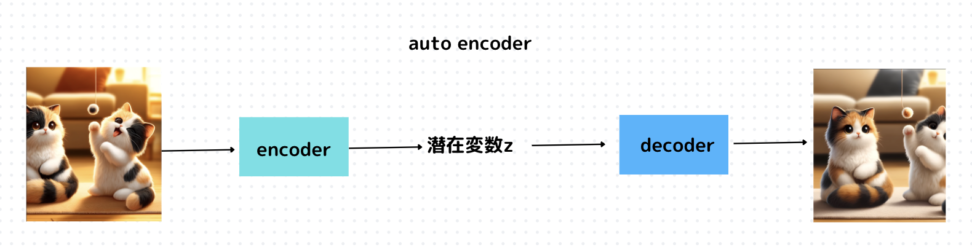
つまり入力データ\(X\)から潜在変数\(z\)に変換するニューラルネットワークをエンコーダと呼び、逆に潜在変数をインプットとして元画像を復元するニューラルネットワークをデコーダと呼んでいます。
→そもそものモチベーションは、次元削減など、画像のデータの特徴量が潜在変数に埋め込まれて欲しいからですね。
$$\hat{x}(x) = \hat{f}(\hat{W} f(Wx+b)+\hat{b}$$
ニューラルネットワークの仕組みは上のように非線形変換を通します、
$$Loss = \sum_{n=1}^N \|x_n – \hat{x}(x_n) \|^2$$
これは再構築誤差（reconstruction error）と呼びます。
誤差逆伝播法で、この損失を小さくするような\(w\)を探索します。
ここまでの内容は以下のコンテンツでも同様に取り扱っています。
数学的背景
さて、冒頭でオートエンコーダで求める潜在変数に標準正規分布を仮定するというのがVAEの特徴とお話ししました。
潜在変数の確率分布\(p(z)\)と、その分布からサンプリングされた\(Z\)から\(X\)がサンプリングされる条件付き確率\(p(X|Z)\)を作ることで、潜在変数を元にしたサンプリングを行います。
モデルは以下のように、潜在変数\(z\)が標準正規分布であることが仮定されています。
一方、\(x_n\)もNNで期待値が計算されています。（ここは実装次第なので話半分でOK）
$$p(x_n,z_n)=\prod_{k}N(x_{n,m}|f_m(z_n,\theta),1)$$
$$p(z)=\prod_{k}N(z_{n,k}|0,1)$$
先ほど、エンコーダとデコーダの話をしましたが、より数理的に解釈すると
データ\(X\)から潜在変数\(z\)を対応づけるニューラルネットワークをEncoderと呼び、潜在変数\(z\)からデータ\(X\)を復元するニューラルネットワークがDecoderです。
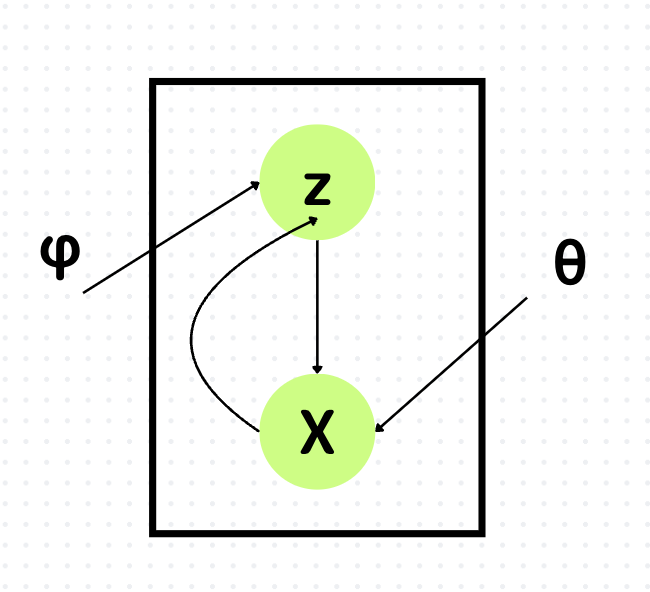
\(\phi\)はEncoderのパラメータ、\(\theta\)はDecoderのパラーメータです。
ポイントは、Encoderは直接\(z\)を生成するのではなく、下記のように\(z\)が従う正規分布のパラメーター\(\mu , \sigma\)を生成していることです。
\(x\)の分布から\(z\)をサンプリングするといったものの、サンプリング自体は確率的なので、微分ができず、誤差逆伝播法が使えないです。
→層を厚くしても学習の旨みがない。
なので、\(x\)から\(z\)を出力するときに、\(x\)の分布の統計量を使って変換を行います。
以下のようなイメージです。
\(z \sim N(\mu(X), \sigma(X))\)を直接扱うのではなく,\(\epsilon〜N(0,I)\)のもと、
$$z = \mu(X) + \epsilon*\sigma(X)$$
のように、確率変数を避けて、誤差逆伝播法を適用することができます。
これをreparametarization trick と呼びます。
さて、パラメータ推定は事後分布を考えます。
このように、データ\(X\)の平均と分散を所与にした正規分布に従うように、潜在変数の事後分布を近似させていきます
$$p(z|x)=\prod_{k}N(z_{k}|μ_{k}(x,\phi),\sigma_{k}(x,\phi))$$
事後分布の近似に何を使うかというと変分下界を使います。
変分下界について
なので！以下のような変分下界を最大化するパラメータを推定します。
$$B(\theta,\phi)=\int q_{\phi}(z|x)log \frac{p_{\theta}(x,z)}{q_{\theta}(x|z)}$$
$$B(\theta,\phi)=E_{q_{\phi}(z|x)}[log p_{\theta}(x|z)]-D(q_{\phi}(z|x)||p(z))$$
見覚えのある形が出てきたかと思います。
第1項はクロスエントロピーで、第二項はKLダイバージェンスですね。
KLダイバージェンスについては、以下のコンテンツをご覧ください。
第1項が\(log p(X)\)の下界になっておりますね。
第2項が事後分布と元々仮定していた標準正規分布をどれだけ離れているかの指標なので、上の式を最大化するとパラメータを推定できそうです。
もう少し掘り下げると、以下のような役割です。
第1項
\(X\)があって，分布\(q\)によって\(z\)に変換したものを，分布\(p\)で\(x`\)に変換される確率を高める役割です。
→前述した復元誤差についての項(復元誤差を小さく）
第2項
どんな\(y\)から分布のによって得られる\(z\)の分布も，\(p(z)\)に近づける役割です。
→潜在変数\(z\)の分布を保証するため
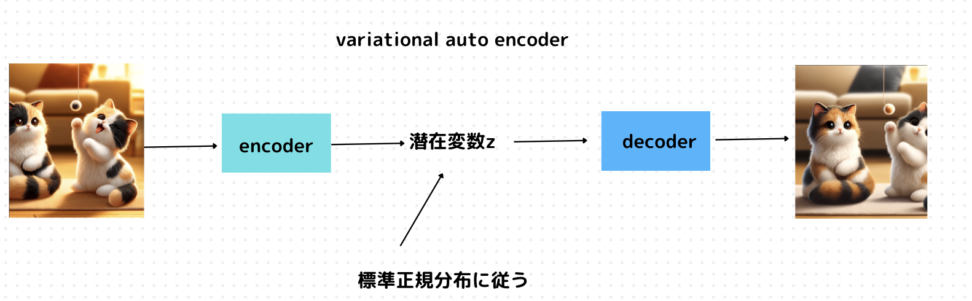
VAEの面白い点としては、教師データのない教師なし学習にもかかわらず同じクラスラベルのデータが近いところに集まることです。
VAEは潜在変数が正規分布に従うように設計されており、正規分布に従う乱数を学習時に取り入れているので、この乱数によるブレによって似た形状のものを近くに寄せる効果があります。
つまり、同じ画像を入力しても毎回少しずれたところに潜在変数がプロットされ、その潜在変数からデコーダによって生成する画像を入力画像と同じようにします。
補足 ：変分下界によるパラメータ推定の限界について
この変分下界を使った型のVAEには限界があります。
以下の論文では、その原因と対策を論じています。
https://arxiv.org/pdf/1706.02262.pdf
デコーディング分布\(p(x|z)\)の表現力が高い場合、精度が下がる傾向にある
デコーディング分布は潜在変数zが与えられたときに観測データxがどのように生成されるかをモデル化する条件付き確率分布\(p(x|z)\)です。
補足：一方、\(p(z|x)\)はエンコーディング分布（あるいは推論分布）と呼ばれ、観測データ\(x\)が与えられたときの潜在変数\(z\)の分布を表します。
表現力が高いデコーディング分布とは、デコーダ部分が非常に表現力が高く、複雑なデータパターンをモデル化する能力がある状況を指します。
デコーダがこのように柔軟な場合、モデルは入力データを再構築する際に潜在変数をあまり活用しなくなることがあります。
これは、デコーダが単独でデータの複雑な分布を学習し、再現する能力を持っているため、潜在変数からの情報がそれほど重要ではなくなるためです。
この結果、VAEは潜在空間の特徴を無視し、潜在変数とデータ間の有意義な関係を学習しなくなる可能性があります。
言葉だけだと難しいので、先ほどの変分下界の式を見て見ましょう。
$$B(\theta,\phi)=E_{q_{\phi}(z|x)}[log p_{\theta}(x|z)]-D(q_{\phi}(z|x)||p(z))$$
第1項は、デコーダによるデータの再構築能力を示しており、デコーダの表現力が高ければ高いほど、この項の値は大きくなります。
つまり、潜在変数\(z\)から観測データ\(x\)をうまく再現できる能力が高いことを意味します。
デコーダが高い表現力を持つと、第一項が増加しますが、同時にモデルが複雑になりすぎると過学習のリスクがあり、第二項に影響を及ぼす可能性があります。
このバランスを取ることが、VAEのモデル設計と学習の重要な側面です。
