【時系列】状態空間モデルをわかりやすく解説|カルマンフィルタの仕組み
こんにちは、青の統計学です。
今回は、状態空間モデルについて解説いたします。

大学で統計学を学ぶと、多くの場面で観測データから母数を推定するという枠組みに出会います。しかし、現実の世界では、推定したい対象自体が時間の経過とともに刻一刻と変化し、しかもその変化自体にノイズが含まれていることが少なくありません。
例えば、株価などがわかりやすいですかね。
こうした動的に変化するシステムを記述し、不完全な観測から真の状態を推定するための強力なフレームワークが状態空間モデルであり、その代表的な推定アルリズムがカルマンフィルタです。
MMMと並び広告効果の予測に使われたりと実務での応用も可能な時系列モデルですが、チューニングや実装の難易度が高いという点もあります。状態の概念から詳しく解説していきます。
状態空間モデルの数学的表現
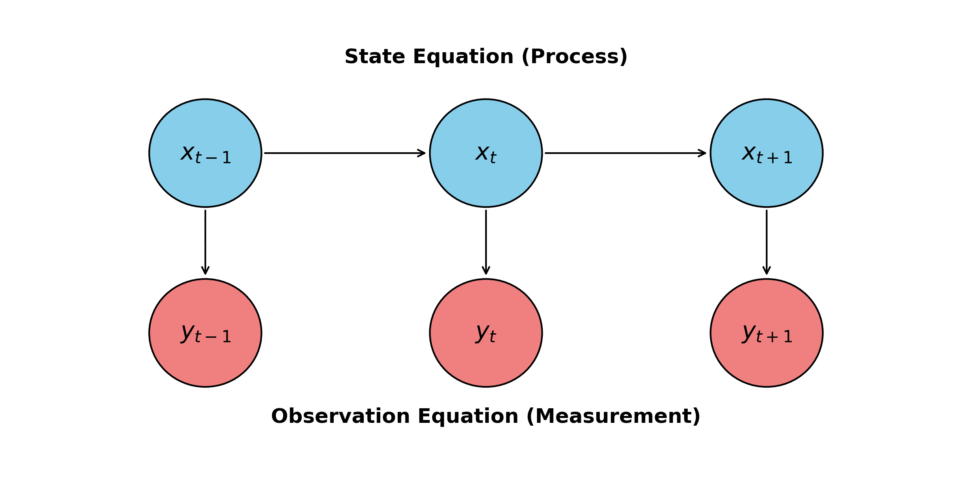
状態空間モデルの核心は、私たちが直接見ることのできない「状態」と、それを通じて得られる「観測」を分けて考えることにあります。この二つの関係を記述するために、以下の二つの方程式を用います。
「状態」って何??
まずは、状態の概念から理解しましょう。
下の図のように、時刻nまでのデータが手元にあると考えます。
\(n\)が現在なので、現在と過去が張る空間が左側になります。
そして、我々が解きたい問いは「将来の予測をする」なので、右側が将来と現在\(n\)が張る空間です。
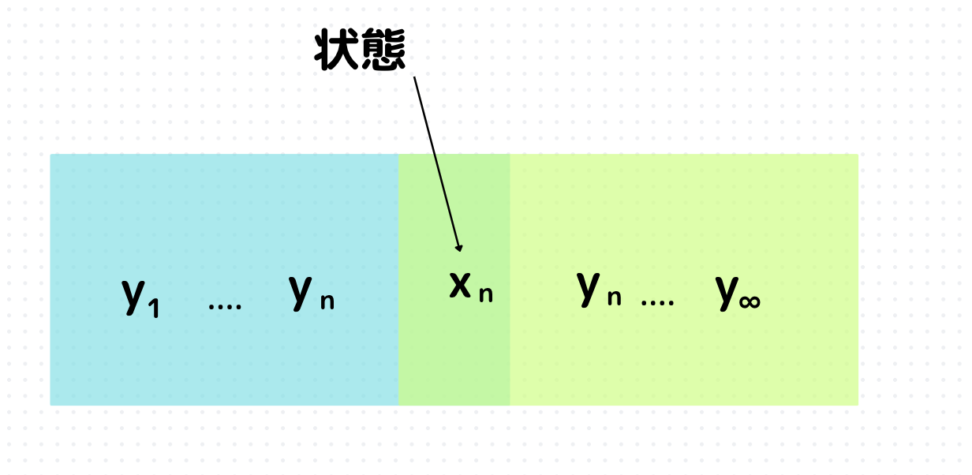
状態とは、時刻nまでの情報のうち、そのモデルが将来の予測に必要な情報を集約したもの、です。
下は1次のARモデルなので、1期前のデータしか必要ないので状態\(x_n\)については、以下のようになります。
$$x_n=y_n$$
システム方程式(状態方程式)
状態が時間の経過とともにどのように遷移するかを記述します。
これは、直接観測できない状態\(x_n\)がどのように時間変化するのかを表現するモデルです。
$${x_t = F_t x_{t-1} + w_t}$$
- $x_t$ は時刻
- $t$ における真の状態
- $F_t$ は状態遷移行列
- $w_t$ はシステムノイズ(プロセスノイズ)
システムノイズは通常、平均0、分散 $Q_t$ の正規分布 $N(0, Q_t)$ に従うと仮定されます。
観測方程式
「見えない状態」が、どのような形で「見えるデータ」として現れるかを記述します。
$${y_t = H_t x_t + v_t}$$
- $y_t$ は時刻 $t$ における観測値
- $H_t$ は観測行列
- $v_t$ は観測ノイズ
- 観測ノイズも同様に、平均0、分散 $R_t$ の正規分布 $N(0, R_t)$ に従うと仮定されます。
観測モデルが回帰モデル、そして状態が回帰係数、そしてシステムモデルが回帰係数がどう変化するのかを表現したモデルとして扱われます。

つまり、状態空間モデルとは「マルコフ性(現在の状態は直前の状態にのみ依存する)」を持つ状態の連鎖と、そこから発生する観測データの二階層構造を持つモデルなのです。
ベイズ推定の視点:カルマンフィルタ
カルマンフィルタを理解する上で重要な視点は、それが逐次ベイズ推定の特殊なケースであると捉えることです。
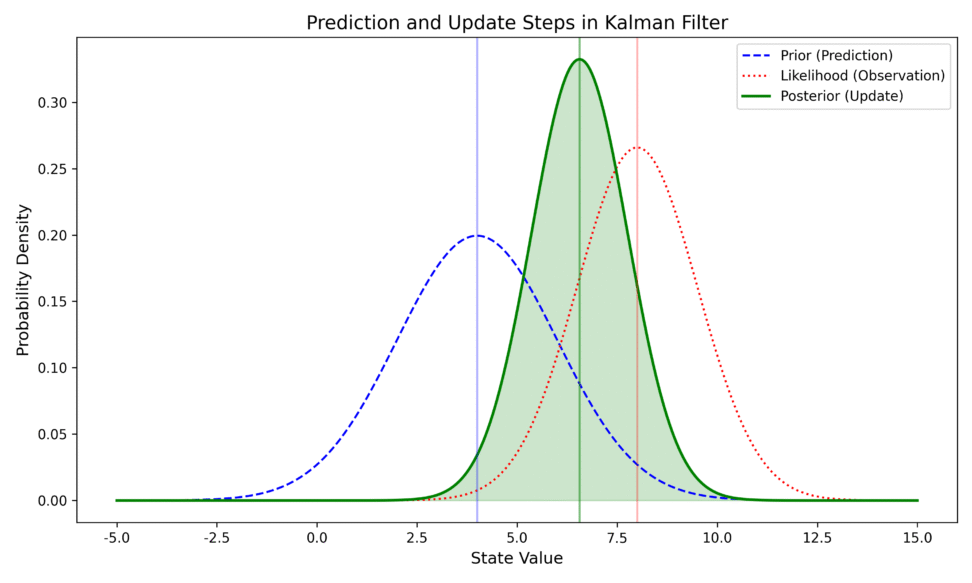
ベイズ統計学の基本的な考え方は、「新しいデータを得るたびに、対象に関する確信(分布)を更新していく」というものです。カルマンフィルタは、この更新を予測と更新という二つのステップの繰り返しで実現します。
- 予測ステップ(Prediction): 直前の状態の推定値から、現在の状態がどうなっているかを「予測」する。
- 更新ステップ(Update): 実際に得られた観測データを使って、予測を「修正」する。
なぜ「正規分布」なのか
カルマンフィルタが実用的な理由は、すべてのノイズと初期状態に正規分布(ガウス分布)を仮定している点にあります。
正規分布には、再生性という性質がありまして、正規分布に従う変数同士を足し合わせたり、線形変換したりしても、結果はやはり正規分布になります。これにより、複雑な積分計算をすることなく、平均(期待値)と分散という二つのパラメータを追いかけるだけで、事後分布を完全に記述できます。
カルマンフィルタの仕組みについて
カルマンフィルタの手順は、大きく分けて「予測フェーズ」と「更新フェーズ」にわかれます。
予測フェーズは一期先の条件付き期待値と条件付き分散の予測を状態方程式をもとに行い、更新フェーズではデータを更新します。
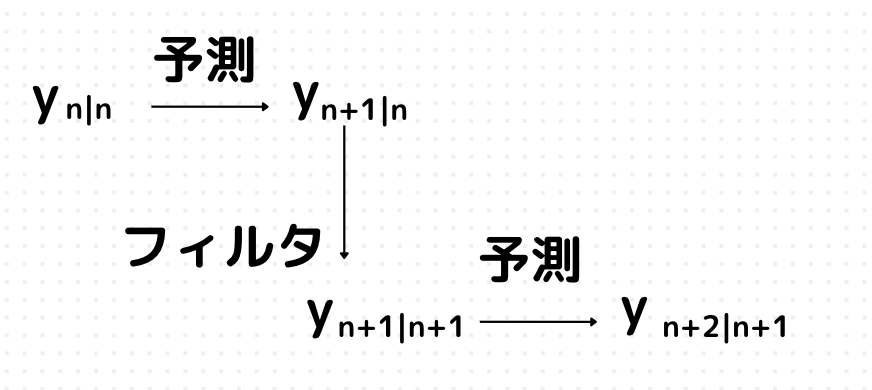
データをもとに更新というのは、上で言うと\(y_{n+1|n}\)で\(n+1\)時点でデータの予測をしていましたが、実際のデータ\(y_{n+1}\)を与えると言うことです。
予測ステップ
まず、前時刻の推定値(事後分布)を用いて、現時刻の状態を予測します。
これを「事前分布」と呼びます。
前提となるシステムモデル
まずは、対象となるシステムの動きと、観測の仕組みを数式で定義します。
$$ \begin{aligned} x_t &= F_t x_{t-1} + w_t \\ y_t &= H_t x_t + v_t \end{aligned} $$
- $x_t$ (状態変数):推定したい真の値(位置や速度など)
- $y_t$ (観測変数):センサ等から実際に得られる値
- $F_t$ (状態遷移行列):前の状態から次の状態へどう変化するかを表すモデル
- $H_t$ (観測行列):状態がどのように観測値として現れるかを表すモデル
- $w_t, v_t$ (ノイズ):システムノイズ(共分散 $Q_t$)と観測ノイズ(共分散 $R_t$)
- これらは正規分布に従うホワイトノイズと仮定します。
状態の予測
物理法則などのモデル($F_t$)に基づいて、次の状態を予測します。
$$\hat{x}_{t|t-1} = F_t \hat{x}_{t-1|t-1}$$
不確実性の予測
予測に伴う「自信のなさ(誤差共分散)」を計算します。
$$P_{t|t-1} = F_t P_{t-1|t-1} F_t^T + Q_t$$

ここで注目すべきは、右辺の $+ Q_t$ です。不確実性(分散) $P$ がシステムノイズ $Q$ によって増大しています。これは、観測を行わずに予測だけを続けていると、時間が経つほど推定に自信がなくなっていくことを意味しています。
更新ステップ
次に、実際に得られた観測値 $y_t$ を用いて、予測値(事前分布)を修正し、最終的な推定値(事後分布)を求めます。 この時、予測と観測のバランスを調整する係数がカルマンゲイン ($K_t$)です。
- カルマンゲインの計算
- $ K_t = P_{t|t-1} H_t^T (H_t P_{t|t-1} H_t^T + R_t)^{-1} $
- 状態の更新
- $ \hat{x}_{t|t} = \hat{x}_{t|t-1} + K_t (y_t – H_t \hat{x}_{t|t-1}) $
- 不確実性の更新
- 観測によって情報が得られたため、不確実性は減少します。
- $P_{t|t} = (I – K_t H_t) P_{t|t-1} $
更新ステップの「状態の更新式」をよく見てみましょう。
$$ \text{新しい推定値} = \text{予測値} + K_t \times (\text{観測値} – \text{予測値}) $$
これは「予測値」に「観測値と予測値のズレ(イノベーションと言ったりします)」を、カルマンゲインという重みで足し合わせる形をしています。
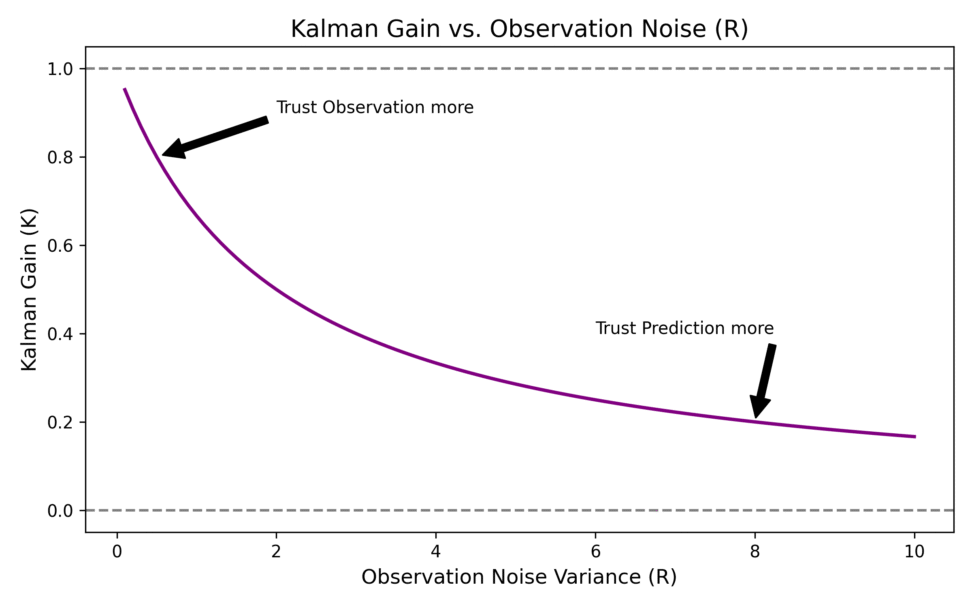
カルマンゲイン $K_t$ は、「予測の不確実性」と「観測の不確実性」の比率によって決まります。観測ノイズ $R$ が非常に大きい場合、カルマンゲインは小さくなり、フィルタは観測値をあまり信用せずに予測値を重視します。逆に、観測が非常に正確であれば、カルマンゲインは大きくなり、観測値に基づいて大胆に予測を修正します。
カルマンゲインについて
カルマンゲインは、観測に基づく状態推定値の更新にどれだけの重みを置くかを決定します。観測の不確かさが大きい場合、ゲインは小さくなり、新しい観測による影響が小さくなります。
一方で、予測の不確かさが大きい場合、ゲインは大きくなり、新しい観測による影響が大きくなります。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!






