12/26/2024 / 最終更新日時 : 01/07/2025 bluest Python

【完全版】MMMを課題設定から考える｜Google Meridian

Media Mix Model｜MMM

MMM は、過去の広告支出や売上データを用いて、各マーケティング施策が売上（KPI）にどの程度貢献したかを定量的に分析する手法です。これにより、予算配分の最適化や将来のマーケティング戦略の策定に役立てることができます。

マーケティングミックスモデルと呼ばれたりしますね。

Googleだと、Media Mix Modelと呼んでいるようです。

意外と古くから考えられていた手法ではあり、説明変数にマーケチャネルのコストデータ等をインプットにして、目的変数（予約や売上などのKPI）を求める回帰モデルを作ります。

MMMの目的

効果測定: 各マーケティングチャネルの ROI（投資対効果）を評価
予算配分: 限られた予算を最適なチャネルに配分
将来予測: さまざまなシナリオにおける売上予測

結構多いのが、各マーケチャネルの貢献度の可視化です。

なので、目的変数の予測精度というよりも回帰係数の推定精度が注目される場合が多いです。

効果測定であれば、予実管理に使えますね。また集客費用の最適化をするには、各マーケティングチャネルの集客効率を見て、投資判断をする必要があります。

一方、プライバシーの観点でも今後重要性を増すと考えられています。

MMMの入力は、通常集計されたメディアコストと収益データであり、クリック、ビュー、または個々の売上コンバージョンは使用しません。

３rd party Cookieの規制など、事業会社が取れる個人情報が少なくなってきており、それによりアトリビューションによる貢献度の推定もやりづらくなっていくと考えられています。

より統計的な手法でメディアの価値を紐解く必要が出てきそうという背景もあり、近年注目を浴びています。

【重要】MMMで解きたい課題ってなに？？

そもそもこの課題背景が抜けて流行っているからMMMを使いたい、となっているパターンも多いと思います。

事業側からデータを受領して、
ベンダーに作ってもらい、
ダッシュボードまで構築してもらって
一定の頻度でレポートをもらう

という契約となると、ランニングコスト含め年間1000万円を超えたりするので、ちゃんとMMMでときたい課題を明確にして、「外注か内製か？」などメリデメを整理して保守運用まで考え抜きましょう。

これ結構危険だとは思っていて、「何に使うのか？」「本当にMMMが最適な解なのか」を精査せずに検討が進むと、「作ってもらって終わりになる」パターンが合ったりします。

ちょっとバンダイナムコにいい事例があったので、事例を踏まえてMMMの概要を見てみましょう！

プロジェクトの背景

広告投資: バンダイナムコグループは2022年度に約570億円を広告宣伝に投資。この投資効果を最大化するため、広告予算の最適配分が重要な課題となっている。
目的: 特定のスマホゲームタイトルにおける広告宣伝費の配分を最適化し、新規インストール数を最大化すること。

さすが大企業、広告宣伝費がとんでもないですね。

広告予算配分の課題

効果の把握: 複数の広告施策が同時に行われ、各施策の効果を正確に測定することが難しい。
アドストック問題: 広告施策の効果が即座に現れず、時間差で影響が出ることがある。
収穫逓減問題: 効果の高い広告媒体に予算を集中させても、一定のコストを超えると効果が減少する。

さて、商材の種類にもよるのですが、基本的にテレビCMやWEBプロモ系の認知系施策は施策の効果が定量的に見えづらいです。なので、投下量が適正化できていない場合も多いです。

一方で、リスティング広告等のAdobe等のタグを埋め込んでコンバージョンを計測するチャネルになると、ある程度効果は可視化でき、CPAカーブもある程度精緻に引くことができます。

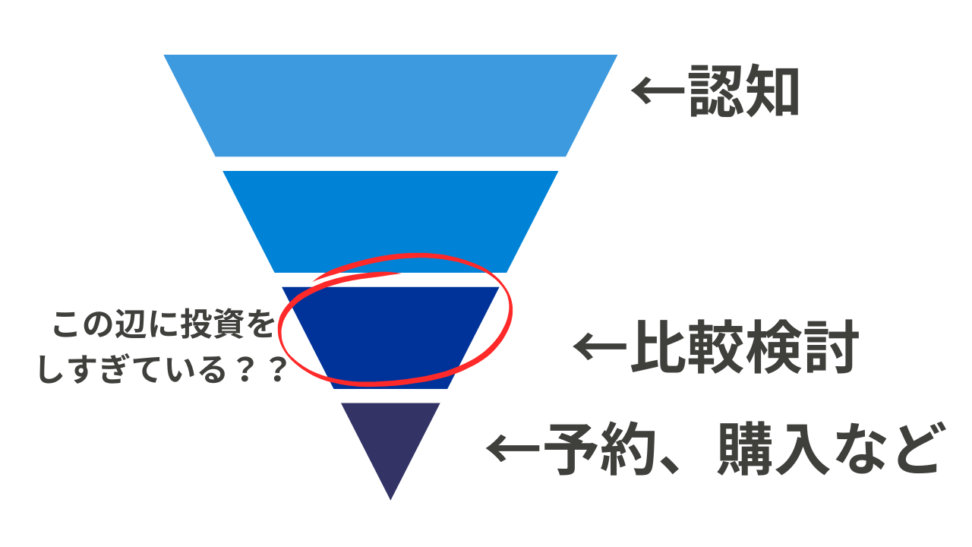
ただ、上記を前提にすると、リスティング広告等の効果を計測しやすいチャネル、つまりラストタッチに比重が置かれた投資配分になっていないか、というのが仮説の始まりです。

ときたい問い

本来認知系の施策にも投資をしたいが、効果計測が精緻にできていないために、マーケティングファネルの下の部分の投資に重きが置かれすぎてはいないか？

このために、全チャネルの投資コストのデータ等を使い、認知系施策含めてKPIへの貢献度を可視化したいということですね。

モデル概要

ここで作るMMMはこのようなモデルです。

定義

過去の広告データを基に、インストール数や売上などのKPIと各種マーケティング施策の関係を分析し、最適化シミュレーションを行う手法。

バンダイナムコでは、乗法モデルを採用し、各変数の寄与度を精緻に見積もったようですね。

具体的な工夫

アドストックと収穫逓減の対応: モデルを2段階で作成し、広告の効果を時間的に考慮。
フラグデータの連続値化: イベントの効果が時間とともに減衰することを考慮し、データを連続的に表現。
トレンド成分の抽出: オーガニックなインストール数のトレンドをストア内検索数から推定。

この例をもとに、MMMのモデル構造について学んでいきましょう。

例えばこんな感じでしょうか。

$${\begin{equation}
Y_t = Trend_t \times \prod_{i=1}^{n} (AdStock_i(X_{i,t}))^{\beta_i} \times \epsilon_t
\end{equation}}$$

${Y_t}$ : 時点 ( t ) における売上（またはインストール数）
${Trend_t}$ : 時点 ( t ) におけるトレンド成分（ストア内検索数などから推定）
${X_{i,t}}$ : チャネル ( i ) の時点 ( t ) における広告支出
${\beta_i }$: チャネル ( i ) の効果を表す係数
${ \epsilon_t }$: 誤差項

アドストック変換

アドストック変換は、広告の遅延効果を考慮するために用いられます。

これも商材やクリエイティブの内容にもよりますが、広告の効果が即日効くとは限りません。例えば、ブランドイメージの向上を狙ったTV CMだと、効果がじわじわと遅れて現れることはイメージしやすいのではないでしょうか。

$${AdStock_i(X_{i,t}) = \sum_{l=0}^{L} \lambda_i^l X_{i,t-l}}$$

${\lambda_i}$ : チャネル ( i ) の減衰率（ ${0 < \lambda_i < 1}$ ）
L : 最大ラグ期間

収穫逓減（飽和効果）

収穫逓減は、広告支出の増加に伴う効果の逓減を表現するために、べき乗変換を適用します。上記の基本モデル式ですでに組み込まれています。必要に応じてHill functionなどを利用することもあります。

この収穫逓減（いわゆる効果がサチッていく話）と広告効果のラグを如何に実態に沿わせるかで、MMMの出来は変わります。

トレンド成分

トレンド成分 ( ${Trend_t}$ ) は、ストア内検索数など、広告以外の要因による売上変動を表します。

要は市況ですね。

例えば、以下のように線形トレンドで近似できます。

\begin{equation}
Trend_t = \alpha + \gamma t
\end{equation}

${\alpha}$ : 定数項
${\gamma }$: トレンドの傾き

より複雑なトレンドを表現するために、より高次の多項式や他の関数を用いることもあります。

モデルの推定と評価

このモデルは、MCMC（Markov Chain Monte Carlo）アルゴリズムを用いて推定されます。

各パラメータの事後分布が得られ、不確実性を考慮した分析が可能になります。

MCMCの詳細については、こちらをご覧ください。

モデルの精度は、MAPE（平均絶対パーセント誤差）を用いて評価されます。

バンダイナムコの事例では、MAPE 7.0%を達成しているようですね。

\begin{equation}
MAPE = \frac{1}{n} \sum_{t=1}^{n} \left| \frac{Y_t – \hat{Y}_t}{Y_t} \right| \times 100
\end{equation}

学習に使わなかったデータを使って、testMAPEを確認するのがセオリーなのですが、この指標だけだと各説明変数の貢献度が正しいかどうかはわからないです。

これはMMMを導入したい事業側の課題背景にもよりますが、以下のように定性的な評価観点も確認した方が良いと思います。

評価
ポイント

・各マーケティングチャネルの論理構造がモデルにしっかりインプットされているか

・予測の精度はもちろん、各チャネルの貢献度が事業側の肌感と合っているかどうか

特に二つ目は非常に大事です。

ーここからフィクションー

外注したモデルによっては、特定のチャネルや施策に貢献度が寄るようなパラメータ調整がなされているかもしれません。

例えば、テレビCMの枠を扱う広告代理店によるMMM開発の場合、MMMのアウトプットを通して大企業の集客費用についての意思決定をある程度コントロールできるのであれば、あえてテレビCMの投資効率が良いと見せ、自社への出稿金額を上げてもらうというやり方もあり得るかもしれませんね。

ーー

なので、普段リスティング広告の運用をしている担当など、ある程度投下量に対する増分コンバージョン（CV）が把握できている事業側とアウトプットを確認しつつ開発を進めていくのが、結果的に「使えるMMM」につながると思います。

逆に、肌感だけでMMMのパラメータを事業側が調整しすぎるのは、推定結果に恣意性が介在するので、おすすめはしません。

結果

バンダイナムコでは、過去の実績に基づく最適化により、インストール数を1.5倍に引き上げる可能性が示されている

すごい結果ですね。

MMM｜Google Meridian

さて、事例の理解ができたと思うので、GoogleのMMMモデルの紹介をします。

25年からGoogleからMeridianという最新MMMフレームワークがオープンソースとして一般リリースされるようです。オープンソースなので、広告主はMeridianを使用して、独自のインハウスモデルを構築することができます。

入力データとしては50以上のエリアと2〜3年間の週次データで階層ベイズによるアプローチのようです。

Meridianを使う目的

上でも解説しましたが、Meridianも以下の問いに対する答えを提供することを目的としています。

さまざまなマーケティングチャネルが、収益やその他の主要業績評価指標（KPI）にどのように影響したか？
マーケティング投資収益率（ROI）はどの程度であったか？
将来的にマーケティング予算をどのように配分すればよいか？

モデルの概要

\begin{align*}
y_{g,t} = \mu_t + \tau_g &+ \sum\limits_{i=1}^{N_{C}}
\gamma^{[C]}_{g,i} z_{g,t\,i} \\
&+ \sum\limits_{i=1}^{N_N} \gamma^{[N]}_{g,i} x^{[N]}_{g,t,i} \\
&+ \sum\limits_{i=1}^{N_M} \beta^{[M]}_{g,i} HillAdstock \left(
\left\{ x^{[M]}_{g,t-s,i} \right\}^L_{s=0}\ ;\
\alpha^{[M]}_i, ec^{[M]}_i, \
slope^{[M]}_i \right) \\
&+ \sum\limits_{i=1}^{N_{OM}} \beta^{[OM]}_{g,i} HillAdstock \left(
\left\{ x^{[OM]}_{g,t-s,i} \right\}^L_{s=0}\ ;\
\alpha^{[OM]}_i, ec^{[OM]}_{i}, \
slope^{[OM]}_{i} \right) \\
&+ \sum\limits_{i=1}^{N_{RF}} \beta^{[RF]}_{g,i} Adstock \left(
\left\{ r^{[RF]}_{g,t-s,i} \cdot Hill \left(
f^{[RF]}_{g,t-s,i};\ ec^{[RF]}_{i},\ slope^{[RF]}_{i}
\right) \right\}^L_{s=0}\ ;\ \alpha^{[RF]}_{i} \right) \\
&+ \sum\limits_{i=1}^{N_{ORF}} \beta^{[ORF]}_{g,i} Adstock \left(
\left\{ r^{[ORF]}_{g,t-s,i} \cdot Hill \left(
f^{[ORF]}_{g,t-s,i};\ ec^{[ORF]}_{i},\ slope^{[ORF]}_{i}
\right) \right\}^L_{s=0}\ ;\ \alpha^{[ORF]}_{i} \right) \\
&+ \epsilon_{g,t}
\end{align*}

最初に見ると「うっ」てなりますね。

${\mu_t}$：時間変動定数項（トレンドと季節性を考慮）knotsを用いて柔軟にモデル化される（後述）。
${τ_g}$：地域 g の定数項（固定効果ですね）

などのベースラインは理解できますが、メディア変換関数が後ろにたくさんくっついていてわかりづらいです。

一つずつ見ていきましょう。

階層構造

まずは、モデルの全体構造から抑えた方が良いです。

Meridianは、エリアレベルと全国レベルのパラメータを階層的に関連付けています。

具体的には、エリアレベルの係数 ${β_{g,m}}$ と ${γ_{g,c}}$ は、全国レベルの係数 ${\beta_m}$ と ${\gamma_c}$ を中心とする正規分布に従うと仮定します。

$${
\beta_{g,m} \sim \mathcal{N}(\beta_m, \sigma_{\beta,m}^2)
}$$

$${
\gamma_{g,c} \sim \mathcal{N}(\gamma_c, \sigma_{\gamma,c}^2)
}$$

階層構造により、エリアごとのマーケティング効果の差異を捉えつつ、全体的な傾向を把握することができます。

例えば、ある地域ではテレビ広告の効果が高いが、別の地域ではオンライン広告の効果が高いといった場合には、エリア粒度まで分解した時点×エリアのパネルデータが分析には必要ですよね。

階層ベイズからおさらいしたい人は、こちらがおすすめです。

コントロール変数と非メディア処理変数

コントロール変数

$${\sum_{i=1}^{N_C}\gamma_{g,i}z_{g,t,i}}$$

コントロール変数の影響を表す項。

価格やプロモーションなど、マーケティング活動以外の要因を考慮します。

非メディア処理変数

$${\sum_{i=1}^{N_N}γ_{g,i}x_{g,t,i}}$$

非メディア処理変数の影響を表す項。

マーケティング活動以外の要因のうち、特に注目する変数を考慮します。

$x_{g,t,i}$: 各メディアチャネルへの支出やインプレッション数など
${z_{g,t,i}}$ : i 番目のコントロール変数（価格、プロモーションなど）
${\gamma_{g,i}}$：係数

メディア変換関数

各項は、アドストック関数やhill関数を使って、広告特有の投下量とKPIの連動を捉えられた形で表されます。

メディアのhillアドストック

$${\sum_{i=1}^{N_M}β_{g,i}HillAdstock(…)}$$

各メディアチャネルへの支出やインプレッション数などを考慮します。

オーガニックメディアのhillアドストック

$${\sum_{i=1}^{N_{OM}}β_{g,i}HillAdstock(…):}$$

オーガニックメディア変数の影響を表す項。オーガニック検索など、費用をかけずに獲得したメディアへの露出を考慮します。

SNS投稿なども変数に入れられそうですね。

メディアと同じく、HillAdstock関数を用いて、飽和効果と遅延効果を考慮します。

リーチ＆フリークエンシーのアドストック

$${\sum_{i=1}^{N_{RF}}β_{g,i}Adstock(…)}$$

広告のリーチ（到達人数）とフリークエンシー（一人あたりの広告表示回数）を考慮します。

さらっと書きましたが、これまでのMMMだとインプレッションを総量でインプットすることがセオリーだったと思います。送料をリーチ数と頻度に分解できるのは、一歩詳細なデータをみえているというわけですね。嬉しい。

オーガニックリーチ＆フリークエンシーのアドストック

$${\sum_{i=1}^{N_{ORF}}β_{g,i}Adstock(…)}$$

オーガニックリーチ＆フリークエンシー変数の影響を表す項。

さて、説明を端折っていたアドストック関数とhill関数について深掘ります。

アドストック関数とヒル関数

Adstock関数

Adstock関数は、過去の広告効果が現在のKPIにも影響を与えることを考慮するための関数です。

広告の効果は、即座に現れるとは限らず、時間をかけて徐々に浸透していくことがあります。

このような遅延効果をモデル化するために用いられます。

$${ a_{g,t,m} = x_{g,t,m} + \lambda_m a_{g,t-1,m} }$$

${a_{g,t,m}}$: 地域 ${g}$、時点 ${t}$、メディアチャネル ${m}$ におけるAdstock
${x_{g,t,m}}$: 地域 ${g}$、時点${t}$、メディアチャネル ${m}$ におけるメディア変数の値（例：広告支出）
${λ_m}$: メディアチャネル ${m}$ のAdstock rate（減衰率）

ちなみに、Adstock rate (λm) は、過去の広告効果が現在のKPIにどの程度影響するかを表すパラメータです。

ポイント

Adstock rateが大きいほど、過去の広告効果の影響が大きくなります。

Hill関数

Hill関数は、メディア支出の増加に伴い、その効果が逓減していくことを考慮するための関数です。ある程度の支出までは効果が大きく増加しますが、支出を増やし続けても、効果の増加は徐々に小さくなっていきます。

このような飽和効果をモデル化するために用いられます。

$${
hill_{g,t,m} = \frac{x_{g,t,m}^{\theta_{m,1}}}{k_m^{\theta_{m,1}} + x_{g,t,m}^{\theta_{m,1}}}
}$$

${hill_{g,t,m}}$: 地域 ${g}$、時点 ${t}$、メディアチャネル ${m}$ におけるHill関数の値
${x_g,t,m}$: 地域 ${g}$、時点 ${t}$、メディアチャネル ${m}$ におけるメディア変数の値（例：広告支出）
${k_m}$: メディアチャネル ${m}$ のHill関数のEC50（半値濃度）
${θ_{m,1}}$: メディアチャネル ${m}$ のHill関数のslope（傾き）

${EC50 :(k_m)}$ は、効果が最大値の半分になるメディア支出を表すパラメータです。

${slope :(θ_{m,1})}$)は、飽和効果の強さを表すパラメータです。

ポイント

slopeが大きいほど、飽和効果が強く、支出を増やしても効果の増加は小さくなります。

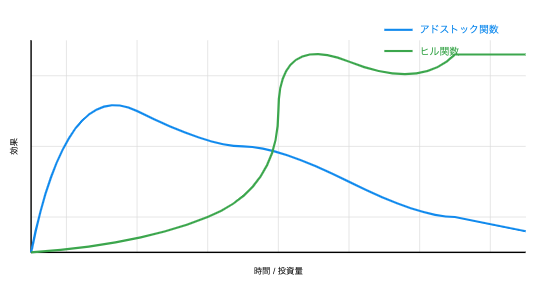
最後に形を確認しましょう。

X軸は時間もしくは投資量を表し、 Y軸は効果（レスポンス）を表しています。

ヒル関数は、S字カーブを描いていますね。
投資量が少ない時は効果が緩やかで、ある閾値を超えると急激に効果が上がる様子を表しています。
その後、飽和して効果の増加が緩やかになるというのが特徴です。

一方、アドストック関数は初期の効果が高く、時間とともに徐々に減衰していく広告投資の継続的な効果を示していますね。

Knotsとは

モデルの定数項である${\mu_t}$について深掘りします。

ここでは、時間変動定数項をモデル化するために、knotsと呼ばれる概念を用います。

Knotsは、時間軸上の特定の時点を指し、MeridianではこれらのknotsにおけるKPIの値をパラメータとして推定します。各時点におけるKPIの値は、隣接するknotsの値を重み付け平均することで算出されます。

この重みは、各時点とknotsとの間のL1距離に基づいて決定されます。

メリット

Knotsの数を増やすと、モデルはより複雑になり、データへの適合度が高まる

あるあるですが、knotsの数を増やしすぎると、過学習が発生し、モデルの汎化性能が低下するというデメリットもあります。

過学習が発生したり、メディア効果の推定値が非現実的になった場合は、knotsの数を減らすのが良さそうですね。

数式で理解する｜Knotsと時間変動インターセプト

Meridianの時間変動インターセプト (${\mu_t}$) は、knotsの値 (${b_1,b_2,…,b_K}$) と重み行列 (${W}$) を用いて、以下のように表されます。

$${\mu=W∗b}$$

${\mu}$: 各時点 ${t=1,…,T}$ における時間変動インターセプトを表す ${1×T}$ のベクトル
${W}$: 各時点とknotsとの間のL1距離に基づいて算出される ${T×K}$ の重み行列
${b}$: knotsにおけるKPIの値を表す ${K×1}$ のベクトル

例えば、3年間の週次データ（${T=52×3=156}$）を分析する場合、knotsを${12}$個（${K=12}$）設定すると、各knotは13週間（約3ヶ月）ごとに配置されます。各時点における時間変動インターセプトは、その時点に最も近い2つのknotsの値を、L1距離に基づいて重み付け平均することで算出されます。

コードベースでいうとKnotsの設定は、knots引数で行うようで、 Knotsの位置をリストで指定することも、knotsの数を指定することもできます。Knotsの数を指定した場合、knotsは等間隔に配置され、両端点はt=1とt=Tに固定されます。