【高校数学でわかる】分散と標準偏差をわかりやすく解説|散らばりの指標
分散(variance)と標準偏差(standard deviation)
こんにちは、青の統計学です。
今回は、統計の基本である分散と標準偏差について解説していきます。
高校数学でも扱われる内容なので、高度な数学は必要ございません。
例として毎日サッカー部の出席者を計測していきます

40日連続で部活に来ている人を数えていきましょう。
26,21,23,14,21,25,21,19,20,24,18,23,23,24,21,18,21,21,24,26,24,23,23,21,19,20,25,26,25,26,21,19,20,20,21,27,26,21,29,19こんな感じなりました。
多い日は30人近く部員が集まり試合ができそうですが、少ない日は14人とフットサルがギリギリです。
(1)最大値、最小値、第1四分位数、中央値、第3四分位数をそれぞれ求めてみましょう。(大変ですので平均は結構です)
答え(1)左から、最小値、第1四分位数、中央値、第3四分位数、最大値です。
Min. 1st Qu. Median Mean 3rd Qu. Max.
14.00 20.00 21.00 22.20 24.25 29.00 四分位数や中央値は小さい順に並べるとわかりますね。
一つに絞れないならば、2つの平均をとってあげてください。
18 18 19 19 19 19 20 20 20 20 21 21 21 21 21 21 21 21 21 21 23 23 23 23 23 24 24 24 24 25 25 25 26 26 26 26 26 27 29ヒストグラムは以下のようになります。
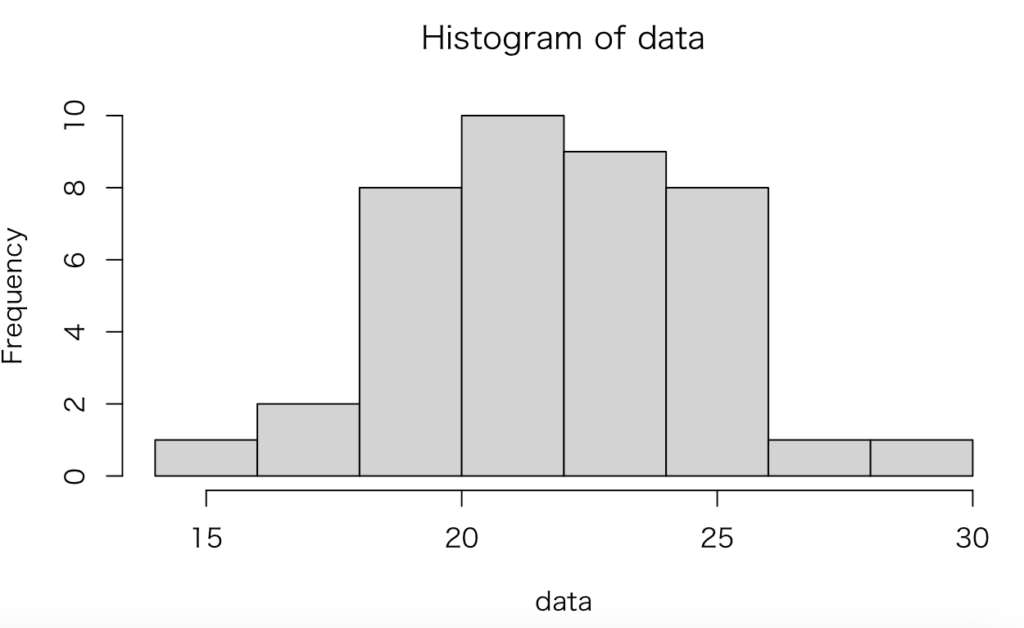
大体20から25人がボリュームゾーンらしいです。
では、どのくらい出席部員数にばらつきがあるのでしょうか?
分散(variance)
大きく分けてデータの指標は、散らばりの指標と位置の指標の2種類があります。
標本平均や最頻値、中央値などは位置の指標といわれる一方、分散と標準偏差は散らばりの指標と呼ばれます。
分散とは、あるデータのばらつきを表す指標です。
求め方は2通りあります。
$$V(X)=\frac{1}{N}\sum_{i=1}^{N}(x_{i}-\overline{x})^2$$
まず、各データ(14人や25人、、、)から平均22.20を引きます。
残った値を「偏差」と呼びます。
これを全てのデータに対して行い、平均を取ります。
$$V(X)=\frac{1}{N}\sum_{i=1}^{N}x_{i}^2-\overline{x}^2$$
一方こちらは、各データを2乗していって平均を取ります。その値から、データの平均の2乗を引きます。
どちらの求め方がいいかは、問題によります。
ちなみに、この部員出席数の分散は9.189744でした。
補論|不偏分散について
少し発展的な内容を加えます。
統計学には、不偏性という「期待値が母集団の統計量と等しい」という概念があります。
我々が真に知りたいのは、母集団の性質であり、サンプルデータの性質ではありませんので、統計量がこの性質を持つことは望ましいです。
$$E[\overline{X}]=\mu$$
先ほどまで求めていた分散が、母集団からサンプルをとり、標本から分散を求めていた場合はどうでしょうか?
そもそも、観測データの平均値を使って分散を求めているので、母集団の散らばりとは異なりますよね。
つまり、標本データは母集団よりもnが小さいため構造上真の分散(母分散)を過小に評価してしまいます。
このため、サンプル数nを使わず自由度n-1を使って分散を求めます。
この時求められる分散を不偏分散と呼んでいます。
$$\frac{1}{N-1}\sum_{i=1}^{N}x_{i}^2-\overline{x}^2$$
詳しくは以下のコンテンツをご覧ください。
標準偏差(standard deviation)とは
$$\sigma=\sqrt{V(X)}$$
分散の平方根です。
ちなみに、この部員出席数の標準偏差は3.031459でした。
標準偏差はデータのばらつきや分散を定量的に表現する重要な統計指標です。
標準偏差は、データセットの各値が平均からどれだけ離れているかを示し、データの分布の形状に関する情報を提供してくれます。
分散とは違い、スケールを戻せるところが嬉しいですね。
標準偏差の使い方
データの分布を分析する:標準偏差を使用して、データセットの正規分布の特徴を把握し、異常値や外れ値を検出することができます。
この用途に関しては、歪度や尖度も使えます。
この辺りは、モーメントなどの知識が必要です。
モデルの性能評価: 標準偏差は予測モデルの性能を評価する際にも利用されます。
例えば、回帰モデルの残差(実際の値と予測値の差)の標準偏差を計算することで、モデルの精度や信頼性を評価できます
では、実際に分散や共分散について問題を解きたい方は以下の記事をご確認ください。
補足|変動係数(Coefficient Valuation)について
やや発展的な内容ですが、統計検定2級で登場する変動係数について解説いたします。
変動係数は、データセットの標準偏差を期待値で割った値です。
$$CV=\frac{\sqrt{V[X]}}{E[X]}$$
変動係数は相対的なデータのばらつきを示す指標であり、異なる単位やスケールのデータセットを比較する際に特に有用です。
変動係数が大きいほど、データのばらつきが大きいことを示します。
逆に、変動係数が小さいほど、データのばらつきが小さいことを示します。
import numpy as np
import pandas as pd
# 2つのデータセットを定義します
dataset1 = np.array([150, 155, 154, 160, 162])
dataset2 = np.array([40, 42, 51, 55, 50])
# 変動係数を計算する関数を定義します
def coefficient_of_variation(data):
mean = np.mean(data)
std_dev = np.std(data)
return (std_dev / mean) * 100
# 各データセットの変動係数を計算します
cv_dataset1 = coefficient_of_variation(dataset1)
cv_dataset2 = coefficient_of_variation(dataset2)
# 変動係数を表示します
print(f"Dataset 1 Coefficient of Variation: {cv_dataset1:.2f}%")
print(f"Dataset 2 Coefficient of Variation: {cv_dataset2:.2f}%")
# 変動係数を比較し、ばらつきが大きいデータセットを判断します
if cv_dataset1 > cv_dataset2:
print("Dataset 1 has a larger coefficient of variation.")
elif cv_dataset1 < cv_dataset2:
print("Dataset 2 has a larger coefficient of variation.")
else:
print("Both datasets have the same coefficient of variation.")
pythonで、二つのデータセットの変動係数を比較するプログラムを書きました。
データセット1は身長をデータセット2は体重を意識して適当に作りました。
変動係数が大きいデータセットを上げてくれます。試してみてください。
このように、データセット間でどの程度ばらつきがあるのか、単位がcmやkgなどになっていると適切に評価が行えないです。
こうした場合に変動係数を使い、期待値でスケーリングしているということです。
同じような概念として標準化や中心化があります。
より機械学習の分野を深ぼっていくと、スケーリングはモデルの学習精度の差にも関わっていきます。
逆にノードにおける特徴ベクトルの大小比較となる決定木系のアルゴリズムはスケーリングの旨みが少ないなど、奥が深いです。
気になる方は以下のコンテンツをご覧ください。
脱線してしまいましたが、分散と標準偏差について理解が深まったかと思います。
データの特徴を表す基本的かつ最も重要な指標です。


