【生存時間解析】ワイブル分布をわかりやすく｜確率分布とパラメータ推定方法

ワイブル分布は、製品の故障時間や材料の寿命、医療分野の生存時間解析などで広く使われている連続確率分布です。機械部品の寿命データや、生体における生存時間データを扱う際に非常に有用で、信頼性工学や生存分析の分野で欠かせない存在となっています。

また、形状パラメータを調整することで指数分布やレイリー分布などを近似できるため、柔軟性の高さが特徴です。

1. ワイブル分布の概要

1-1. ワイブル分布は「最弱リンクモデル」から誕生

ワイブル分布の背景には、「全体の強度や寿命は最も弱い箇所によって決定される」という最弱リンクモデルの考え方があります。鎖であれば最も弱い輪が切れた時点で鎖全体が破断し、製品であれば最も早く故障した部品が全体の寿命を左右するといったイメージです。

形状パラメータ ${k}$（または ${m}$）とスケールパラメータ ${\lambda}$（または ${\eta}$）の2つのパラメータを用いることで、初期不良が多い現象（${k < 1}$）から、時間が経つほど故障率が上がる摩耗故障現象（${k > 1}$）まで、さまざまなパターンを表現できます。

1-2. ワイブル分布の確率密度関数と分布関数

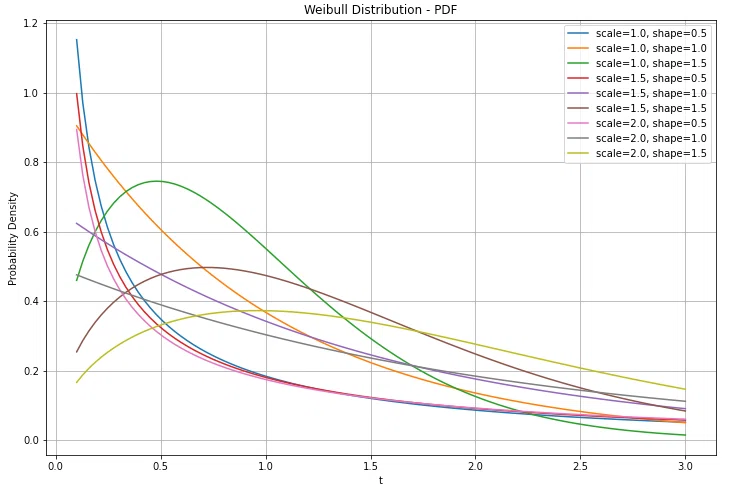
ワイブル分布の確率密度関数（PDF）は、以下のとおりです（${x \geq 0}$）

$${f(x; k, \lambda) \;=\; \frac{k}{\lambda} \Bigl(\frac{x}{\lambda}\Bigr)^{\,k-1} \exp\Bigl[-\bigl(\tfrac{x}{\lambda}\bigr)^{k}\Bigr]}$$

${k > 0}$ は形状パラメータ（shape parameter）
${\lambda > 0}$ はスケールパラメータ（scale parameter）

一方、累積分布関数（CDF）は、

$${F(x) \;=\; 1 \;-\; \exp\Bigl[-\bigl(\tfrac{x}{\lambda}\bigr)^{k}\Bigr]}$$

となります。

この ${F(x)}$は「ある時点 ${x}$ までに故障（もしくは事象が発生）している確率」を意味します。

2. 形状パラメータとスケールパラメータの意味

2-1. 形状パラメータ ${k}$

${k < 1}$：分布が左に裾を引き、初期不良が目立つ傾向を示唆
${k = 1}$：指数分布と同じ形状になり、故障率が一定（経時劣化や初期不良があまり影響しない）
${k > 1}$：分布が右に裾を引き、時間の経過とともに故障率が増加する“摩耗故障型”

つまり、製品やシステムがどのような故障パターンを持つかを大まかに推察できるのが形状パラメータです。

2-2. スケールパラメータ ${\lambda}$

スケールパラメータ ${\lambda}$ は、分布の広がりを決定づける指標です。値が大きいほど寿命や故障時間が長めの領域に分布が広がることを意味します。

寿命データ解析で用いられる場合、${\lambda}$ は「製品や生物個体における特性寿命」とも呼ばれ、約63.2%の個体・部品がそれまでに故障するとも解釈されます。

これは

$${F(\lambda) = 1 – e^{-1} \approx 0.632}$$

となることに対応します。

上記のようなパラメータを操作しながらワイブル分布の動きを見る場合、青の統計学-DS Playground-の確率分布可視化ツールが便利です。

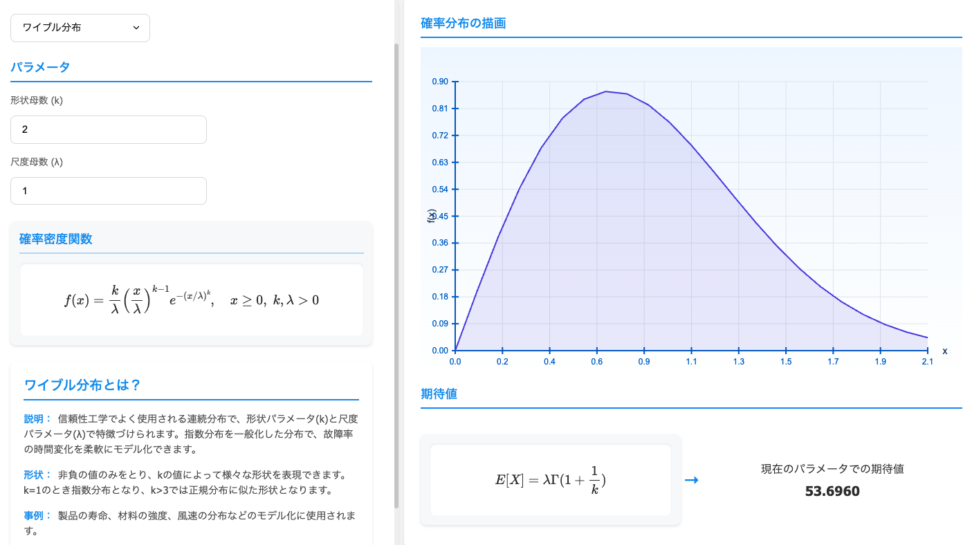
以下のリンクをクリックすると、ワイブル分布の描画ページに飛びます。

確率分布可視化ツール｜ワイブル分布

3. 危険率（ハザード関数）と生存関数

ワイブル分布は、生存時間解析の文脈でもよく登場します。生存関数 ${S(t)}$ は「まだ故障していない（生存している）確率」であり、累積分布関数との関係は

$${S(t) = 1 – F(t) = \exp\Bigl[-\Bigl(\tfrac{t}{\lambda}\Bigr)^{k}\Bigr]}$$

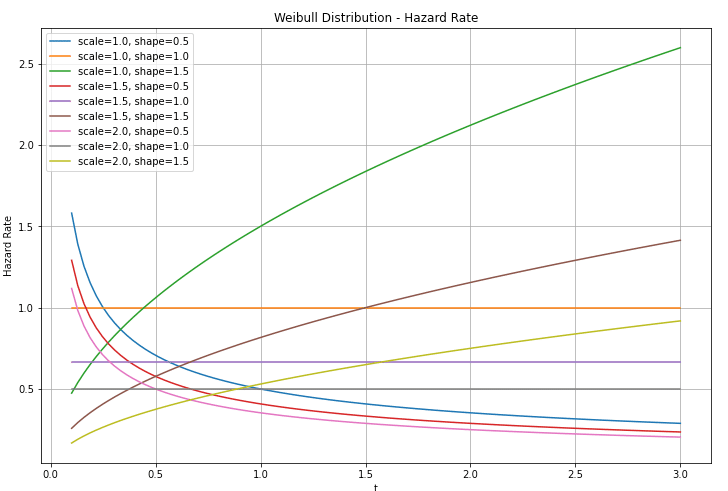
一方、危険率（ハザード関数）${h(t)}$ は、

$${h(t) = \frac{f(t)}{S(t)} = \frac{\tfrac{k}{\lambda}\,\Bigl(\tfrac{t}{\lambda}\Bigr)^{k-1} \exp\Bigl[-\bigl(\tfrac{t}{\lambda}\bigr)^k\Bigr]} {\exp\Bigl[-\bigl(\tfrac{t}{\lambda}\bigr)^k\Bigr]} = \frac{k}{\lambda}\,\Bigl(\tfrac{t}{\lambda}\Bigr)^{k-1}}$$

${k}$の値によって、危険率が時間とともに上昇・下降・一定になる様子を把握できるわけです。

4. ワイブル分布の指数分布との関係

前述のように、形状パラメータ ${k = 1}$ のとき、ワイブル分布は指数分布に一致します。指数分布は故障率（ハザード）が一定であるという特性を持つため、もし実際のデータが時間の経過に左右されない「偶発故障型」だと推定されるなら、ワイブル分布の特別なケースとして指数分布を使うことができます。

しかし、多くの機器・製品は経年劣化などを起こすため、常に故障率が一定とは限らないのが現実です。

その点、形状パラメータを自由に設定できるワイブル分布は、幅広い故障パターンを表現しやすい分布として重宝されています。

5. ワイブル分布のパラメータ推定方法

実際にワイブル分布を適用したい場合、観測データ（故障時間や寿命時間） から kkk と λ\lambdaλ を推定します。代表的な方法は以下のとおりです。

最尤推定法（MLE）
尤度関数を最大化するパラメータを探索する方法。
- ${ \ell(k, \lambda) = \sum_{i=1}^n \ln f(x_i; k, \lambda)}$数値計算的に解くのが一般的です。
確率紙プロットによる推定
ワイブル分布専用の確率紙（Weibull probability paper）にデータをプロットし、近似的に直線を引くことでパラメータを読取る手法。直感的に分布への当てはまりを視覚的に確認できます。
モーメント法
標本平均や標本分散などのモーメントを用いて、理論モーメントと一致させる方法。ただし、寿命データの場合は最尤推定や確率紙法の方がよく用いられます。