統計検定3級|合格率や出題範囲、勉強法を徹底解説【2025年最新版】
統計検定3級とは?
統計検定3級は、統計学の基礎知識を評価するために設けられた重要な資格試験で、データを適切に扱う能力や、統計学の基本的な概念を理解していることを証明することを目的としています。
1級からさまざまなレベルがある中で、3級は入門的な位置づけにあり、統計学を学び始めたばかりの学生や、業務で統計データを扱う社会人に最適です。

数学を高校以来やっていない、統計や確率の考えに触れたことがない。という方には、2級ではなく3級から始めることをお勧めします。
統計学に対する理解を深め、実務に活かすための第一歩として位置づけられていますね。
試験の概要
統計検定3級は、統計学の基礎的な知識を評価するための試験で、一般財団法人統計質保証推進協会が実施しています。この試験は、大学基礎レベルの統計学の知識を必要とし、統計活用力を認定する資格です。
試験形式: コンピュータベースのテスト(CBT方式)で、問題数は約30問です。出題形式は選択肢からの選択で、解答はマウスやキーボードを使用して行います。

実は準1級までは通年で受けられるので、自分のペースで勉強しやすい+リベンジしやすいので、統計検定はお勧めです!
試験時間: 試験は60分間で行われます。
出題範囲: 主に以下の内容が含まれます。
- データの種類
- 基本的な確率分布(例: 二項分布)
- 平均、中央値、分散、標準偏差などの計算
- グラフ表現やデータの可視化に関する問題。
記事の後半で、出題範囲について軽く扱いますので、最後まで見てやってください:)
合格基準: 合格率はおおよそ65%から75%の間で、比較的高い合格率を誇ります。しっかりとした対策を行うことで合格を目指すことが可能です。
持ち込み可能な道具: 計算機の持ち込みが許可されており、普通電卓や事務用電卓を使用できますが、特定の計算機(プログラム可能なものなど)は持ち込み不可です
統計検定3級のメリット
統計検定3級は、統計に関する基礎的な知識を身につけるための第一歩です。
受ける上でのいくつかのメリットを挙げてみます。
学習リソースが豊富
最近はデータサイエンスや生成AIの盛り上がりもあり、IT業界へ注目が集まっていますね。とはいえ、データや数字を適切に扱えるor語れる人材はそういません。なので、統計検定自体の注目も上がっており、年々受験者は増えています。

自己学習がしやすい環境が整っていますね。
近年では、統計学を学ぶためのオンラインプラットフォームも増えており、柔軟に学習できる環境が整っています。例えば、青の統計学では、統計の基礎を学ぶための多様な教材が提供しています。
統計検定等、データサイエンスの最新情報にアクセスしたい方は 以下のコンテンツがお勧めです!
統計的思考の育成
個人的にはこれが、何より大事なメリットと思っています。データや数字、グラフに騙されない&誤解して伝わらないような資料の語り方ができるようになってきます。所謂データリテラシーの向上ですね。
ビジネスの現場だと、データを正しく解釈し活用する能力が求められています。統計検定3級を通じて、データリテラシーが向上し、情報の信憑性を見極める力が養われます。
統計検定3級の取得は、個人としてのスキルアップだけでなく、キャリアの選択肢を広げるためにも非常に有益です。これから統計を学ぶ方は、ぜひ挑戦してみてください。
知識の強化
- 基礎からの理解:統計検定3級では、データの収集や分析方法、確率の基礎など、統計学の根本的な概念を学びます。これにより、統計に対する理解が深まり、実務に役立てることができます。
- 問題解決能力の向上:統計を用いた問題解決能力が身につくことで、データ分析や意思決定において自信を持って行動できるようになります。
統計検定3級の出題範囲
さて、先ほど扱った範囲について、具体的にはどういう問題が出るのかなどを見ていきましょう。
統計検定3級は、統計の基礎を理解し、データを正しく分析する能力を測る試験です。
| 大分類 | 中分類 |
| 統計学の基礎 | – データの種類(定量データ、定性データ) – 基本的な記述統計(平均、中央値、最頻値) – 散布度の指標(範囲、分散、標準偏差) |
| 確率 | – 確率の定義と基本的な法則 – 条件付き確率と独立性 – 確率分布の種類(正規分布、二項分布など) |
| 推測統計 | – 母集団と標本 – 点推定と区間推定 – 仮説検定の基本概念(帰無仮説、対立仮説) |
| 回帰分析 | – 単回帰分析 – 相関係数の理解 – 回帰方程式の導出と解釈 |
| 統計的データの利用 | – グラフや表の作成 – データの視覚化 |
統計検定3級の出題範囲を把握した上で、効果的な対策を講じることが重要です。
いくつか内容を見ていきましょう。
基礎的な統計量
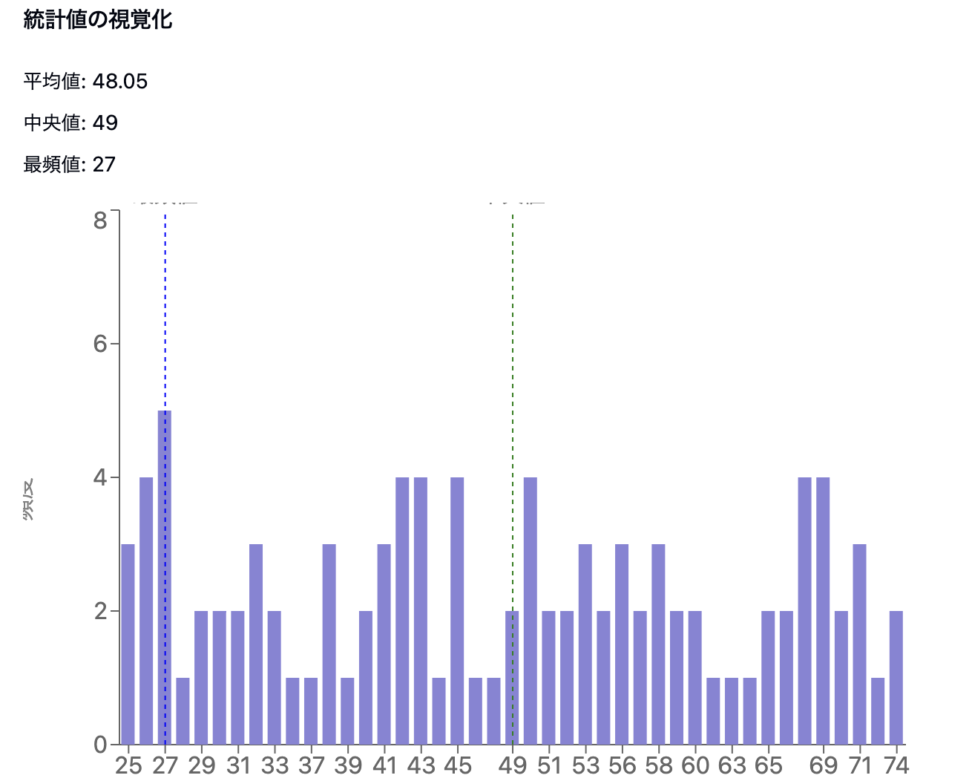
平均値や最頻値に加え、分散などの概念を正しく理解できているかを確認する問題が出題されます。
- 平均値: データの中心的な傾向を示す指標です。
- 中央値: データを昇順に並べた時の中央の値で、外れ値に影響されにくい特徴があります。
- 最頻値: 最も頻繁に出現するデータの値です。
- 分散と標準偏差: データのばらつきを示す指標で、データの散らばり具合を理解するのに役立ちます。
期待値(Expected Value)とは?
期待値とは、ある確率変数がとる値の「平均的な値」を示します。
特定の出来事が起きる確率を考慮した上で、値を予測する際の基準となるもので、確率論における「重み付き平均」とも言えます。
例えば、サイコロを1回振ったときに出る目の期待値を考えてみましょう。サイコロの目は1から6まであり、どの目も等しく出る可能性があります。期待値は次のように計算されます
$${E[X]=\sum_{i=1}^nx_i\cdot P(x_i)}$$
ここで、${E(X)}$ は期待値、${x_i}$ は取り得る値、${P(x_i)}$ はその値が出る確率です。
分散(Variance)とは?
分散は、データのばらつきを示す指標です。データが期待値の周りにどの程度散らばっているかを数値で表し、データが「広がっている」か「集中している」かを知る手がかりになります。分散が大きければデータが広がっていることを意味し、分散が小さければデータが期待値の周りに集中していることを意味します。
分散は次の式で計算されます
$${Var(X)=E[X^2]-(E[X])^2}$$
ここで、${Var(X)}$ は分散、${E(X)}$ は期待値、${X}$は確率変数です。
この式は、データの各値と期待値の差の二乗の平均を求めることで、データのばらつきを数値化しています。
確率
この辺は高校で勉強しているし、わかりやすい概念なので理解しやすいテーマだとは思います。
ただ、分布や「離散や連続」などの概念が入ると話が込み入っていきます。
確率の基本的な考え方は、ランダムな出来事や不確実な状況に対する「予測」を数値化することにあります。確率は0から1の間の値で表され、0は「起こり得ないこと」、1は「必ず起こること」を示します。0.5は「50%の確率」、つまり半分の確率で起こることを意味します。
確率の3つの基本法則
確率にはいくつかの基本的な法則があり、これらはより複雑な確率計算の基礎になります。
加法法則(または和の法則)
互いに排他的な(同時には起こらない)事象 A と B のいずれかが起こる確率は、それぞれの事象の確率を足したものに等しくなります。
$${P(A\cup B)=P(A)+P(B)}$$
乗法法則(または積の法則)
互いに独立した(片方の結果がもう片方に影響を与えない)事象 A と B が同時に起こる確率は、それぞれの確率を掛け合わせたものに等しくなります。
$${P(A\cap B)=P(A)+P(B)}$$
補集合の法則
ある事象 A が起こらない確率は、1 から A が起こる確率を引いたものになります。
$${P(\overline{A})=1-P(A)}$$
確率分布
確率分布は、確率変数の取りうる値とそれに対応する確率を示す関数です。
主な確率分布には以下があります。
離散確率分布
– 例:サイコロの目、コインの表裏
– 代表的なもの:二項分布、ポアソン分布
連続確率分布
– 例:身長、体重などの測定値
– 代表的なもの:正規分布、指数分布
3級では、各分布の特徴や、期待値、分散などの計算方法を習得する必要があります。
推定と検定
統計検定2級にステップアップする上でも、ここは外せないテーマですね。3級だと最も統計学の考え方を理解しないと、なかなか応用問題が解けない分野だと思います。
推定(Estimation)とは?
推定は、ある母集団(例えば、日本全国の人々全体)の特性を知りたいときに、その母集団の一部(サンプル)を使って全体の特性を推測する方法です。
例えば、日本全国の平均身長を知りたい場合、すべての人を調べるのは現実的に困難です。そこで、ランダムに選んだ一部の人たち(サンプル)を調査し、そのデータを基に全国の平均身長を推定します。

当然母集団全体に対して調査を行う(全数調査と言います。国勢調査とか。)のが良いですが、調べたいことによってはコストや時間がかかるので、こうした統計的な手法を使うのです。
推定には大きく分けて2つの方法があります
- 点推定(Point Estimation)
サンプルから得られたデータをもとに、ある1つの値(例えば平均や割合など)で母集団の特性を推定する方法です。例として、サンプル平均を母集団の平均として使うのが一般的です。 - 区間推定(Interval Estimation)
サンプルデータをもとに、母集団の特性が含まれる範囲を示す方法です。推定には必ず不確実性が伴うため、点推定よりも「ある範囲」を提示する方が、より信頼性が高いとされています。例えば、「母集団の平均は95%の確率で1.5mから1.8mの間にある」といった形で示されます。
検定(Hypothesis Testing)とは?
検定は、「ある仮説が正しいかどうか」を統計的に確認する方法です。たとえば、「新しい薬が既存の薬より効果がある」といった仮説が正しいかどうかを検証する際に使われます。検定では、まず「帰無仮説(null hypothesis)」と呼ばれる仮説を立て、サンプルデータをもとにその仮説が統計的に棄却できるかどうかを判断します。
検定の基本的な流れは以下のようになります。
帰無仮説の棄却判断
計算した検定統計量と有意水準を比較し、帰無仮説が棄却されるかどうかを判断します。帰無仮説が棄却される場合、対立仮説が支持されることになります。
帰無仮説(H0)と対立仮説(H1)の設定
帰無仮説は「効果がない」や「差がない」といった仮説で、対立仮説は「効果がある」や「差がある」といった仮説です。
例えば、帰無仮説として「新しい薬と既存の薬に効果の差はない」、対立仮説として「新しい薬は既存の薬より効果がある」と設定します。
有意水準の設定
有意水準は、仮説が棄却されるべき確率の基準を示します。一般的には5%(0.05)が使われることが多く、「5%の確率で誤って帰無仮説を棄却することが許容される」という意味です。
検定統計量の計算
サンプルデータを用いて、帰無仮説のもとで計算される統計量を算出します。この統計量が有意水準を超えると、帰無仮説が棄却され、対立仮説が支持されます。
この分野で出るのが、 「p値」というものです。聞いたことがある方も多いと思います。これは、得られたデータが帰無仮説の下で観測される確率で、p値が事前に設定した有意水準(例: 0.05)以下であれば、帰無仮説を棄却します。
さて、本日はここまで!
統計検定3級は、基礎的な統計学の知識を身につけるための第一歩であり、幅広い分野での応用が期待されます。試験の概要や出題範囲、対策方法を理解することで、合格に向けた確実なステップを踏むことができます。
今後、統計学を学ぶ方々は、ぜひ挑戦してみてください。青の統計学が全力でサポートできると思います。
引き続きよろしくお願いします!
素敵な統計ライフを:)










