【因果推論】uplift modeling(アップリフトモデリング)とは？詳しく解説｜TWO MODELとX LEARNER
こんにちは、青の統計学です。
アップリフトモデリングは、マーケティングや広告などの分野で、特定のアクション（例えば、プロモーションやキャンペーン）が個々の顧客やユーザーに与える影響を予測するための手法です。
このモデルのモチベーションになるのは、アクションがその人にどれだけの「追加的な影響」を与えるかを予測することにあります。
たとえば、SNSオーガニック投稿のROIを試算するときに、自社のSNS経由で予約した人、非経由で予約した人を見て、一人あたりの予約数の差を「オーガニック投稿によるリフト」と言えるでしょうか。
言えないですね。ここには、「SNSを普段から見る人は、もともと予約数が大きい（つまり純粋なオーガニック投稿による影響だけではない）」といった要素を見落としています。正確な因果効果を確認するには、傾向スコア等の補正が必要になります。
なぜUplift Modelingが必要なのか？
従来のA/Bテストの限界
現場では、A/Bテストが広く用いられています。これは、ある施策（介入）が全体にどのような影響を与えるかを評価するための超基本の手法です。例えば、新しい広告キャンペーンが顧客の購買率を向上させるかどうかを検証するために、顧客をランダムに2つのグループ（広告を見せる介入群と見せない対照群）に分け、それぞれの購買率を比較します。もし介入群の購買率が対照群よりも統計的に有意に高ければ、「この広告キャンペーンは効果がある」と判断します。
ABテストについては、この辺が参考になります。
UI/UX 改善における統計的アプローチ： ～サンプリング設計とベイズ推論の活用～
しかし、このA/Bテストには、平均的な効果しか捉えられないという限界もあります。A/Bテストは、あくまで「全体として」施策が有効かどうかを判断するものであり、個々の顧客がその施策によってどのように行動を変えるかまでは教えてくれません。
「個の因果」を捉える重要性
当然ですが、ビジネスでは限られたリソースを最も効果的に配分したいと考えます。全員に施策を行うのはコストがかかりすぎますし、効果のない人に施策を行っても無駄になってしまいますよね。
理想は、「施策を行うことで行動が変化する人」にのみ施策を届けることです。
CRM的な考え方ですね。
ここで重要になるのが、「個の因果」を捉えるという考え方です。
「個の因果」とは、ある特定の個人に対して、もし施策を行った場合と行わなかった場合で、その人の行動がどのように変化するか、という問いです。これは、私たちが通常観測できるデータからは直接知ることができません。なぜなら、私たちはある個人に対して、施策を行った状態と行わなかった状態を同時に観測することはできないからです。
反実仮想というやつですね。しかし、この「もしも」の世界を推測しようとするのが、因果推論の核心であり、Uplift Modelingが目指すところです。
Uplift Modelingは、この「個の因果」を予測し、施策によって行動が向上する可能性のある顧客（Uplift顧客）を特定することを目的としています。これにより、限られた予算の中で、効果的なターゲティングを実現し、ROIを最大化することが可能になります。
因果推論の基本的な考え方から理解したい方は、以下のコンテンツをご覧ください。
思考の転換：誰にアプローチ「しない」べきか
uplift modelingの嬉しさをもう少し具体化しましょう。
従来のマーケティングでは、「誰にアプローチすべきか」という問いに焦点が当てられがちでした。しかし、Uplift Modelingは、それだけでなく「誰にアプローチしないべきか」という、より効率を意識した視点を提供します。
事業の成長フェーズや戦略によっては、財務体質を筋肉質化するような、効率を意識した施策（=ROIを高める）の提案が通りやすかったりします。
Uplift Modelingは、顧客を以下の4つのセグメントに分類します。
### 4つの顧客セグメント
画像挿入ポイント：4つの顧客セグメントを図で表現（介入群で反応、対照群で反応しない、など）
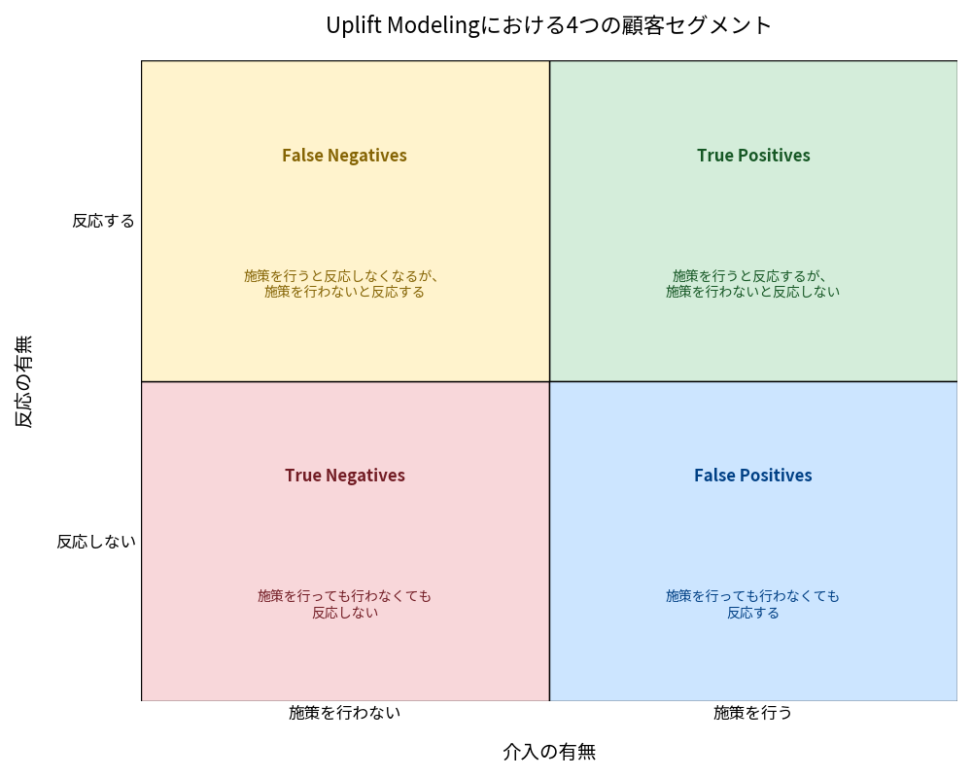
1. True Positives (Persuadables): 施策を行うと反応するが、施策を行わないと反応しない顧客。最もアプローチすべきターゲットであり、Uplift Modelingが最も重視するセグメントです。彼らに施策を行うことで、売上やエンゲージメントの真の「増分（Uplift）」が生まれます。
2. True Negatives (Sure Things): 施策を行っても行わなくても反応しない顧客。アプローチしても無駄なコストがかかるため、アプローチすべきではないセグメントです。
3. False Positives (Lost Causes): 施策を行っても行わなくても反応する顧客。施策を行わなくても反応するため、施策を行うのは無駄なコストとなります。アプローチすべきではないセグメントです。
4. False Negatives (Sleeping Dogs): 施策を行うと反応しなくなるが、施策を行わないと反応する顧客。天邪鬼みたいですね。アプローチしてはいけないセグメントです。施策を行うことで、かえって顧客を失うリスクがあります。
４ですが、執拗なテレマーケティングなど、顧客の信頼を損なったり、うざったいマーケ手法だと４の割合が増えそうですね。自分の担当していたキャンペーン案件では、テレマーケティングで、増分コンバージョンがマイナスになっていたので４の可能性を感じました。
Uplift Modelingは、この4つのセグメントのうち、特に「True Positives (Persuadables)」を特定し、彼らにリソースを集中させることを可能にします。同時に、「False Negatives (Sleeping Dogs)」のような、施策によって悪影響を受ける可能性のある顧客を避けることで、ネガティブな影響を最小限に抑えることができます。これは、限られた予算の中で最大の効果を生み出すための、より洗練されたアプローチです。
Uplift Modelingの数学的背景
Uplift Modelingを理解するためには、まず因果推論の基本的な枠組みである「潜在的アウトカムフレームワーク」を理解することが不可欠です。これは、個の因果効果を数学的に定義するための基礎となります。
まずは、ここから考えていきます。
潜在的アウトカムフレームワーク
潜在的アウトカムフレームワーク（Potential Outcomes Framework）、またはルービン因果モデル（Rubin Causal Model）は、統計的因果推論の基本的な考え方の一つです。このフレームワークでは、各個人に対して、もし介入（施策）を受けた場合の結果と、もし介入を受けなかった場合の結果という2つの「潜在的アウトカム」が存在すると仮定します。
ある個人$i$について、
- 介入を受けた場合の潜在的アウトカムを $Y_i(1)$ とします。
- 介入を受けなかった場合の潜在的アウトカムを $Y_i(0)$ とします。
個人$i$に対する介入の因果効果（Individual Treatment Effect, ITE）は、この2つの潜在的アウトカムの差として定義されます。
$${ITE_i = Y_i(1) – Y_i(0)}$$
Uplift Modelingは、この $ITE_i$ を個々の顧客レベルで推定しようとする試みであると言えます。しかし、前述の通り、$Y_i(1)$ と $Y_i(0)$ の両方を同時に観測することはできないため、直接 $ITE_i$ を計算することは不可能です。
そこで、統計的な手法を用いて、この $ITE_i$ を推測することになります。
CATE (Conditional Average Treatment Effect) の定義
個々の $ITE_i$ を直接推定することは困難ですが、特定の属性を持つグループにおける平均的な因果効果を推定することは可能です。これを条件付き平均処置効果（Conditional Average Treatment Effect, CATE）と呼びます。CATEは、共変量（顧客の属性など）$X$ が与えられた条件下での平均的な因果効果として定義されます。
$${CATE(x) = E[Y(1) – Y(0) | X=x]}$$
Uplift Modelingでは、この $CATE(x)$ を推定し、それが正の値（施策によって行動が向上する）となるような顧客セグメントを特定することを目指します。つまり、Uplift Modelingは、顧客の属性 $X$ に応じて、施策の効果がどのように異なるかを予測するモデルでというわけです。
Uplift Scoreの導出
Uplift Modelingにおける「Uplift Score」は、CATEの推定値、またはそれに準ずる指標として用いられます。このスコアが高いほど、その顧客に施策を行うことで行動が向上する可能性が高いと判断されます。Uplift Scoreを導出するアプローチはいくつか存在しますが、ここでは代表的なものを紹介します。
Two-Modelアプローチ
最も直感的で理解しやすいのがTwo-Modelアプローチです。これは、介入群と対照群それぞれに対して、目的変数（例：購買有無）を予測するモデルを構築し、その予測値の差をUplift Scoreとする方法です。
- 介入群モデルの構築: 介入群のデータを用いて、顧客の属性 $X$ から介入後のアウトカム $Y(1)$ を予測するモデル $M_1$ を構築します。
- ${P(Y=1|X, T=1)}$
- 対照群モデルの構築: 対照群のデータを用いて、顧客の属性 $X$ から介入なしのアウトカム $Y(0)$ を予測するモデル $M_0$ を構築します。
- ${P(Y=1|X, T=0)}$
そして、Uplift Scoreは、介入が与えられた場合と与えられなかった場合で、目的の行動変化が起こる確率の差を示しています。
$${Uplift Score(x) = P(Y=1|X=x, T=1) – P(Y=1|X=x, T=0)}$$
Yに影響を与えそうな条件を所与にして、純粋な効果を見て行こうというわけですね。
理解しやすいですね。このアプローチの利点は、既存の分類モデル（ロジスティック回帰、決定木、ランダムフォレストなど）をそのまま利用できる点です。
しかし、欠点としては、2つのモデルの予測誤差がUplift Scoreに累積されることや、直接因果効果をモデリングしているわけではないため、推定の精度が低い場合がある点が挙げられます。
分類問題とのモチベーションの違い
通常の分類問題は、ある入力データ $X$ が与えられたときに、そのデータがどのクラスに属するか（例：顧客が購買するかしないか）を予測することを目的とします。つまり、${P(Y=1|X)}$ を推定します。しかし、Uplift Modelingが予測したいのは、**施策の有無による行動の変化**、すなわち ${P(Y=1|X, T=1) – P(Y=1|X, T=0)}$ です。
これは、単に購買するかどうかを予測するだけでは不十分であることを意味します。
例えば、ある顧客が「広告を見せても見せなくても購買する」タイプだったとします。通常の分類モデルは、この顧客が購買することを予測するでしょう。しかし、Uplift Modelingの観点からは、この顧客に広告を見せることは無駄なコストであり、むしろ「広告を見せなくても購買する」という特性を活かして、別の施策を検討すべき対象となります。このように、Uplift Modelingは、予測だけでなく、**意思決定のための示唆**を与える点に特徴があります。
Meta-Learners (S-Learner, T-Learner, X-Learner)
Two-Modelアプローチ以外にも、Uplift Modelingには様々な手法が存在します。
これらは、Two-Modelアプローチをより洗練させたもので、異なる戦略でCATEを推定します。例えば、S-Learnerは単一のモデルで全てを学習し、T-LearnerはTwo-Modelアプローチの拡張版、X-Learnerはより複雑な状況に対応するために開発された手法です。
Meta-Learners
* **S-Learner (Single Learner)**: 介入変数 $T$ を通常の共変量として扱い、単一のモデルで ${E[Y|X, T]}$ を学習します。そして、${CATE(x) = E[Y|X=x, T=1] – E[Y|X=x, T=0]}$ を計算します。シンプルですが、モデルが因果効果を適切に学習できるかどうかが鍵となります。
T-Learner (Two Learner): Two-Modelアプローチと同様に、介入群と対照群でそれぞれ独立したモデル ${M_1(X) = E[Y|X, T=1]}$ と ${M_0(X) = E[Y|X, T=0]}$ を学習します。その後、${CATE(x) = M_1(x) – M_0(x)}$ を計算します。Two-Modelアプローチとの違いは、CATEの推定に特化した損失関数や最適化手法を用いることで、より精度の高い推定を目指す点にあります。
X-Learner (Cross Learner): T-Learnerの拡張であり、特に介入群と対照群のサンプルサイズに偏りがある場合に有効です。まず、T-Learnerと同様に ${M_1(X)}$ と ${M_0(X)}$ を学習します。次に、それぞれのモデルの予測値を用いて、観測されていない潜在的アウトカムを推定し、その推定値からCATEを学習する第2段階のモデルを構築します。これにより、データが少ないグループからの情報も活用し、よりロバストなCATE推定が可能になります。
備考：介入とランダム化について
「介入」とは、ある原因となる変数（処置変数、T）の値を意図的に操作することを指します。例えば、施策における「広告を見せる」「クーポンを配布する」といった行為が介入にあたります。当然ですが、介入はその結果として生じるアウトカムの変化を観察するために行われます。
一番重要なのは、介入がランダムに行われること、あるいはランダムに行われたと見なせる状況を作り出すことです。これにより、交絡因子の影響を排除し、介入とアウトカムの間の純粋な因果関係を特定することが可能になります。
因果推論において、信頼性の高い因果効果の推定方法とされているのが、ランダム化比較試験（Randomized Controlled Trial, RCT）です。RCTでは、対象となる人々をランダムに2つ以上のグループに分けます。一方のグループには介入を行い、もう一方のグループには介入を行わないか、別の介入を行います。
ランダムにグループ分けすることで、介入群と対照群の間で、観測可能な属性（年齢、性別など）だけでなく、観測できない属性（健康意識、購買意欲など）も平均的に均等になります。これにより、介入群と対照群のアウトカムの差は、ほぼ純粋に介入による効果であると見なすことができます。つまり、RCTは、反事実の世界をシミュレートするための手段というわけです。
Uplift Modelingは、理想的にはRCTによって収集されたデータを用いることで、その真価を発揮します。RCTデータがあれば、介入群と対照群の比較が因果効果の推定に直結するため、より正確なUplift Scoreを導き出すことが可能になります。
