【統計検定準一級】ランダムウォークとマルチンゲールの話。
こんにちは、青の統計学です。
統計検定準一級では、「この確立過程Sは、マルチンゲールかどうか?」という問題が出ることがあります。
マルコフ性と並んで登場する「マルチンゲール」に、とっつきにくさを感じた方も多いと思います。
ここでは、マルチンゲールとその例としてランダムウォークを学んでいきましょう。
統計検定のチートシートは以下をクリック!
【最短合格】統計検定準一級のチートシート|難易度や出題範囲について
【最短】統計検定2級合格ロードマップとチートシート|おすすめの本について
マルチンゲール
以下の条件をもつ確率過程を、「マルチンゲール」と呼びます。
ただし、Yは整数値をとる確率変数(あるいは確率ベクトル)であるとします。
$$E[Y_{n}|Y_{n-1},..,Y_{0}]=Y_{n-1}$$
時点n-1における時点nのYの条件付き期待値(上の式)は、時点n-1のYと同様に確からしいということです。
砕けた言い方だと、n-1回目までの試行の情報を使って、n回目の試行を行った時の事象の期待値は、n-1回目の事象と同様であるということです。
期待値の特性も含め、以下のような特性を持つ確率過程\(X_t\)をマルチンゲールと呼びます。
・ X_t は適応的(adapted)である:時刻tにおいて、X_t の値は t までの情報を用いて予測できる。
・ X_t は有界である:ある時刻tまでの値が有界であるということ。
・ 条件付き期待値が一定である:すべてのtとs(t < s)に対して、\(E[X_s | X_t] = X_t\) が成り立つ。
これは、過去の情報を知っていても、未来の期待値は現在の値と同じであることを意味します。
ポアソン過程がマルチンゲールかどうかについての話は、こちらが参考になります。
CODE|python
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
def fair_coin_toss(n_tosses):
tosses = np.random.choice([-1, 1], size=n_tosses)
return np.cumsum(tosses)
#1000回コインを投げるという試行を
n_tosses = 1000
#10回繰り返す
n_paths = 10
plt.figure(figsize=(12, 6))
for i in range(n_paths):
path = fair_coin_toss(n_tosses)
plt.plot(range(n_tosses), path, label=f"Path {i+1}")
plt.xlabel("Number of Tosses")
plt.ylabel("Cumulative Sum")
plt.title("Martingale Example: Fair Coin Toss")
plt.legend()
plt.grid()
plt.show()
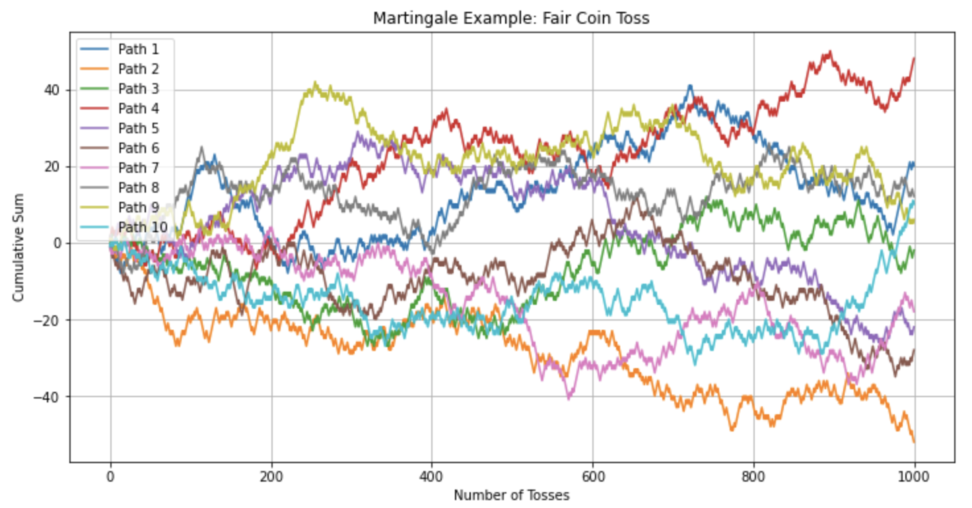
マルチンゲールの様子を見てみましょう。
このように図示すると、10個の異なるマルチンゲール過程が表示されます。
フェアなコイン投げの場合、過去の結果から未来の結果を予測することはできませんが、累積の変化を視覚的に確認することができます。
ランダムウォーク
中学校の数学がわかっていれば、理解ができると思います。以下の例をご覧ください。
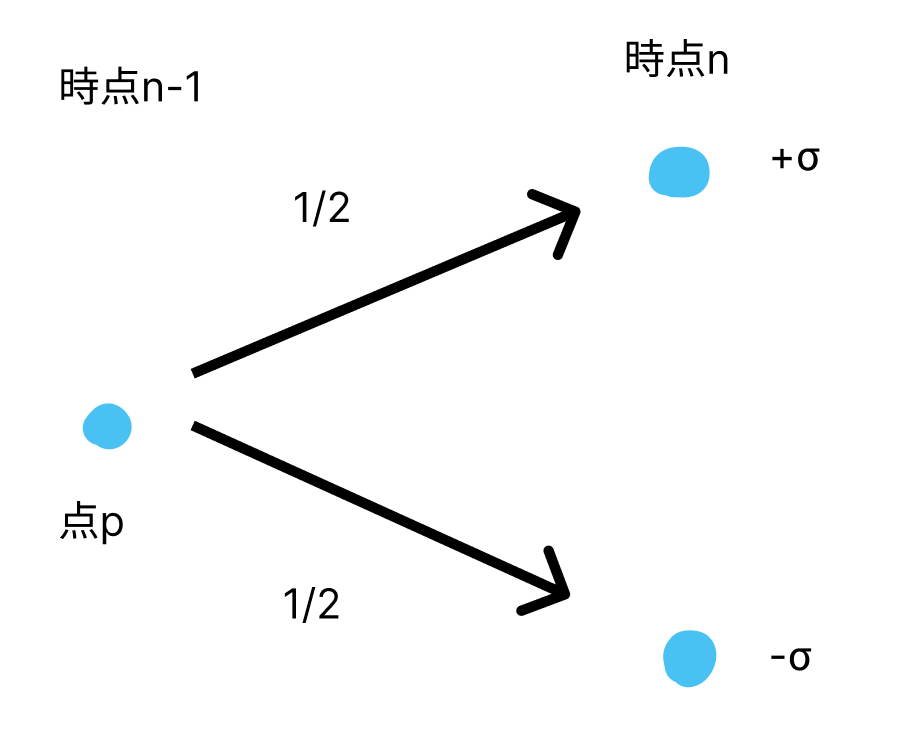
点Pが1秒ごとに1/2の確率でy座標が+σに動き、1/2の確率で-σに動くとします。 スタートは原点(0,0)です。 時点tにおける点Pの座標をr(t)とする時、r(t)をランダムウォークと呼びます。 r(t)の期待値と分散を求めてみましょう。
期待値
まずは変化率を考えます。
$$Δr(t)=r(t+1)-r(t)$$
時点t+1と時点tでの差で表すことができます。
ランダムウォークなので、\(\frac{1}{2}\)で+σ、\(\frac{1}{2}\)で$${-\sigma}$$になるので期待値としては0になります。
$$E[Δr(t)]=0$$
\(r(t)\)は、時点1からのランダムウォークの変化率であると考え、以下のように期待値の和を考えます。
$$E[r(t)]=E[Δr(1)+Δr(2)+…+Δr(t)]=E[Δr(1)]+…+E[Δr(t)]$$
結局は0のt回足し算になるので、ランダムウォークの期待値は0になります。
分散
同じく変化率の分散からいていきましょう。
分散:(2乗の平均)-(平均の2乗)
を使います。
とはいえ、第2項は0になります。\(\sigma^2\)になります。
$$V(Δr(t))=σ^2$$
$$V(r(t))=V(r(Δ1)+..+r(Δt))=V(r(Δ1))+..+V(r(Δt))$$
和の分散は分散の和になります。先ほどのように\(\sigma^2\)を\(t\)回足したものになります。
よって、ランダムウォークの分散は\(\sigma^{2}t\)になります。
$$V(r(t))=\sigma^{2}t$$
時間が経てば経つほど、ばらつきが増えるということになります。
期待値は0で、分散は\(\sigma^{2}t\)になることがわかりました。
補足|MCMC法のメトロポリスヘイスティングアルゴリズムとランダムウォーク
事後分布のサンプリングのためのアルゴリズムの一つとして、メトロポリスヘイスティングアルゴリズムがあります。
そこでパラメータを更新するときに、現在→1期前のパラメータに遷移する確率と1期前→現在のパラメータに遷移する確率が等しい、つまりランダムウォークである場合があります。
詳しくは以下のコンテンツをご覧ください。
【完全ガイド】MCMC法についてわかりやすく解説|ベイズ推定
マルチンゲールとランダムウォーク
ランダムウォークは、マルチンゲールの性質が成り立ちます。
つまり、\(Y_{n}\)の辿る過程は、過去の情報であるY1‥が与えられた時に、以下が成り立つことになります。
$$E[Y_{n}|Y_{n-1},…,Y_{0}]=Y_{n-1}$$
当然ですが、ランダムウォークは時点n-1においてこれまでの情報をいくら利用しても+1になるか-1になるかの確率は1/2です。
時点nの期待値が増加する確率も減少する確率も同様に確からしいということになります。
少し統計とは脱線しますが、株価の動きが「ランダムか否か」という議論があります。
この時の「ランダム派」である、「過去の情報をいくら利用しても、次の事象については何もわからない」というランダムウォーク理論は、以下の3つの要素で成り立ちます。
1:利用可能な情報が全て市場に反映される
2:市場参加者は全員合理的な行動をとる
3:取引コストがかからない
これが成り立つ市場を「効率的な市場」と呼んでいます。あまり現実的ではないですね。
マルチンゲール戦略
マルチンゲールの性質を持つ戦略として、マルチンゲール戦略があります。
よく「ギャンブルの必勝法!?」などと呼ばれている方法ですが、実態はその逆で「必ず負ける方法」です。
以下の事例をみてみましょう。
Aさんは、「買ったら掛けた額と同じ額を得られる」コイン投げの賭け事に参加しました。 Aさんは、マルチンゲール戦略を取ります。負け続ける限り、k回目の掛け金はk-1回目の掛け金の2倍です。 そして、勝つまでやります。 最初の掛け金は1円です。
状況としては、
- オッズ2倍の馬券を買った
- ブラックジャック
- ルーレット
などと同じです。
マルチンゲール戦略とは、「負け続ける限り、掛け金を2倍にしていく方法」です。
勝つまで掛けることで、お金を回収できるというものです。
こういう戦略から、倍々法や倍追法と呼ばれています。
1 , 2 , 4 , 8 ,‥,とかけていきます。n-1回目まで負け続けると、損失額は下の通りです。
$$2^0+2^1+..+2^{n-1}=2^n-1$$
では、めでたいことにn回目で勝ったとしましょう。マルチンゲール戦略に基づき、n回目は\(2^n\)かけているので、\(2^n\)円getしました。
$$2^n-(2^{n-1}-1)=1$$
これまでの損失額と今回獲得した金額の差は+1円になります。
なので、必勝法と呼ばれています。どこがおかしいでしょうか?
なぜ必ず負けるのか?
一見負けがないように見えるマルチンゲール戦略ですが、実は真逆です。
まず、\(n-1\)回目で負けた時にn回目ではその2倍掛けるというのが、予算上厳しいからです。
例えば、1回目の掛け金が1万円だった時に、10回目の掛け金は2の10乗で1024万円かける必要があります。
次に、マルチンゲールの性質を振り返って考えてみると、「次に掛ける」期待値が「今の所持金」を上回らないことがわかります。
$$E[Y_{n}|Y_{n-1},…,Y_{0}]=Y_{n-1}$$
マルチンゲールの性質を持つので、「現在の持っているお金」と「次にゲームをやった後の持ち金の期待値」が等しいです。つまり、やっても意味がありません。
マルチンゲールの性質を持つ、というのは「\(n-1\)回目までの掛け金の情報を使っている」ところにあります。
これが、今までの結果という条件を持つ、条件付き期待値となる理由です。
①予算が無限にないと成立しない
②マルチンゲールの性質上、次の期待値が今の所持金を超えない。
以上の2点より、マルチンゲール戦略は必ず破綻すると言われています。
マルチンゲールの判断
最後に少し難しい例題を解いてみましょう。
マルチンゲールかどうかを判定する問題です。
条件:
n=0,1,2,3,4‥に対して、Xnは整数値を取る確率変数とします。
Xn = i となった時に Xn+1 = jとなる確率pi,jは、nに依存しないとします。
また、X0 = 0 となる確率は 1であるとします。
以下、数式を条件で加えています。
$$p_{i,j}=P(X_{n+1}=j|X_{n}=i)$$
$$p_{i,i+1}=p_{i,i-1}=\frac{1}{2},p_{i,j}=0,i=0,±1,±2,…$$
問題
$$T_{0}=X_{0},T_{1}=X_{1},T_{n}=T_{n-1}+T_{n-2}(X_{n}-X_{n-1})$$
この確率過程\(T_n\)がマルチンゲールかどうかを判定しなさい。
解説
ちょっと自己回帰モデルに似ていますね。
気づいた方も多いと思いますが、\(P_{i,j}\)は「ランダムウォーク」になっています。
「この確率過程はマルチンゲールかどうか」と問われたときは、とにかくマルチンゲールであると仮定して、式に当てはめてみましょう。
今回は確率過程\(T_n\)について聞かれているので。
$$E[T_{n}|T_{1},T_{2},…,T_{n-1}]=T_{n-1}$$
この式が成り立てば、マルチンゲールです。
つまり、条件で置かれていた右辺の第二項\((X_n – X_{n-1})\)の条件付き期待値が0になれば良さそうです。
条件式をよくみてほしいですが、\(T_{n}\)を求める際に\((X_n – X_{n-1})\)という情報が使われているだけで、\((X_n – X_{n-1})\)を求める際には、\(T_{n-1}\)から\(T_1\)までの情報は使われていません。
$$T_{0}=X_{0},T_{1}=X_{1},T_{n}=T_{n-1}+T_{n-2}(X_{n}-X_{n-1})$$
よって、\((X_n – X_{n-1})とT_{n-1},‥,T_1\)は独立ですので、以下の条件付き期待値は0になります。
$$E[X_{n}-X_{n-1}|T_{1},T_{2},…,T_{n-1}]=0$$
よって、右辺の第二項が0になるので、確率過程\(T_{n}\)はマルチンゲールであるといえます。
$$E[T_{n}|T_{1},T_{2},..,T_{n-1}]=T_{n-1}$$




