【周期性を掴もう】pythonでコレログラムを書いてみましょう
ヒストグラムや折れ線グラフなどはよく耳にしますが、「コレログラム」は聞いたことがないかたも多いと思います。
今回は統計検定2級や準一級でよく出る「コレログラム」についてまとめてみました。
統計検定のチートシートは以下をクリック!
【最短合格】統計検定準一級のチートシート|難易度や出題範囲について
【最短】統計検定2級合格ロードマップとチートシート|おすすめの本について
コレログラム
コレログラムとは、「時系列グラフから周期を見つけるための図」です。
今回扱うデータは、気象庁のデータです。
とはいえ、最初はデータ整形を行いましょう。
コレログラムだけを理解したい方は、コンテンツ中盤まで飛んでいただければと思います。
データ整形
2019年1月1日から2022年1月1日までの、 ・平均気温 ・平均湿度 ・日照時間 を日毎に集計しました。
import pandas as pd
temperament = pd.read_csv("data.csv",encoding="shift-jis",skipinitialspace=True)
temperament.head()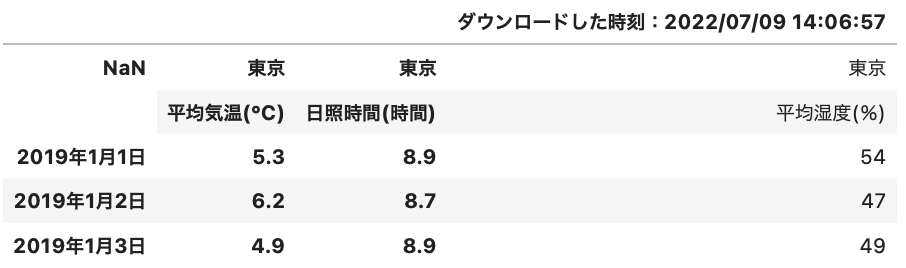
なんと、列名がないことがわかりました。
列名をつけるために、一旦列の数だけ列名を「0,1,2,3‥」とナンバリングしたcsvを作ります。
header=None をつけないと、1行目の内容がそのままキーに来ることがあるので注意です。
temperament.to_csv("temperament.csv")
newTemperament = pd.read_csv("temperament.csv",header=None)次に、列名(Key)を具体的につけてあげます。
列名をつけてあげないと、列名を使った操作の時「Keyerror」というエラーが出てきます。
labels = ["date","temperature", "sunshineTime", "humidity"]
labels_dict = {num: label for num, label in enumerate(labels)}
newTemperament = newTemperament.rename(columns = labels_dict)
# カラム名を追加したデータフレームをcsvファイルとして保存する。
newTemperament.to_csv("newTemperament.csv", index=False)
newTemperament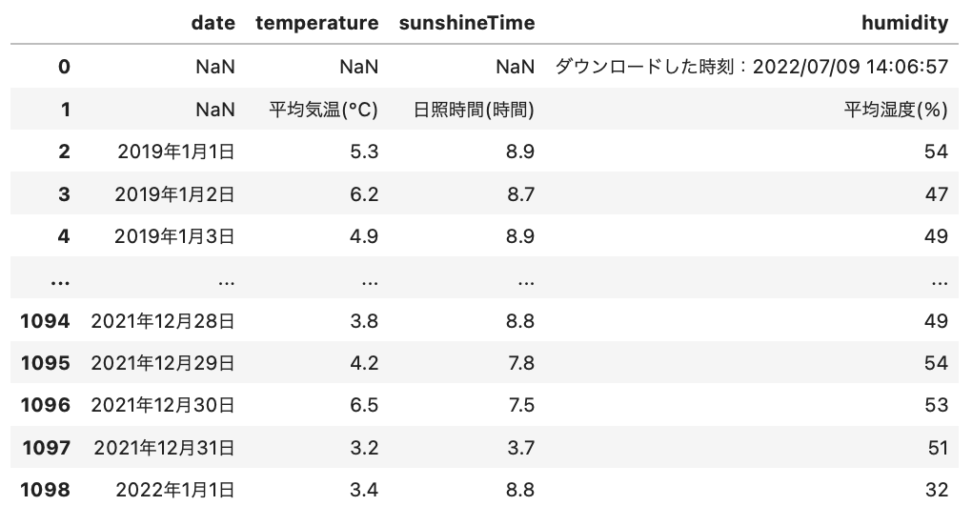
では最後に、いらない1行目と2行目を削除して出来上がります。
整形したcsvを新たに「tokyoTemperament.csv」という名前にして保存します。
#一行目と二行目を削除して、新しくcsvファイルを作る。
realTemperament = pd.read_csv("newTemperament.csv")
realTemperament = realTemperament.drop(index=realTemperament.index[[0,1]])
realTemperament.to_csv("tokyoTemperament.csv",index=False)
tokyoTemperament = pd.read_csv("tokyoTemperament.csv")
tokyoTemperament| date | temperature | sunshineTime | humidity | |
| 0 | 2019年1月1日 | 5.3 | 8.9 | 54 |
| 1 | 2019年1月2日 | 6.2 | 8.7 | 47 |
| 2 | 2019年1月3日 | 4.9 | 8.9 | 49 |
| 3 | 2019年1月4日 | 5.1 | 8.9 | 59 |
| 4 | 2019年1月5日 | 7.4 | 8.9 | 52 |
| … | … | … | … | … |
変化量の計算など
では、ここから時系列特有の計算をしていきましょう。
前日との気温の差を見たい時に、diff()をつかいます。新しく列を作ってみましょう。
#邪魔な値があったので消します。
tokyoTemperament = tokyoTemperament.replace(")","")
tokyoTemperament = tokyoTemperament.replace(']', '')
#float型に変換してからdiff()を使う。
tokyoTemperament["temperature"]= tokyoTemperament["temperature"]).astype(float)
tokyoTemperament["temperature_diff"] = tokyoTemperament["temperature"].diff()
tokyoTemperament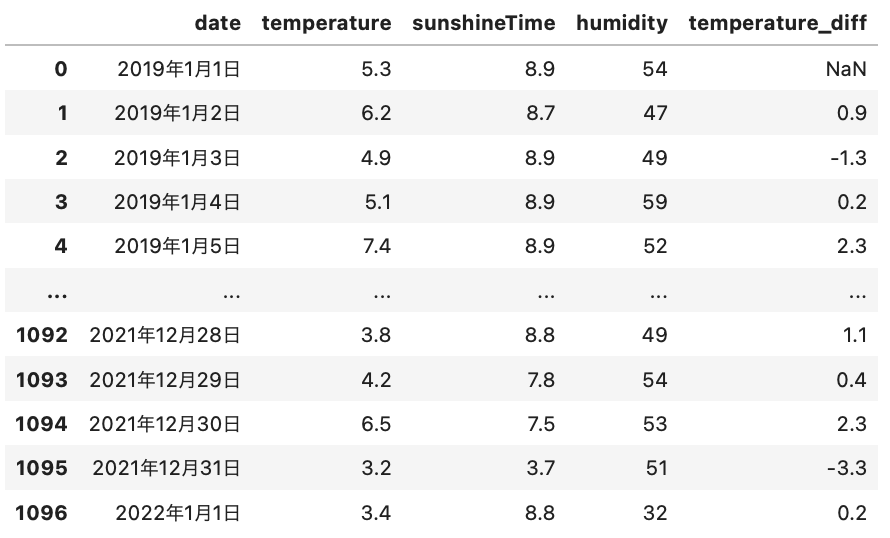
このように気温の差分が最後の列に出てきました。
diff()はデフォルトで1日差になっています。二日前と差を取りたい場合は、diff(2)としてあげればよいです。
よく時系列解析で階差は使われますが、下のようにノイズが2つ残ることになるのでかえってモデルを複雑にすることがあり、注意です。
$$y_n=a+b_n+ε_n$$
こちらが元のモデルです。
$$Δy_n=b+ε_n-ε_{n-1}$$
こちらが1階階差
$$Δ^2y_n=ε_n-2ε_{n-1}+ε_{n-2}$$
こちらが2階階差
さて、データを取り始めた2019年1月1日の「気温の前日差」は当然欠損値として扱われていますね。
次は変化量の計算をしてみましょう。
tokyoTemperament["temperature_cRate"] = tokyoTemperament["temperature"].pct_change()
tokyoTemperament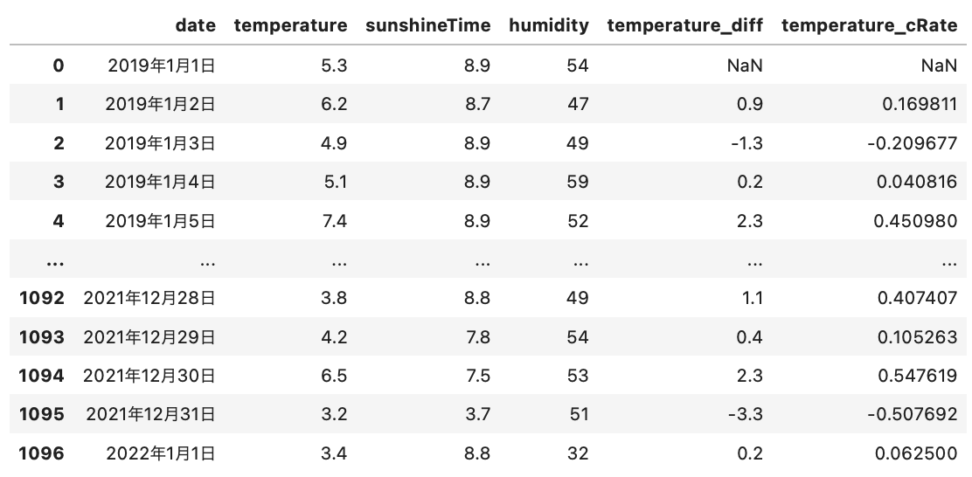
変化量には、pct_change()を使います。使い方やデフォルト値に関しては、diff()と変わらないので割愛します。
例えば、temperature_cRateが、0.169811なら前日よりも16%くらい気温が上がったということになります。
最後に、shift()を使って一日ずらしたデータを見てみましょう。
tokyoTemperament["temperature_move"] = tokyoTemperament["temperature"].shift()
tokyoTemperament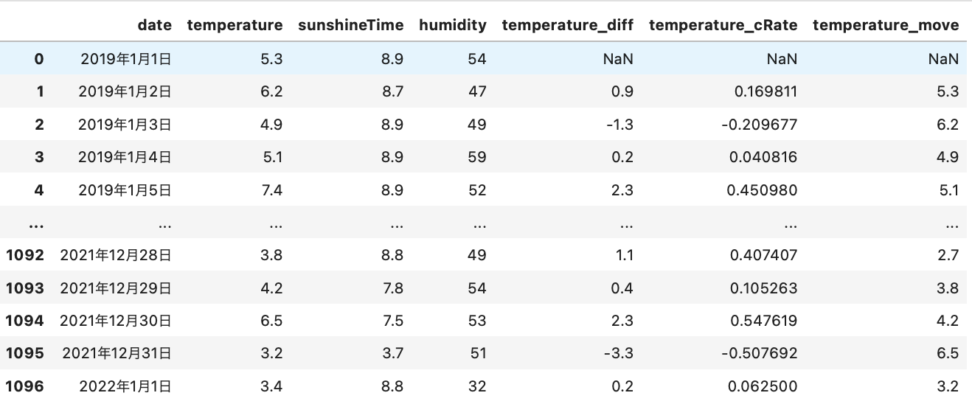
このように、1日だけ気温をずらした列が作れました。shift(365)とすれば、一年前の気温と今の気温が同じ行に入るということになります。
これでコレログラムを学ぶ準備ができました。次は自己相関について解説します。
自己相関とコレログラム
自己相関は、【時系列】ARモデルをわかりやすく解説|Yule-Walker法や最尤法もでも扱いましたが、時期の違うデータの影響を受けて今のデータが変化することを言います。
今回の気象データで言うと、365日前のデータはかなり現在のデータと自己相関係数が高いと予想ができますが、半年前のデータとはあまり関係があるようには考えられません。(逆に負の相関はあるかもしれません)
import statsmodels.api as sm
res = sm.graphics.tsa.plot_acf(tokyoTemperament["temperature"],lags=1000)
res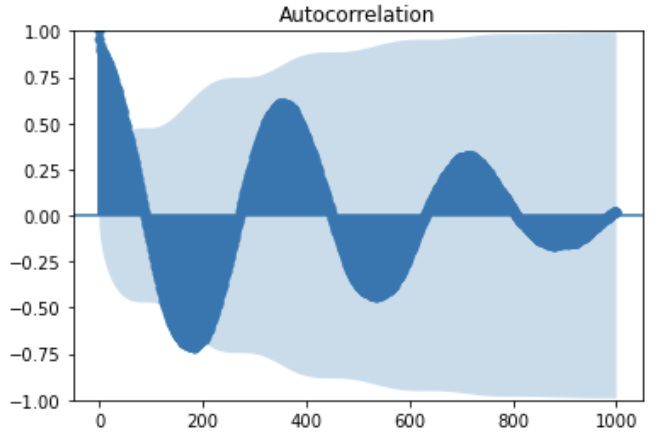
statsmodelsというライブラリを使うとこんなにも簡単にグラフが書けます。
実は、これがコレログラムです。
コレログラムとは、時期をずらしたデータと今のデータの縦軸の相関を測っています。
相関係数が1に近いほど、そのずらした分だけの周期性があると言えます。
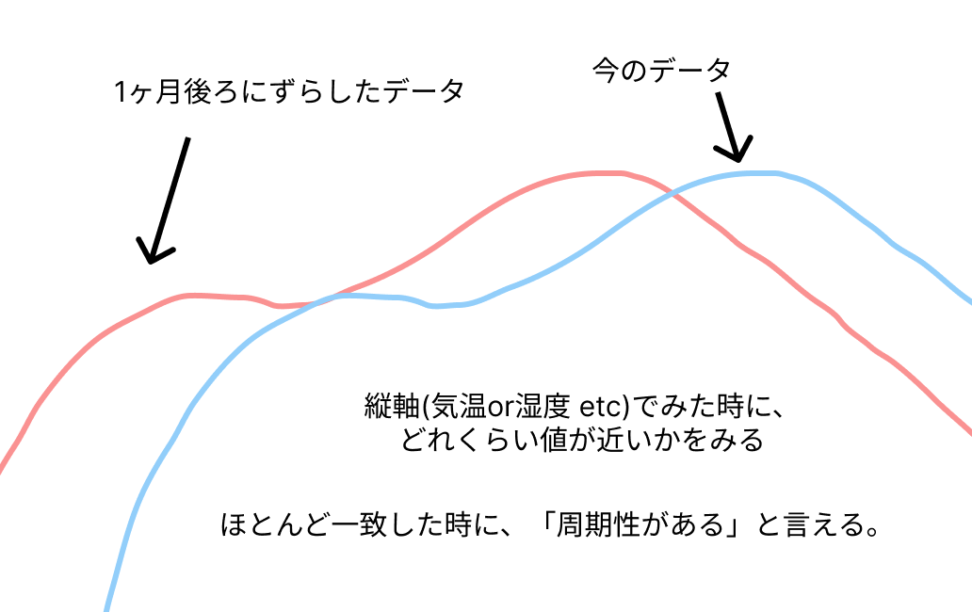
この周期性という考え方は、景気動向や気象情報などを中心に使われます。気温なら一年時期をずらしたデータとほぼ一致すると想像しやすいでしょう。
一方で、発展途上国のGTPのような、大体右上がりのデータだと、「ずらし」をとったとしても値が離れるばかりで、「周期性はない」と考えられます。
(相当期間が長いデータだと周期はあるかもしれませんが、国の名前が変わったりデータが欠損している可能性が高そう)
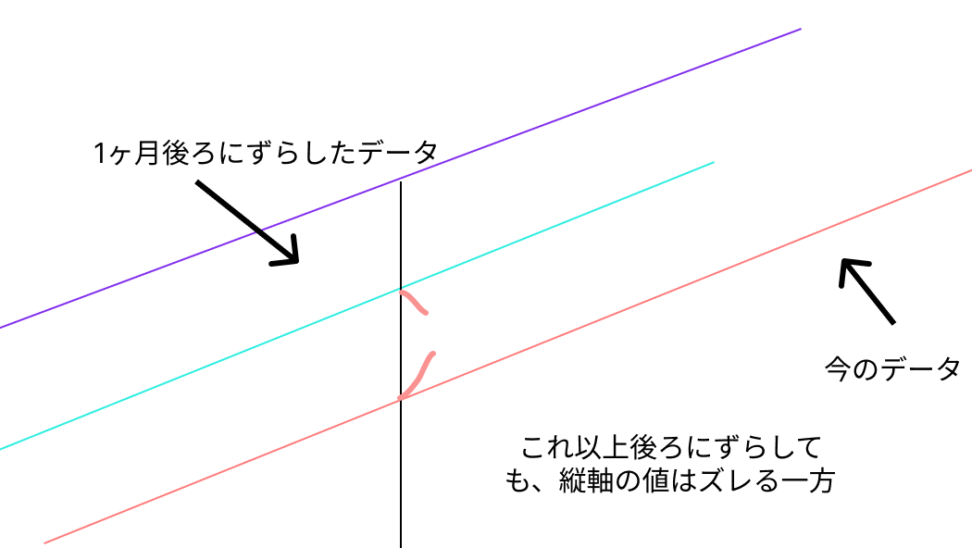
急落や急上昇がない限り、ずらしが小さければ小さいほど自己相関係数は高くなりますが、周期性を探すことが目的なので、それほど価値はないです。
さて、先ほどのグラフを見る限り、「東京の気温」は一年周期で自己相関係数は高くなることがわかりました。
では自己相関係数を定量的にみてみましょう。
sm.tsa.stattools.acf(tokyoTemperament["temperature"],nlags=365)[365]値が多すぎるのでnlags=365までにしました。出力結果は、
0.5972618685753209
となりました。
波形分解
おまけです。
波形分解とは、「周期性の効果を除いた時に全体としてどんな傾向が残っているのか調べる」方法です。
sm.tsa.seasonal_decompose(tokyoTemperament["temperature"].values,period=365).plot()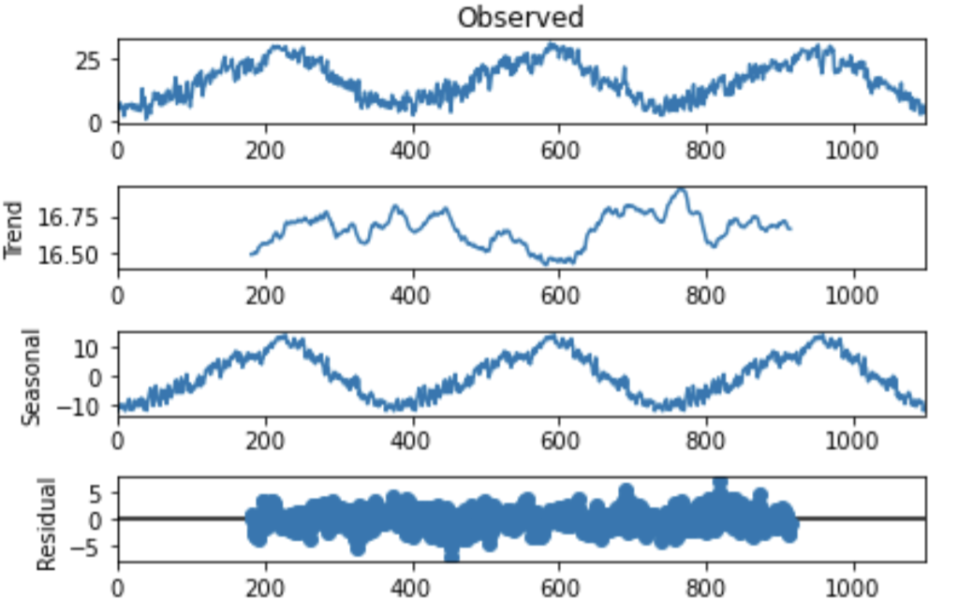
前提として、周期が365日であるということをコレログラムからわかっておく必要があります。
周期は、period= で入力します。statmodelのバージョンによっては、periodがfreqだったりします。
みてほしいのは、2番目と3番目のグラフです。3番目のグラフは、「観測したデータから、周期性のみを抽出したグラフ」です。当然365日周期で綺麗に自己相関係数が上がっていることがわかります。
2番目のグラフは、「観測したデータから、周期性を除いたグラフ」です。
言い換えると、「トレンド」です。
トレンドを見る限り、2020年は平年よりちょっと寒かったようですね。
波形分解とは、観測データから周期性とトレンドを分解する方法でした。余力のある方は覚えておきましょう。


