【統計学】ポアソン分布についてわかりやすく解説
ポアソン分布(poisson distribution)
統計学および確率論で用いられるポアソン分布とは、ある事象が一定の時間内に発生する回数を表す離散確率分布です。
定数\( \lambda > 0\) に対し、\(0\) 以上の整数を値にとる確率変数\(X\)が特定の条件を満たすとき、確率変数\(X\) は母数\(\lambda\) のポアソン分布に従うと言います。
ポアソン分布は、現実の多くの現象をモデル化するのに適しています。
例えば、1分間のWebサーバへのアクセス数や、一定期間内に起こる交通事故の数などは、ポアソン分布によってモデル化することができます。
・交通事故に遭う確率
・火事が発生する確率
などの確率分布にポアソン分布は使われます。
確率\(p\)が限りなく\(0\)に近く、観測数\(N\)が極めて大きいことを必要としています。
このような特徴を持つ二項分布を、特にポアソン分布と呼んでいます。
数学的背景
分布関数は以下のようになります。
$$p(x)=\frac{\lambda^x}{x!}e^{-\lambda}$$
\(x\):稀な現象が起きる数。0,1,2,3,4と離散的な数です。
\(\lambda\):生起率、強度(intensity)と呼ばれる。稀な現象が単位時間あたりに起きる回数の平均を表しています。
\(e\):自然対数の底。
このポアソン分布が使われる確率過程「ポアソン過程」については以下のコンテンツでご覧ください。
[例題1]
ある町の1日あたりの交通死亡発生数は\(\lambda=1\)のポアソン分布に従います。次の確率を求めなさい。
(1)少なくとも一件の交通事故が発生する確率
(2)多くても一件しか発生しない確率
(1)1から交通事故が一件も起きない確率を引けば良いです。
\(P(x=0)=e^{-1}\)です。
(2)求める確率は、「多くても一件」なので、\(P(x<=1) = P(x = 0) + P(x = 1)\)です。
\(P(x = 0)\)は(1)で求めたように、\(e^{-1}\)でした。
同じように、\(\lambda=1,x=1\)を分布関数に代入すると、\(P(x = 1) = e^{-1}\)となります。
よって求める確率は、\(2e^{-1}\)です。
期待値と分散(expectation & variance)
結論としては、期待値も分散も\(\lambda\)(生起率)です。
数式で書くと、\(E[X] = Var(X) = \lambda\) というわけです。
[例題2]
確率変数Xがポアソン分布\(Po(\lambda)\)に従うとする。
(1)\(\mu = E[X]とE[X(X-1)]\)を求めなさい。
(2)\(Var(X) = E[X(X-1)] + \mu -\mu^2\)になることを示し、\(Var(X)\)を求めなさい。
[解説]
(1)まず期待値は、このように0から無限大までの確率の和に\(x\)をかけてあげます。
$$E(X)=\sum_{x=0}^{\infty}x\frac{\lambda^x}{x!}e^{-\lambda}$$
次に、かけた\(x\)を使って\(x!\)を\((x-1)!\)に約分してみましょう。
$$E(X)=\sum_{x=0}^{\infty}x\frac{\lambda^x}{(x-1)!}e^{-\lambda}$$
そして分子の\(\lambda\)だけ外に出してあげると、\(\lambda\)と、\(x\)が\(0\)から無限大のポアソン確率の和が出来上がります。
$$E(X)=\lambda\sum_{x=0}^{\infty}x\frac{\lambda^{x-1}}{(x-1)!}e^{-\lambda}$$
全ての確率の和は1であるという、確率質量関数の定義に従い、\(\lambda\)と\(1\)の積になり、期待値は\(\lambda\)です。
次は、\(E[x(x-1)]\)です。
やることは同じです。今度は、\(x\)でなく\(x(x-1)\)をかけます。
$$E(X(X-1))=\sum_{x=0}^{\infty}x(x-1)\frac{\lambda^x}{x!}e^{-\lambda}$$
約分をすると今度は、分子のλを2個だけΣの前に持ってくる必要があります(分子とXの数を合わせるため)
$$E(X(X-1))=\sum_{x=0}^{\infty}\frac{\lambda^{x-1}}{(x-2)!}e^{-\lambda}$$
よって\(\lambda^2\)と1の積になるので、答えは\(\lambda^2\)です。
(2)分散は、2乗の期待値から期待値の2乗を引いたものでした。
\(Var(X) = E[x^2] – E[x]^2\) でしたね。
第一項をよく見ると、(1)の形がうまく使えることに気が付きます。
$$E(X^2)=E(X(X-1))+E(X)$$
\(\mu = E[X]\)であることから、\(Var(X) = E[X(X-1)] + \mu -\mu^2\) は示されました。
あとは、計算するだけです。
$$Var(X)=E(X(X-1))+E(X)-E(X)^2$$
(1)より、\(\lambda^2 + \lambda – \lambda^2 = \lambda\) となる事がわかります。
よって分散も\(\lambda\)になります。
さて、ポアソン分布では平均と分散が等しいという性質がありますが、実データではこの仮定が成り立たないことがあります。
この現象をオーバーディスパージョンと呼び、その場合は負の二項回帰などの代替モデルを考慮する必要があります。
CODE
有名なポアソン分布の例を扱ってみましょう。
プロイセン騎兵連隊において1年間に馬に蹴られて死んだ兵隊の数の分布です。
| 死亡数 | 0 | 1 | 2 | 3 | 4 | 5 |
| 観測数 | 109 | 65 | 22 | 3 | 1 | 0 |
1年間に馬に蹴られて1人の兵士が死亡するという生起率\(\lambda\)が0.61と知られているとしましょう。
これは、単位あたりの平均事故数と考えていただいてokです。
from scipy.stats import poisson
import matplotlib.pyplot as plt
import numpy as np
# データの定義
deaths = [0, 1, 2, 3, 4, 5]
observations = [109, 65, 22, 3, 1, 0]
# ポアソン分布の生起率の設定
lambda_ = 0.61
# ポアソン分布に従うと仮定した場合の頻度の計算
expected_frequencies = [poisson.pmf(k, lambda_) * sum(observations) for k in deaths]
# 図示
fig, ax = plt.subplots()
ax.bar(deaths, observations, width=0.4, label='Observed', align='center')
ax.bar(np.array(deaths) + 0.4, expected_frequencies, width=0.4, label='Poisson Expected', align='center')
ax.set_xlabel('Number of Deaths')
ax.set_ylabel('Number of Occurrences')
ax.set_title('Poisson Distribution of Deaths by Horse Kicks')
ax.legend()
plt.show()
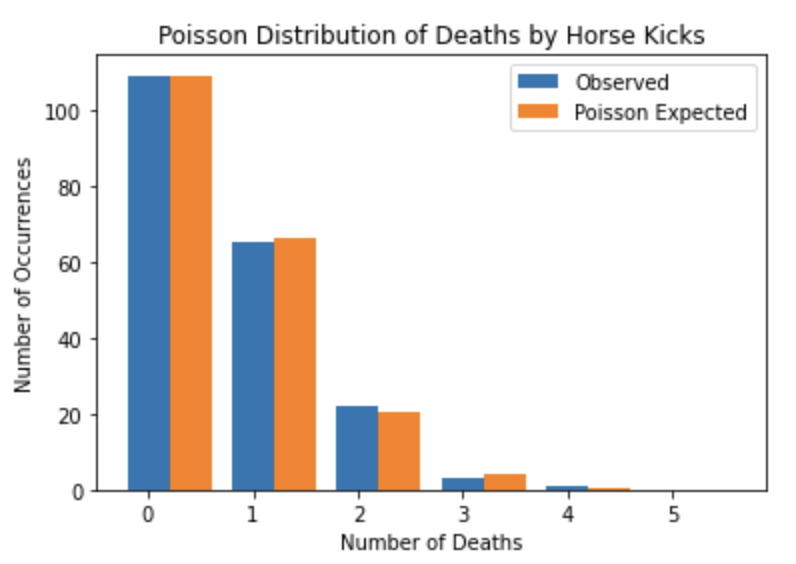
かなりポアソン分布に近いデータだということがわかりましたね!
生起率λの検定(hypothesis testing)
$$p(x)=\frac{\lambda^x}{e^{-\lambda}}$$
以上のようなポアソン分布の生起率\(\lambda\)が正の実数\(\lambda_0\)という特定の値であるという帰無仮説を立てます。
仮説
\(H_0\)(帰無仮説):\(\lambda = \lambda_0\)
\(H_1\)(対立仮説):\(\lambda > \lambda_0\)
棄却域は以下のように設定します。
$$\hat{\lambda}-\lambda_0>C$$
左辺の第1項は生起率の最尤推定量です。
以下のコンテンツで解説しましたが、生起率の最尤推定量は標本平均です。
ここで検定統計量は、以下のようになります。
分散も生起率\(\lambda\)に一致しています。
$${\frac{\hat{\lambda}-\lambda_0}{\sqrt{\lambda_0}}\sim N(0,1)}$$
この検定統計量は標準正規分布に従います。
そのほか統計的仮説検定について学習したい方は、以下のコンテンツをご覧ください。
再生性(reproductive property)
ポアソン分布には、「再生性」という嬉しい特性があります。
再生性とは、「確率変数同士を足しても、その分布がわかる」という特性です。
命題
1:\(X_1\)と\(X_2\)は独立
2:\(X_1\) ~ \(Po(\lambda_1)\)
3:\(X_2\) ~ \(Po(\lambda_2)\)
ならば、\(X_1 + X_2\) ~ \(Po(\lambda_1 + \lambda_2)\)が成り立つ。
つまり、\(X_1\)と\(X_2\)という独立した確率変数がそれぞれポアソン分布に従っている場合には、その確率変数の和自体も、生起率を\((\lambda_1+\lambda_2)\)とするポアソン分布に従います。
もっと汎用的な話としては、以下のようになります。
${X_1,X_2,‥,X_n \sim Po(\lambda)}$で独立かつ同一の分布に従うとき、
$${W_n = X_1 + X_2 + ‥ + X_n ~ Po(n\lambda) }$$
和の分布も当然ポアソン分布に従います。
生起率は\(n\lambda\)です。

では、再生性があると何が嬉しいのかというと、標本平均の分布が正確にわかるということが挙げられます。
$$P(\overline{X}=\frac{k}{n})=P(W_n=k)=\frac{(n\lambda)^k}{k!}e^{-n\lambda}$$
標本平均が\(\frac{k}{n}\)になるという確率は、和が\(k\)になるという確率と同じです。
あとは、ポアソン分布の分布関数を用いると答えが求められる、という話です。
ちなみにベルヌーイ分布や正規分布にも再生性はありますので、確率変数同士を足しても分布がわかります。
詳しくは、WEB版青の統計学の記事をご覧ください。
一般線形モデルを学習したい方やポアソン分布の最尤推定量を知りたい方は以下のコンテンツをご覧ください。
補足|ポアソンの極限定理と二項分布
ちなみにポアソン分布は、二項分布の極限としても現れます。
具体的には、試行回数nが大きく\(n→\infty\)、成功確率pが小さいとき\(p→0\)、二項分布\(Bin(n, p)\)はポアソン分布\(Po(np)\)に近づきます。
これは「ポアソンの極限定理」として知られています。
$$\lim_{{n \to \infty, p \to 0}} P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!}$$
二項分布の試行回数\(n\)と成功確率\(p\)の積、\(np\)が強度\(λ\)に等しいので
$$np=\lambda,p=\frac{\lambda}{n}$$
二項分布の確率質量関数である、\(P(X=x)={}_nC_xp^x(1-p)^{n-x}\)に代入してみます。
$$=\frac{n!}{x!(n-x)!} (\frac{\lambda}{n})^x(1-\frac{\lambda}{n})^{n-x}$$
\((1-\frac{\lambda}{n})^{n-x}\)をn乗の部分と\(-x\)乗の部分にわけて、あげると以下のように変形できます。
$$=\frac{1}{x!} (1-\frac{1}{n})…(1-\frac{x-1}{n})λ^x (1-\frac{λ}{n})^n(1-\frac{λ}{n})^{-x}$$
ここで、\(n\)を\(\infty\)に近づけると、\((1-\frac{\lambda}{n})^n\)以外は\(1-0\)の形になり、積としては1をかけるだけになります。そしてネイピア数の公式より以下のようなことが言えます。
$$\lim_{n\to \infty} (1-\frac{\lambda}{n})^{n}=\lim_{n\to \infty}(1-\frac{λ}{n})^{{-\frac{n}{\lambda}}^{-\lambda}}=e^{-\lambda}$$
よって、残ったものは\(e^{-\lambda}\frac{\lambda^{x}}{x!} \)となり、ポアソン分布の確率質量関数と一致しますね。








