【統計検定2級で頻出】歪度と尖度を実例を通して解説|python
こんにちは、青の統計学です。
今回は尖度と歪度という2つの統計量をみてみましょう。
Rとpythonどちらのコードも用意してあります。
歪度/skewness
$$\frac{E[(x-μ)^3]}{σ^3}$$
統計検定で最低限必要な知識としては、
・右裾が長い、あるいは左に偏った分布の時には正の値をとる
・左裾が長い、あるいは右に偏った分布の時には負の値をとる
・正規分布では0の値をとる。
・多峰だからといって0にはならない。
という事です。
CODE|R
x <- c(6.0,10.0,7.6,3.5,1.4,2.5,5.6,3.0,2.2,5.0,3.3,7.6,5.8,6.7,2.8,4.8,6.3,5.3,5.4,3.3,3.4,3.8,3.3,5.7,6.3,8.4,4.6,2.8,7.9,8.9)
hist(x)xに、以上のようなデータを入れてみましょう。値はなんでもいいです。
ヒストグラムをかいてみましょう。
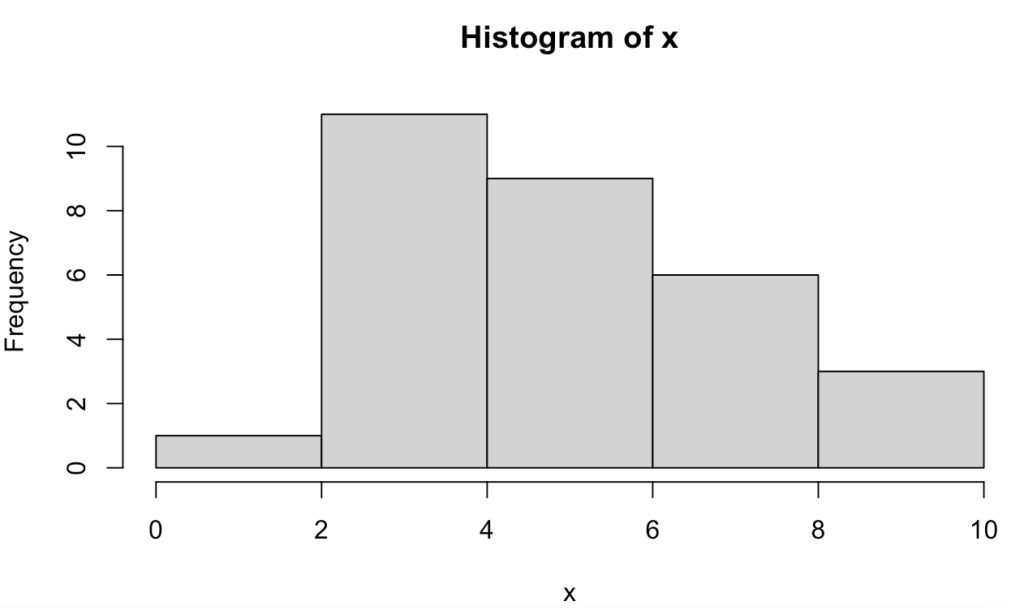
こんな感じになりました。明らかに左右対称ではありません。どちらかというと「右裾が長いので正の値」をとりそうです。
skewness(x)これは歪度を求めるコマンドです。実行すると0.3614441と出力されました。
尖度(kurtosis)
$$\frac{(x-μ)^4}{σ^4}$$
偏差の4乗の期待値を標準偏差の4乗で割った数が尖度になります。
統計検定2級の問題では、この値から-3されたものが尖度と定義されています。
統計検定で最低限必要な知識は、
・正規分布よりも尖っていれば正の値を取る
・正規分布よりも扁平ならば負の値を取る
という事です。
CODE|R
先ほどと同じデータを使ってみましょう。
x <- c(6.0,10.0,7.6,3.5,1.4,2.5,5.6,3.0,2.2,5.0, 3.3,7.6,5.8,6.7,2.8,4.8,6.3,5.3,5.4,3.3, 3.4,3.8,3.3,5.7,6.3,8.4,4.6,2.8,7.9,8.9)
kurtosis(x)尖度を求めるコマンドです。-0.8275311と出力されました。正規分布よりも結構扁平という事ですね。
CODE|python
Pythonでは、NumPyを使うことで、簡単に尖度と歪度を求めることができます。
以下は、尖度と歪度を求める例です。
import numpy as np
# 標本データ
data = [1, 2, 3, 4, 5, 6, 7, 8, 9]
# 尖度
skewness = np.mean((data - np.mean(data))**3)/np.std(data)**3
# 歪度
kurtosis = np.mean((data - np.mean(data))**4)/np.std(data)**4
print("Skewness: ", skewness)
print("Kurtosis: ", kurtosis)
ここまで、歪度と尖度について紹介してきました。では、例題を解いてみましょう。
一様分布U(-1,1)の歪度と尖度を求めてみましょう。
【解説】まずは、一様分布U(-1,1)の期待値と分散を求める必要があります。
一様分布U(a,b)の確率分布関数は、f(x) = 1/(b – a) です。
期待値は、(a+b)/2 となります。これは、データが一様に分布しているためわかりやすかもしれません。
分散は、期待値がわかれば計算できますね。「2乗の平均から平均の2乗を引く」と、出てきます。
よって(b-a)^2/12 となります。
実際の問題は、U(-1,1)なので、a=-1,b=1ですね。よって確率分布関数f(x)は1/2で、期待値μは0で、分散σ2は1/3となります。
まず歪度を求めてみましょう。
$$ \frac{E[(x-μ)^3]}{σ^3} = \frac{E[(X-0)^3]}{σ^3} = \frac{\displaystyle \int_{-1}^{1}x^3f(x)dx}{σ^3}$$
Xの範囲は-1から1であることに注目しましょう。
分子は0なので、歪度は0です。左右対称な確率分布であることがわかりました。
次に尖度を求めてみましょう。
$$ \frac{E[(x-μ)^4]}{σ^4} = \frac{E[(X-0)^4]}{σ^4} = \frac{\displaystyle \int_{-1}^{1}f(x)dx}{σ^4}$$
ここからは省略しますが、答えは9/5です。
今回分子は1/5です。分母のσ^4は分散の2乗なので分母は1/9です。
モーメント(moment)
単回帰分析や重回帰分析の最小二乗法の前提として、「4次までのモーメントがある」という仮定を見たことがあると思います。
これは「異常値がない」という解釈になるのですが、「モーメント」と聞いてよくわからない方も多いと思います。
モーメントは、歪度と尖度に大きく関わりますので、この機会に学んでおきましょう。
まずは、関数f(x)の期待値を求めてみます。f(X)=x^kとすると、
$$E[f(x)]=E[x^k]= \sum_{i=0}^Nx_{I}^kp_{i}$$
これを、k次モーメントと呼びます。pは確率ですね
つまり、k=1の時は1次モーメントとなり、期待値と一致します。
平均回りのモーメント
次にg(x)を、xから平均を除いた偏差のk乗として扱います。また期待値の形にしましょう。
$$E[g(x)]=E[(x-μ_{X})^k]= \sum_{i=0}^N(x_{I}-μ_{X})^kp_{i}$$
これを平均回りのk次モーメントと呼びます。
k=2の平均回りのモーメントは、値のばらつきを表す「分散」と呼びます。
k=3の平均回りのモーメントは、正規分布と比べて分布の非対称度を表す「歪度」に使われます。
$$ \frac{E[(x-μ_{X})^3]}{σ^3}$$
k=4の平均回りのモーメントは、平均から大きく離れた値の出やすさを表す「尖度」に使われます。
$$ \frac{E[(x-μ_{X})^4]}{σ^4}$$
また、「モーメント」は統計検定準一級で扱われる「積率母関数」で使う重要な概念になります。
覚えておいて損はないと思います。
モーメント法含め、積率母関数についてもっと詳しく学習したい方は、【期待値の応用】モーメント法とモーメント母関数(積率母関数)についてをご覧ください。
統計検定のチートシートは以下をクリック!
【最短合格】統計検定準一級のチートシート|難易度や出題範囲について
【最短】統計検定2級合格ロードマップとチートシート|おすすめの本について

