【t検定】t統計量(t値)の求め方

統計検定2級の後半で頻出の「t統計量」についてご説明します。

標準誤差を知っておく必要があるので、標準誤差を知らない方は、【Standard Error】標準誤差を例題を通して解説。をご覧ください。

t統計量

例題1

サンプル数100のデータで、$y=β0 + β1(car) + β2(truck) + u_i$を考えます。

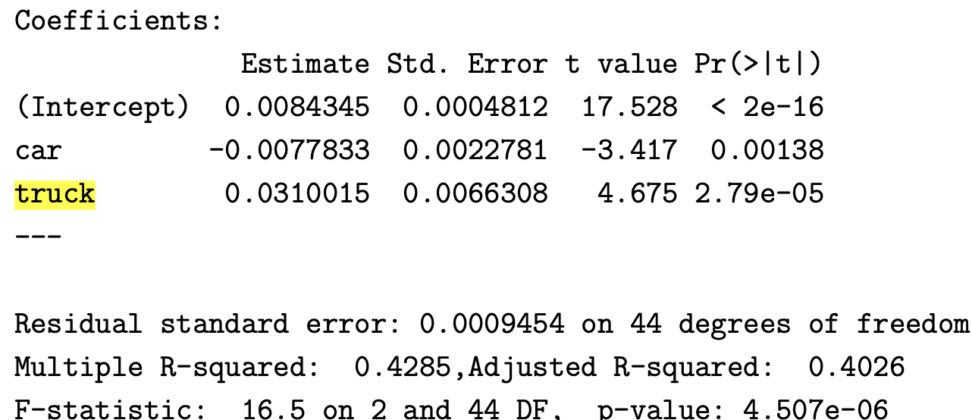
有意水準5%で有意になる係数を全て選びましょう。

解説1

まずt値のことを理解しましょう。

t値(t value)とは

t検定で使う検定統計量のことです。以下のような式で求められます。

$$t \quad value = \frac{\hat{β}_1 – β_{1}}{SE(\hat{β}_1)}$$

標準誤差で真の値と推定量の差を割っています。

推定誤差の大きさで調整しているという意味から、各説明変数を公平に比較し、計算された回帰係数が0から離れているかを確認するための指標です。

例としてβ0を挙げましたが、他も同じです。

上の表を見ていただければ、t値と推定値(estimate)と標準誤差(Std error)がわかります。

t valueが17.528の定数(intercept)と、4.675のtruckの係数が有意です。

また、標準誤差とは標準偏差をサンプル数の平方根で割った値です。

$$SE = \sqrt{\frac{\hat{σ}^2}{n}}$$

この時のt統計量は、自由度(サンプル数-定数項含めた変数の数-1)のt分布に従います。

上の例でいうと、100-3-1=96が自由度になります。

ちなみに、係数推定値の共分散行列の対角要素は各係数の推定値の分散を表し、その平方根を取ると、それぞれの係数の標準誤差になります。

なお、標準誤差とは、推定値の標準偏差のことを指します。

よって、対角要素の値が大きいほど、その回帰係数の推定値の不確定性（またはばらつき）が大きく、標準誤差も大きくなります。

そして標準誤差が大きいほど、推定値が真の値からどの程度離れる可能性があるか、という指標も大きくなります。

標準誤差に関して学びたい方は以下をご覧ください。

【Standard Error】標準誤差を例題を通して解説

t検定について

一様分布から発生させた乱数が95%信頼区間にいるカバレッジ確率(範囲に値が入る確率)を考えてみましょう。

当然一様に乱数は分布するので確率はnが大きいほど0.95に近づきます。

$$\overline{x}- \frac{V}{\sqrt{n}}Z_{α/2}<p<\overline{x}+ \frac{V}{\sqrt{n}}Z_{α/2}$$

正規分布でもなく、分散もわからないので、t検定を使います。

CODE

S = 10000
#試行回数

n = 100
#サンプル数

res = rep(NA,S)
#S個だけ入るベクトルを作る

a = 0.05
#信頼区間

Z = - qnorm(a/2)
#下側検定への変換

for(i in 1:10000){
  x = runif(n)
  #n個のデータを入れる
  
  m=mean(x)
  V2 = var(x)
  #不偏分散
  V = sqrt(V2)
  
  L = m - Z*V/sqrt(n)
  #下限
  U = m + Z*V/sqrt(n)
  #上限
  
  res[i] = L < 0.5 && 0.5 < U
  #ベクトルを保存する
  
}
mean(res)
#カバレッジに成功した割合

サンプルが100の実験を10000回繰り返しましょう。rep(NA,S)には、事前に10000個入るベクトルを用意しておきます。

qnorm(a/2)は、指定した下側確率に対応するｚ値（境界値)です。

xには、runif(n)には一様分布からn個の乱数を発生させます。var(x)は不偏分散を出すのでご注意ください。

> mean(res)
[1] 0.9512

0.95にかなり近い値が出ました。nを大きくするほど0.95に近づきます。

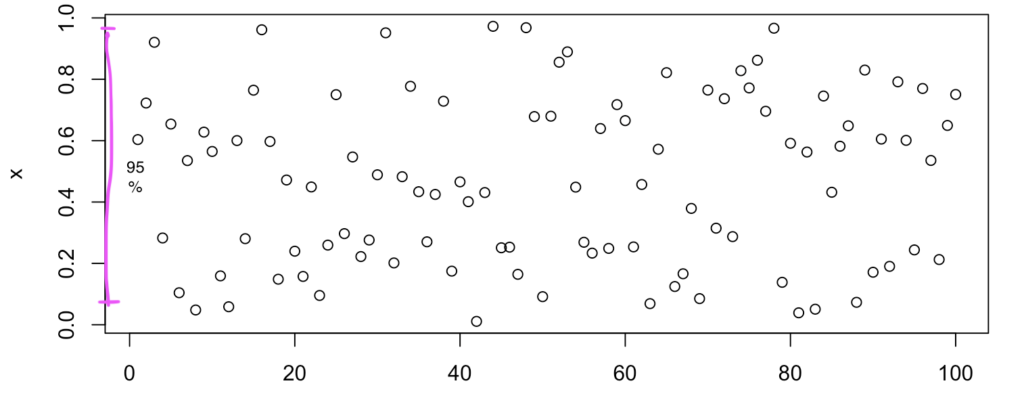
上の図は一様分布から乱数を出してプロットしたものです。ピンクの範囲に95個入ってると望ましいです。

例題2

重さμの製品を検品します。サンプル数n=16、標本平均3.950で、重さX1‥Xn i.i.d〜N(μ,σ^2)です。母分散はわからないものとします。

不偏分散は0.1とします。この時のμの95%信頼区間を作りましょう。

解説

正規分布かつ分散未知の場合は、t分布を使います

$$\overline{x}- \frac{V}{\sqrt{n}}t_{α/2}<p<\overline{x}+ \frac{V}{\sqrt{n}}t_{α/2}$$

t分布には自由度が必要です。自由度は、サンプル数-1です。よって15です。

	α=0.1	α=0.05	α=0.025	α=0.01	α=0.005
1	3.078	6.314	12.706	31.821	63.657
2	1.886	2.920	4.303	6.965	9.925
3	1.638	2.353	3.182	4.541	5.841
4	1.533	2.132	2.776	3.747	4.604
5	1.476	2.015	2.571	3.365	4.032
6	1.440	1.943	2.447	3.143	3.707
7	1.415	1.895	2.365	2.998	3.499
8	1.397	1.860	2.306	2.896	3.355
9	1.383	1.833	2.262	2.821	3.250
10	1.372	1.812	2.228	2.764	3.169
11	1.363	1.796	2.201	2.718	3.106
12	1.356	1.782	2.179	2.681	3.055
13	1.350	1.771	2.160	2.650	3.012
14	1.345	1.761	2.145	2.624	2.977
15	1.341	1.753	2.131	2.602	2.947
16	1.337	1.746	2.120	2.583	2.921